 |
Главная |
Функции распределения частиц. Функция Ферми-Дирака
|
из
5.00
|
Функцией распределения в статистической теории принято называть функцию, которая в условиях термодинамического равновесия при заданной температуре Т пропорциональна вероятности того, что некоторая частица занимает определенный энергетический уровень Е.
Вид функции распределения зависит от возможного количества частиц в данном разрешенном энергетическом состоянии и от того, являются ли данные частицы различимыми. Различимость – это свойство частиц изменять физические характеристики твердого тела при перестановке частиц местами.
В классической физике частицы считаются различимыми и могут неограниченно заполнять одно и то же энергетическое состояние. Распределение частиц газа по энергиям описывается с помощью функции распределения Максвелла - Больцмана:
 ;
;  (2.32)
(2.32)
где μ – химический потенциал, выражающий изменение свободной энергии системы при изменении числа частиц в системе на одну при постоянной температуре и постоянном объеме системы:  (фактически – работа выхода); С – постоянная, которая находится из условия, что сумма частиц на всех уровнях системы равна некоторому заданному и неизменному числу N. Название химический потенциал, а не какой–либо другой, подчеркивает лишь то обстоятельство, что рассматриваемые частицы способны двигаться по законам механики.
(фактически – работа выхода); С – постоянная, которая находится из условия, что сумма частиц на всех уровнях системы равна некоторому заданному и неизменному числу N. Название химический потенциал, а не какой–либо другой, подчеркивает лишь то обстоятельство, что рассматриваемые частицы способны двигаться по законам механики.

В отличие от классических представлений в квантовой механике микрочастицы являются неразличимыми. Микрочастицы подразделяются на 2 группы: бозоны и фермионы. Бозоны могут неограниченно заполнять одно и то же энергетическое состояние, причем тем легче, чем больше их в этом состоянии находится. Фермионы подчиняются запрету Паули. Это значит, что одно квантовое состояние может быть занято не более чем одним фермионом.
К бозонам относятся: фотоны, фононы, пионы, а к фермионам - электроны, протоны, нейтроны.
Бозоны подчиняются статистике Бозе-Эйнштейна
 (2.33)
(2.33)
В условиях равновесия бозоны имеют минимум свободной энергии, поэтому химический потенциал бозонов равен нулю. Отсюда следует
 (2.33А)
(2.33А)
Распределение фермионов по энергетическим уровням описывается с помощью функции Ферми-Дирака:
 (2.34)
(2.34)
где k – постоянная Больцмана, Т – температура, EF – энергия Ферми или электрохимический потенциал, т.е. работа, которую необходимо затратить для изменения числа частиц на одну единицу. В случае, когда частицами, составляющими статистическую систему, являются электроны, которые помимо массы обладают еще и электрическим зарядом, изменение энергии возможно за счет изменения заряда. Электрохимический потенциал, который представляет собой алгебраическую сумму химического и электростатического потенциалов, то есть равен (EF=μ-ej), где j - электростатический потенциал, и отражает это. Обычно его отождествляют с уровнем (энергией) Ферми. Можно показать, что в условиях термодинамического равновесия энергия Ферми оказывается постоянной в любой системе контактирующих тел. Поэтому необходимым условием равновесия системы можно считать постоянство уровня Ферми.
Характерно, что вид функции Ферми-Дирака не зависит от свойств системы, а зависит только от температуры. Конкретные свойства системы отражаются лишь на положении уровня Ферми. Графическое изображение функции распределения Ферми-Дирака представлено на рис. 2.4.
Основные свойства функции Ферми-Дирака.
-
 , т.е. уровень Ферми занят с вероятностью 0,5 (всегда!).
, т.е. уровень Ферми занят с вероятностью 0,5 (всегда!).
То есть уровень Ферми есть энергетический уровень, вероятность заполнения которого при температуре, отличной от абсолютного нуля равна 0.5.
-
 К. Тогда:
К. Тогда: 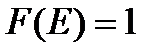 для
для 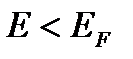 и
и  для
для  ,
,
т.е. при температуре  К все разрешенные состояния ниже уровня Ферми заняты, а все выше него – полностью свободны. Это отличается от случая классических частиц, когда при
К все разрешенные состояния ниже уровня Ферми заняты, а все выше него – полностью свободны. Это отличается от случая классических частиц, когда при  К все электроны имеют
К все электроны имеют 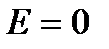 .
.
Следовательно, энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля.
- Если энергия электронов значительно выше энергии Ферми, т.е.
 , тогда
, тогда
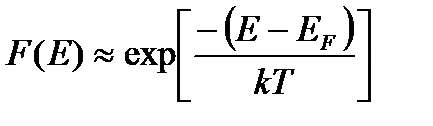 . (2.35)
. (2.35)
Формула (2.35) представляет собой классическое распределение Максвелла-Больцмана. Таким образом, функция Ферми-Дирака при больших энергиях переходит в распределение Максвелла-Больцмана.
- Если энергия электрона ниже ЕF настолько, что
 , тогда:
, тогда:
 , (2.36)
, (2.36)
т.е. в области энергий, существенно меньших  , разрешенные состояния заняты с вероятностью, близкой к 1.
, разрешенные состояния заняты с вероятностью, близкой к 1.
5. В области 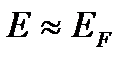 функция
функция  изменяется очень быстро от значений, близких к 1, до нуля. Скорость изменения зависит от
изменяется очень быстро от значений, близких к 1, до нуля. Скорость изменения зависит от  , и для температуры абсолютного нуля равна бесконечности (рис.2.4 в).
, и для температуры абсолютного нуля равна бесконечности (рис.2.4 в).
Функция распределения Ферми-Дирака (2.34) характеризует вероятность заполнения данного состояния электроном. Вероятность того, что в состоянии с энергией Е электрон отсутствует, т.е. оно занято дыркой, будет равна:
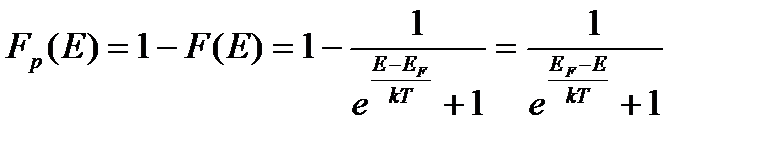 (2.37)
(2.37)
Следовательно, функция распределения для дырок аналогична функции распределения для электронов, если отсчитывать энергию дырок от уровня Ферми в противоположную сторону по сравнению с направлением отсчета энергии для электрона.
 (а)
(а)
| |
 (в) (в)
| |
| Рис. 2.4. Распределение Ферми-Дирака. |
При Т>0 часть электронов за счет теплового движения смогут перейти в состояние с E>EF. Число частиц, перешедших на более высокие уровни, равно количеству образовавшихся свободных состояний в области Е<EF. Это означает, что заштрихованные на рис. 2.4 (б) площади равны. Кроме этого, нетрудно заметить, что величина F(E) заметно отличается от 1 или 0 лишь в пределах нескольких (~3)  вблизи значения E=EF (рис.2.4 в). Из рисунка видно, что функция Ферми-Дирака испытывает сильное изменение от 0,953 до 0,047 при изменении
вблизи значения E=EF (рис.2.4 в). Из рисунка видно, что функция Ферми-Дирака испытывает сильное изменение от 0,953 до 0,047 при изменении  в интервале от –2kT до +2kT. В дополнение хорошо видно, что интервал энергии, определяющий резкое изменение F(E,Т), зависит от температуры: при Т ® 0 он стремится к нулю.
в интервале от –2kT до +2kT. В дополнение хорошо видно, что интервал энергии, определяющий резкое изменение F(E,Т), зависит от температуры: при Т ® 0 он стремится к нулю.
Полупроводники, у которых распределение свободных носителей заряда по энергетическим состояниям описывается функцией Ферми-Дирака, называются вырожденными. Вырожденными являются такие полупроводники, у которых уровень Ферми расположен вблизи края запрещенной зоны (как правило, на расстоянии менее нескольких kT).
Для электронов, находящихся в состояниях с энергией E-EF>>  , выражение для F(E) принимает вид:
, выражение для F(E) принимает вид:
 , (2.38)
, (2.38)
то есть совпадает с функцией распределения Максвелла-Больцмана для частиц, подчиняющихся классическим законам.
Если распределение носителей заряда по энергиям в полупроводнике подчиняются статистике Больцмана, то полупроводник называют невырожденными.
Невырожденными являются такие полупроводники, у которых уровень Ферми расположен внутри запрещенной зоны на расстоянии более нескольких kT от границы с разрешенной зоной.
|
из
5.00
|
Обсуждение в статье: Функции распределения частиц. Функция Ферми-Дирака |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

