Разведочная гравиметрия

Горные породы различаются между собой по плотности. Это одна из наиболее информативных их физических характеристик. Плотность горных пород, являющаяся функцией пространственных координат, зависит от химического состава и фазового состояния вещества, напряжения и температуры. Частично эти параметры отражают историю формирования вещества – частично определены процессами, происходившими в последующем развитии объектов, в которых это вещество участвовало, частично современными условиями и происходящими процессами. Таким образом, знание плотностных свойств горных пород позволяет не только делать заключения о генезисе изучаемых объектов, но и изучать процессы, происходившие в Земле. Однако, что самое главное для задач прикладного характера, информация о плотности - важнейшая компонента данных для принятия решений о наличии и характере распределения полезных ископаемых. В этой связи реконструируемая плотностная модель среды, во-первых, позволяет изучать характерные черны геометрической модели геологического объекта, во вторых, получить информацию о ее динамической модели и, тем самым, обеспечить прогнозирование перспективных площадей на детальный поиск и разведку месторождений. Наконец, по значениям плотности возможен собственно прогноз зон, перспективных на наличие полезных ископаемых. Совокупность тех зависимостей, которые предопределяют значения плотности по параметрам геологической модели (возраст, динамо-тектонические условия, условия метаморфизма) через перечисленные выше химические параметры, параметры фазового состояния (пористость, как отношение объемов твердой фазы к остальным, характер флюидонасыщения, соотношение объемов различных флюидов и т.д.), параметры температурного режима определяют геолого-геофизические связи. Эти же факторы предопределяют и другие физические свойства, такие как скорость распространения упругих волн, магнитную восприимчивость, теплопроводность, электрические свойства. Плотность горных пород оказывается связанной с перечисленными и многими другими физическими параметрами, чем определена взаимосвязь между ними. В силу сложности эти взаимосвязи носят экспериментальный и по этой причине локальный характер. Однако их наличие – объективный фактор, делающий плотностную модель среды одной из наиболее информативной для обеспечения геологической интерпретации – реконструкции геологической модели.

Изучение плотностных неоднородностей в Земной коре составляет предмет разведочной гравиметрии. Локальные неоднородности распределения масс в Земной коре вызывают гравитационные аномалии. Регистрируя их, можно ставить задачу нахождения этих плотностных неоднородностей.

2.1.1 Плотностная (физическая) модельгеологической среды представляет собой функцию, значение которой в каждой точке равно плотности геологической среды в этой точке. Плотность измеряется в г/см³ . Однако изучать абсолютные значения плотности неудобно, поскольку в этом случае придется рассматривать всю Землю целиком. В этой связи предполагается, что имеется некоторая фоновая плотность , характерная для всей среды вне изучаемого объема. Отличия от фонового значения наблюдаются только в этом объеме. Эти отличия, представляющие собой разность между значениями плотности в точках изучаемого объема и фоновым значением плотности, и есть изучаемая плотностная неоднородность. Для ее описания введем прямоугольную систему координат XYZ, расположив плоскость XOY касательно к дневной поверхности и направив ось OZ вниз к массам (Рис. 2.1).

Пусть V – область, целиком лежащая в нижнем полупространстве E_(z>0), в пределах которой сконцентрированы изучаемые плотностные неоднородности. Синонимом плотностной неоднородности служит аномальная плотность σ, т.е. разность между значением плотности модели и плотностью , рассматриваемой как плотность вмещающей объем V среды (она принимается постоянной). Значения аномальной плотности свои для каждой точки пространства и представимы как функция координат . Физически очевидные предположения относительно свойств этой функции таковы – она ограничена, имеет только конечное число поверхностей, вдоль которых есть разрывы первого рода. Если область V ограничена, то этого достаточно, чтобы можно было рассматривать эту функцию как элемент любого из пространств . В том же случае, если область V неограниченна, например, представляет собой бесконечную горизонтальную полосу, ограниченную двумя значениями глубин по вертикали ( ), то для принадлежности введенной плотностной модели функциональному пространству 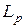, следует вести соответствующие условия интегрируемости, что, однако, не имеет никаких ощутимых физических следствий. Таким образом, параметризацией плотностной модели служит некоторое пространство функций. Обозначим его X. Это, в частности, может быть пространство функций интегрируемых в области с заданной степенью ( ). Несмотря на общность введенной физической модели среды, она все же содержит ряд существенных ограничений. Сюда относится, например, предложение об отсутствии аномальных масс вне области V, рассмотрение плотности как изолированного физического параметра вне связи с другими, наконец, предположение о том, что все массы расположены в нижнем полупространстве.

Из приведенной модели среды достаточно легко построить множество других – частных по вводимой параметризации, используя принцип проектирования

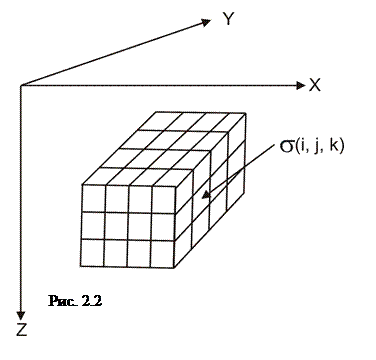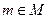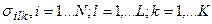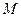Пусть M некоторая аппроксимационная модель, и m ее элементы. Например, в качестве M выступает сетка, разбивающая область V – прямоугольную призму в E_, на ячейки числом . Элементом , служит множество значений плотности в ячейках сетки . Это новая параметризация, параметрами которой служат величины . Основываясь на , легко построить ее подмножества следующим приемом. Определим оператор проектирования произвольного плотностного распределения из X на 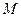правилом:

(2.1)

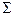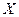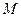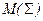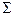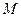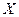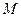Если пробегает множество элементов из , то соответствующие проекции образуют некоторое подмножество в . Оно обозначается . Следовательно, образом многообразия при проектировании на в норме пространства служит . Это подмножество в . В приведенном определении пространство X «работает» как множество, которому принадлежат все рассматриваемые элементы, но самое важное то, по какому правилу вычисляется норма в определении оператора проектирования. Если из контекста ясно, о какой норме идет речь, то этот символ в (1) опускаем.

Моделью физического поля служит вертикальная производная гравитационного потенциала 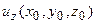, заданного в точке x₀,y₀,z_0, находящейся вне области V. Исходя из закона тяготения, она рассчитывается по формуле:

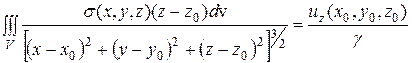. (2.2)

γ – гравитационная постоянная.

Это пример. В качестве модели физического поля может быть с равным успехом взята любая комбинация производных любого порядка от (2) по переменным . Выражение (2) более предпочтительней лишь по той причине, что при некоторых допущениях, в частности, предположении, что направление нормали к Земле совпадает с вертикальной координатой, 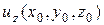ассоциируется с наиболее часто используемой и измеряемой аномалией силы тяжести 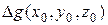.Соотношение (2) либо ему аналогичное сокращенно будем записывать:

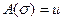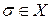. . Для произвольной модели 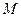, можно записать: или:

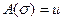
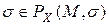
(2.3)

Прямым вычислением легко проверяется, что функция 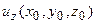в (2) является гармонической всюду вне области 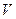удовлетворяет уравнению Лапласа:

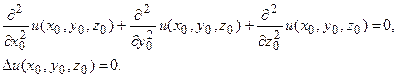
Внутри этой области она удовлетворяет уравнению Пуассона:

.

Поскольку вне области 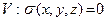то уравнение Пуассона автоматически переходит в уравнение Лапласа.

Структурная модель

Частный случай – структурно-плотностная модельсреды . Это геометрическая плотностная модель, параметрами которой служат конфигурации плотностных границ. Она схематично изображена на рис.3.

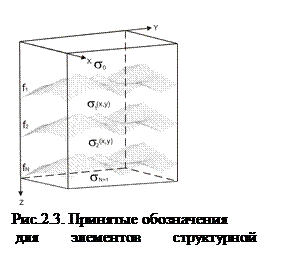В горизонтальной полосе П, ограниченной в области вертикальными координатами расположено N слоев, ограниченных N+1 плотностной границей. Каждый слой имеет плотность, которая известна и может быть переменной по латерали, за исключением плотности s_N+1 слоя, лежащего ниже последней границы (номер N). Эта плотность считается известной, постоянной и равной введенной ранее фоновой плотности. Границы, ограничивающие пласты, представляют собой однозначные функции пространственных координат. Вне некоторой цилиндрической области V, горизонтальное основание которой (проекция на плоскость E₀) есть S, а боковая поверхность - D, границы выходят на асимптоты. Точный смысл понятию асимптот в данных модельных представлениях можно придать следующим предположением. Плотность вне V постоянна вдоль каждого луча, выходящего из любой точки на D ортогонально этой поверхности. Главным предметом изучения в этой модели служат плотностные границы. Влияние объектов вне области V учитывается соответствующими процедурами редуцирования. В частности асимптотическое поведение границ вне D рассчитывается и их гравитационное влияние моделируется. Будем считать, что плотностные границы описываются функциями 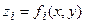, i=0,1,..N, и плотность пласта, заключенного между границей с номером i-1 и границей с номером i, есть (здесь i меняется от 1 до N). В связи с тем, что в практике интерпретации гравитационных полей принято работать с аномальными эффектами и избыточными (относительно некоторого уровня) плотностями, можно считать, что плотность объектов ниже границы с номером N равна нулю, что означает s_N+1=0. Это означает, что все плотности посчитаны в отношении к плотности нижележащей среды. Кроме того, считаем, что 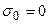, что является идеализацией. На практике эти условия легко обходятся введением дополнительной верхней и нижней горизонтальных границ на глубинах z₁ и z₂ , с соответствующими процедурами редуцирования. В приведенных представлениях о строении среды связь между вертикальной производной гравитационного потенциала и параметрами модели среды в области V легко получается расстановкой пределов интегрирования в (2):

Интегрируя последнее выражение и расставляя пределы интегрирования, получим:

Перегруппировав суммирование, легко получим:

(2.4)

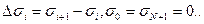
Соотношение (4) типичный пример записи общего выражения (3) для введенной геометрической плотностной модели среды. В силу его особой значимости для него вводится специальное обозначение:

,подчеркивающее геометрический характер модели и наличие границ как основных параметров модели.

Соотношения (2 - 4) представляют собой уравнения связи между вводимыми параметризациями плотностной модели среды и моделью поля. На основе этих соотношений могут быть получены другие уравнения связей с другими моделями поля. Так, например, могут быть построены уравнения, связывающие плотностные модели среды и величины полного нормированного градиента в области вне источников поля, либо высшими производными гравитационного потенциала. Эти соотношения представляют собой существенные идеализации и поэтому имеют дополнительное специальное название - операторы прямой задачи – общее название решений соответствующих уравнений математической физики. В частности, (1)- операторы прямой задачи гравиразведки в классе распределений плотности, а (4) – в классе плотностных границ. Чтобы эти соотношения включить в интерпретационный процесс, необходимо от них перейти к наблюдаемым. Этот этап, в соответствии с интерпретационной моделью, соответствует эталонирующим преобразованиям. Они состоят, в частности, в учете влияния масс, расположенных вне области V, включая гравитационное влияние асимптотически продолженных границ, ненулевых значения плотносте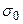й и 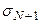в структурной модели, вообще говоря, несовпадение вертикальной и нормальной составляющих поля, влияние многих и многих других факторов, изучаемых в курсе «Гравиразведка». После того как с наблюдаемыми выполнены процедуры обработки и найдены соответствующие физические поля – правые части в (3) , в частности в (4), можно ставить задачу реконструкции физической модели по найденной модели физического поля. Это суть постановка обратной задачидля соответствующего уравнения математической физики. Ее формальная запись такова – по заданному u и уравнению (3) необходимо реконструировать 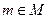так, чтобы выполнялось условие:

,

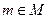
(2.5)

Запись (5), равно как чаще всего ей эквивалентную (3) следует рассматривать как формальную. Прежде всего, ниоткуда не следует, что для данного конкретного 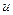ее решение существует. Наоборот, чаще всего, решения этой задачи как раз-то и не существует. Это связано с целой серией фактов. Во-первых, в процессе построения модели физического поля из наблюдаемых неизбежно допускались ошибки, которые могли «вывести результат» за пределы области допустимого. Во-вторых, при создании аппроксимационной модели легко можно было «не угадать», так что реальное распределение «лежит где то в стороне» от сконструированного модельного класса. Наконец, сами наблюдаемые осложнены ошибками. Все это означает, что на 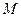просто не окажется элемента строго удовлетворяющего (5). Может оказаться, что такого элемента не существует и с заданной точностью, хотя наилучший в определенном смысле конечно существует. Но вслед за этим возникает и другой вопрос. Если этот наилучший существует, то один ли он, и какое отношение имеет к реальности? Это очень непростые вопросы, требующие специального предметного рассмотрения. Очень важно то, что эти вопросы внеметодные – они общие для обратных задач во многих их постановках и для различных геофизических методов. При этом именно в геофизике, в отличие от общих методов интерпретации физического эксперимента, они имеют особо актуальное значение и своеобразное звучание.