 |
Главная |
Тема 10.4. Сравнительная оценка параметров эмпирического и нормального распределений. Критерий Пирсона «хи» квадрат
|
из
5.00
|
Нормальный характер распределения свидетельствует о количественной однородности статистических данных и об отсутствии каких-либо причин существенным образом определяющих вариацию изучаемого явления.
Поэтому статистический анализ нередко начинается с проверки того, как фактически (эмпирически) данные ложатся на идеальную теоретическую кривую или аппроксимируются. То есть сравниваются эмпирические и теоретические данные какой-либо кривой. Это производится путем оценки гипотезы нормального характера распределения. Вероятностные статистические предположения выдвигаются в виде нулевой гипотезы. Отклонения эмпирических данных от «нормальных» носят случайный характер. Оценку нулевой гипотезы в данном случае осуществляют графическим методом или путем расчета специальных обобщающих показателей сходства, называемых критериями согласия.
Независимо от выбранного метода генеральные ряды распределения преобразуются в дискретные и стандартизируются.
Пример: Известно, что среднемесячная заработная плата всех рабочих 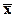 =1402,42 руб., среднеквадратическое отклонение
=1402,42 руб., среднеквадратическое отклонение 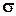 =338,58 руб.
=338,58 руб.
Данные распределения среднемесячной заработной платы:
| Средне-месячная заработная плата | Число раб-ков, 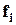 (эмпир.) (эмпир.)
| 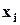
| 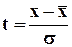
| 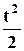
| 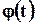
| 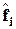 (теор.)
(теор.)
| 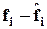
| 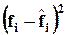
| 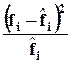
|
| До 700 | -2,37 | -2,81 | 0,0241 | 12,93 | 3,07 | 9,41 | 0,73 | ||
| 700,1-900 | -1,78 | -1,58 | 0,0819 | 44,04 | 11,96 | 142,95 | 0,73 | ||
| 900,1-1100 | -1,19 | -0,71 | 0,1969 | 105,82 | -16,82 | 282,90 | 3,25 | ||
| 1100,1-1300 | -0,60 | -0,18 | 0,3337 | 179,35 | -7,35 | 54,05 | 2,67 | ||
| 1300,1-1500 | -0,01 | 0,00 | 0,3989 | 214,44 | 29,56 | 873,70 | 0,30 | ||
| 1500,1-1700 | 0,58 | -0,17 | 0,3365 | 180,87 | -17,87 | 319,44 | 4,07 | ||
| 1700,1-1900 | 1,17 | -0,69 | 0,2002 | 107,62 | -14,62 | 213,80 | 1,77 | ||
| 1900,1-2100 | 1,76 | -1,56 | 0,0840 | 45,17 | 18,83 | 354,42 | 1,99 | ||
| Свыше 2100,1 | 2,36 | -2,77 | 0,0249 | 13,38 | -0,38 | 0,14 | 7,85 | ||
| Итого | 0,01 | ||||||||
| 22,63 |
В связи с тем, что табличные значения рассчитаны для непрерывно изменяющегося признака с дисперсией равной 1, необходимо скорректировать полученные частности на фактическую величину интервала и среднеквадратическое отклонение.
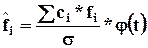 , где
, где 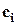 величина интервала. Так как все интервалы равны
величина интервала. Так как все интервалы равны 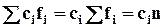 , тогда
, тогда 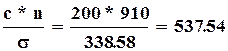 .
.
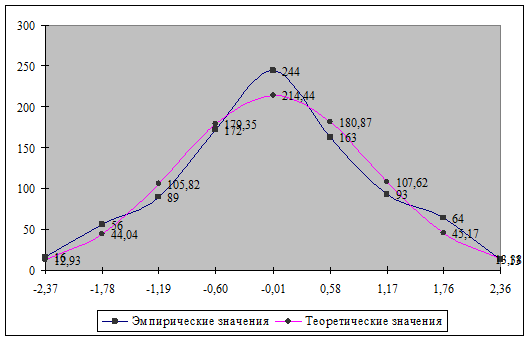
Графики не позволяют определить насколько существенны отклонения эмпирических и теоретических значений, поэтому более точным считается способ расчета критерия согласия Пирсона известного под названием, как «хи» квадрат:
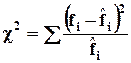 .
.
В соответствии с формулой, чем сильнее совпадение кривых, тем меньше величина 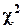 . При отсутствии отклонений
. При отсутствии отклонений 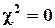 , но даже при небольших отклонениях величина
, но даже при небольших отклонениях величина 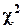 зависит от числа слагаемых, то есть от числа групп. Если
зависит от числа слагаемых, то есть от числа групп. Если 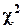 >0, то необходима его вероятностная оценка.
>0, то необходима его вероятностная оценка.
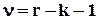 - число степеней свободы и заданная вероятность несущественности отклонений эмпирических данных и теоретических. r – число групп, k - число параметров, которые нельзя изменить.
- число степеней свободы и заданная вероятность несущественности отклонений эмпирических данных и теоретических. r – число групп, k - число параметров, которые нельзя изменить.
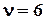
Поскольку фактическое значение 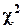 (22,63) гораздо больше табличного (5,348) даже для вероятности 0,5, гипотеза о случайном характере отклонений эмпирических данных от теоретических отклоняется.
(22,63) гораздо больше табличного (5,348) даже для вероятности 0,5, гипотеза о случайном характере отклонений эмпирических данных от теоретических отклоняется.

|
из
5.00
|
Обсуждение в статье: Тема 10.4. Сравнительная оценка параметров эмпирического и нормального распределений. Критерий Пирсона «хи» квадрат |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

