ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ

1. Доказать теорему Виета для кубического уравнения:

2. Доказать, что если уравнение с действительными коэффициентами имеет комплексный корень то и тоже является корнем этого уравнения.

3. Доказать теорему Виета для уравнения четвертой степени: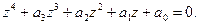

4. Доказать, что целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.

5.Доказать, что каждый многочлен нечетной степени с действительными коэффициентами имеет по крайней мере один действительный корень.

6. Используя формулу Муавра, бином Ньютона, и равенство комплексных чисел, выразить sin 4x через cos x и sin x.

7. Найти сумму биноминальных коэффициентов, т.е.

8. Вычислить:

9.Дана невырожденная матрица А. Найти определитель обратной матрицы, если известно, что

10. Доказать единственность обратной матрицы для невырожденной матрицы.

11. Доказать, что вырожденная матрица не имеет обратной.

12. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима.

13. Доказать, что система векторов, содержащая два равных вектора, линейно зависима.

14. Доказать, что система векторов, содержащая два пропорциональных вектора, линейно зависима.

15. Доказать, что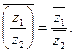

16. Доказать, что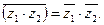

17. Доказать, что если векторы 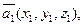линейно зависимы, то определитель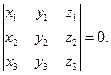

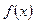18. Доказать, что если корень многочлена, , то остаток от деления многочлена на 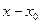равен 0.

19. Вычислить

20. Доказать, для матриц второго порядка, что

21. «Следом» 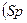квадратной матрицы называется сумма элементов главной диагонали.

Доказать, что .

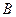22. «Следом» 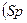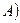квадратной матрицы называется сумма элементов главной диагонали.

Доказать, что .

23. Доказать, что если многочлен с действительными коэффициентами имеет корень то он делится (без остатка) на многочлен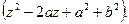

24. Используя формулу Муавра, бином Ньютона и равенство комплексных чисел выразить cos 4x через cos x и sin x.

25. Доказать, что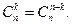

26. Доказать, что определитель диагональной матрицы равен произведению ее диагональных элементов.

27. Справедливо ли тождество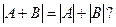

28. Числа 105, 147, 189 делятся на 21. Объясните без вычислений, почему определитель делится на 21.

29. Справедливо ли матричное тождество:

(для матриц 2-го порядка).

30. Справедливо ли матричное тождество:

(для матриц 2-го порядка).

31. Справедливо ли матричное тождество:

(для матриц 2-го порядка).

32. Доказать, что для любых трех линейно независимых векторов, 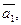векторы и - 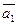линейно независимы.

33. Как изменится определитель, если все элементы в нем заменить на сопряженные?

34.Вычислить f(4), пользуясь схемой Горнера и теоремой Безу

35. Доказать, что если два многочлена f(x) и g(x), степени которых не меньше n, имеют равные значения при (n+1) значении аргументов, то эти многочлены равны.