 |
Главная |
МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ
|
из
5.00
|
3.1.1)  ; 2)
; 2)  . 3.2.1) -1; 2)
. 3.2.1) -1; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
3.3.  . 3.4.1) не существует; 2)
. 3.4.1) не существует; 2)  ; 3)
; 3) 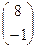 ; 4) не существует.
; 4) не существует.
3.5.1)  ; 2)
; 2) 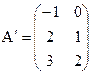 ; 3)
; 3)  ; 4)
; 4)  .
.
3.6. 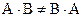 , т.к., если
, т.к., если  ,
,  ,
,  ,
,  .
.
3.7.1)  ; 2)
; 2) 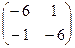 .
.
3.8.1) 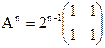 ; 2)
; 2)  ; 3)
; 3) 

 ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
3.9.1) Вид определяется неоднозначно, например:  ;
;
2)  .
.
3.10.1)  ; 2)
; 2)  .
.
ОПРЕДЕЛИТЕЛИ
3.12. 1) 1; 2) -2; 3) -1; 4) 0; 5) -3; 6) 13.
3.14.1) 40; 2) -3; 3) abc; 4) abc; 5)  ; 6) 1; 7) -i; 8) 9i+15.
; 6) 1; 7) -i; 8) 9i+15.
3.16.3) Умножим элементы 1-го столбца на 10 и прибавим по 2-му столбцу.
 на определитель,
на определитель,  исходный определитель делится на 19.
исходный определитель делится на 19.
3.17.1) 1; 2) 5; 3) 0; 4) 15; 5) -2i; 6) abcd; 7)  ; 8)
; 8)  .
.
Глава 4.
ОБРАТНАЯ МАТРИЦА. РАНГ МАТРИЦЫ. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ.
4.2.1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 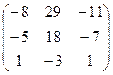 .
.
4.3.1) r = 0; 2) r = 1; 3) r = 2; 4) r = 2; 5) r = 2; 6) r = 2; 7) r = 2; 8) r = 4.
4.4.матрицы с нулевыми элементами.
4.5.матрицы со всеми пропорциональными строками или столбцами, а также матрицы, имеющие одну ненулевую строку или столбец.
4.6. 

 .
.
r = n (числу ненулевых элементов).
4.7.1) возможно, не всегда; 2) возможно, выполняется не всегда;
3) возможно, выполняется не всегда; 4) возможно, выполняется не всегда;
5) возможно, выполняется не всегда; 6) возможно, выполняется всегда.
4.8.1) (1,4,-7,7); 2) (0,0,0,0).
4.9.1) система линейно независима; 2) система линейно независима;
3) система линейно независима; 4) система линейно зависима;
5) система линейно зависима; 6) система линейно независима.
Глава 5.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
5.1.1) система совместна, х =1, у =1, z =1; 2) система совместна, x = -1, y = 0, z = 1;
3) система несовместна; 4) система несовместна; 5) система совместна, 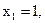


 6) система совместна,
6) система совместна, 



5.2.1) общее решение:  ,
,  ; частное решение:
; частное решение:  ;
;
ФСР:  ,
,  ;
;
2) общее решение:  ; частное решение:
; частное решение: 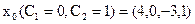 ; ФСР:
; ФСР:  ,
,  ,
,  ;
;
3) общее решение:  ; частное решение:
; частное решение:  ; ФСР: n – r = 3-1=2,
; ФСР: n – r = 3-1=2,  ,
,  :
:  ;
;  ,
,  :
:  ,
,  ;
;
4) общее решение:  ; частное решение:
; частное решение:  ; ФСР: n – r = 3,
; ФСР: n – r = 3,  ,
,  ,
,  :
:  ;
;  ,
,  ,
,  :
:  ,
,  ,
,  ,
, 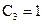 :
: 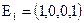 ;
;  +
+  ;
;
5) общее решение:  ; частное решение:
; частное решение:  ; ФСР: n – r = 4,
; ФСР: n – r = 4,  ,
,  ,
,  ,
, 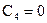 :
:  ;
;  ,
,  ,
,  ,
, 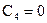 :
: 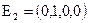 ,
,  ,
,  ,
, 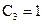 ,
, 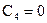 :
:  ;
;  ,
,  ,
,  ,
,  :
:  ;
;
 +
+  +
+  ;
;
6) общее решение:  ; частное решение:
; частное решение:  ; ФСР: n – r = 3-1=2,
; ФСР: n – r = 3-1=2,  ,
,  ,
,  ;
;
 ,
,  ,
,  ,
,  .
.
5.3.1) система совместная, неопределенная. Общее решение: х = (1, -С, С);
2) система совместная, неопределенная. Общее решение:  .
.
5.4.1) определена,  , r (А) = 3; 2) несовместна, а= -3,
, r (А) = 3; 2) несовместна, а= -3,  ;
;
3) неопределенна а= -3,  .
.
5.5.1) определена, при 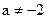 ,
,  r (А) = 3; 2) несовместна, при а= -2;
r (А) = 3; 2) несовместна, при а= -2;
3) неопределенна, при а= 1.
Глава 6.
СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ.
ЛИНЕЙНЫЕ ПРОСТРАНСТВА.
6.1. 1) 
 ,
, 
 ,
,  ;
;
2) 
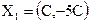 ,
, 
 ,
,  ;
;
3) 
 ; 4)
; 4) 
 ;
;
5) 
 ,
, 
 ,
, 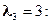
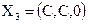 ;
;
6) 
 ,
, 
 ,
, 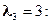
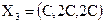 ;
;
7) 
 ,
,  комплексные;
комплексные;
8) 
 ;
; 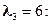
 ;
;
9) 
 ,
, 

10) 
 ,
, 
 ,
, 
 ;
;
11) 
 ,
, 
 ,
, 
 ;
;
12) 
 ,
, 
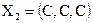 ,
, 
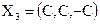 .
.
6.2. 


собственные значения равны диагональным элементам.
6.4. 
по аналогии с 6.2. 
6.5. 

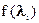 .
.
6.6.1) является; 2) не является; 3) не является; 4) является; 5) является; 6) является;
7) не является; 8) является; 9) является; 10) не является; 11) не является; 12) является;
13) является; 14) является; 15) является; 16) является; 17) не является; 18) является;
19) не является; 20) является.
Глава 7.
БАЗИС. МАТРИЦЫ ПЕРЕХОДА. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ.
7.1. 1) ненулевой вектор, лежащий на прямой;
2) любые два неколлинеарных вектора на плоскости;
3) две матрицы, например  и
и  ;
;
4) три многочлена, например 1, х,  .
.
7.2.1) базис состоит из  ; 2) базис состоит из
; 2) базис состоит из  .
.
7.3.1) Х(1/3,1/3,1/3); 2) X(0,-5,4).
7.4.1) f(t) = (5,2,-1,1); 2) f(t) = (4,2,-1,1); 3) f(t) = (5,2,-1,-5).
7.5.1)  , базис, например,
, базис, например, 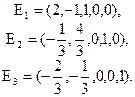
7.6.1)  ; 2)
; 2)  .
.
7.7.1) 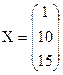 ; 2)
; 2)  .
.
7.8.1) с = (2,2,1,0), d= (-5,2,6,1); 2) с = (1,-2,1,0), d= (17/6,-2/3,-25/6,1).
7.9.1) один из векторов  ;
;
2)  ,
,  .
.
7.10.Процессом ортогонализации системы векторов 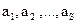 называется переход от этой системы к новой системе
называется переход от этой системы к новой системе  , построенной следующим образом:
, построенной следующим образом: 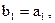
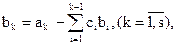 где
где  если
если  и
и  - любое число, если
- любое число, если  .
.
1)  ,
,  ,
,  ;
;
2)  ,
,  .
.
Глава 8.
МАТРИЦЫ ОПЕРАТОРОВ.
8.1.  . 8.2.1)
. 8.2.1)  ; 2)
; 2)  .
.
8.3.1)  ; 2)
; 2) 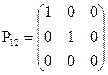 ; 3)
; 3)  ; 4)
; 4) 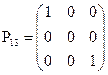 ;
;
5)  .
.
КВАДРАТИЧНЫЕ ФОРМЫ.
8.5.1)  , положительно определенная; 2)
, положительно определенная; 2)  , знакопеременная;
, знакопеременная;
3)  , положительно определенная; 4)
, положительно определенная; 4)  , знакопеременная;
, знакопеременная;
5)  , знакопеременная; 6)
, знакопеременная; 6)  , знакопеременная;
, знакопеременная;
7)  , положительно определенная; 8)
, положительно определенная; 8)  знакопеременная.
знакопеременная.
Глава 9.
|
из
5.00
|
Обсуждение в статье: МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

