 |
Главная |
УРАВНЕНИЕ ПЛОСКОСТИ. УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
|
из
5.00
|
13.1. Даны две точки  и
и  . Составить уравнение плоскости перпендикулярной прямой
. Составить уравнение плоскости перпендикулярной прямой  , проходящей через
, проходящей через  .
.
13.2. Составить уравнение плоскости, проходящей через точку  параллельно двум векторам
параллельно двум векторам  и
и  .
.
13.3.Составить уравнение плоскости, проходящей через три точки  ,
, 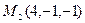 и
и  .
.
13.4.Определить взаимное расположение следующих пар плоскостей (перпендикулярны, параллельны, пересекаются): 1)  ;
;
2) 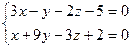 ; 3)
; 3)  ; 4)
; 4) 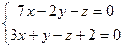 ;
;
5) 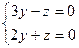 ; 6)
; 6)  .
.
13.5. Составить уравнение плоскости, которая проходит через т. 
перпендикулярно двум плоскостям 2х-z+1=0 и у=0.
13.6. Установить, что три плоскости х-2у+z-7=0, 2х+у-z+2=0, х-3у+2z-11=0,
имеют одну общую точку и найти ее.
13.7. Доказать, что три плоскости 7х+4у+7z+1=0, 2х-у-z+2=0, х+2у+3z-1=0, проходят через одну прямую.
13.8.Доказать, что три плоскости 2х-у+3z-5=0, 3х+у+2z-1=0, 4х+3у+z+2=0, пересекаются по трем различным параллельным прямым.
13.9.Найти расстояние между параллельными плоскостями: 1)  ;
;
2) 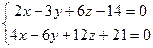 ; 3)
; 3)  .
.
13.10. Составить уравнения плоскостей, которые делят пополам двугранные углы,
образованные пересекающимися плоскостями: 1)  ;
;
2)  .
.
13.11. Составить уравнение плоскости, проходящей через прямую пересечения
плоскостей 2х-у+3z-5=0 и х+2у-z+2=0 параллельно вектору 
13.12. Составить уравнение плоскости, проходящей через прямую 
перпендикулярно плоскости х+19у-7z-11=0.
13.13. Дана прямая, составить канонические и параметрические уравнения прямой:
1) 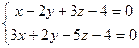 ; 2)
; 2)  ; 3)
; 3)  .
.
13.14. Определить взаимное расположение прямых (перпендикулярны, параллельны):
1)  ,
,  ;
;
2) x=2t, y=3t-2, z=-6t+1 и  ;
;
3)  и
и  .
.
13.15. Определить косинус угла между прямыми:
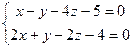 и
и  .
.
13.16. Доказать, что прямые, заданные параметрически

 и
и  , пересекаются.
, пересекаются.
13.17. Доказать, что прямая x=3t-2, y=-4t+1, z=4t-5 параллельна плоскости
4x-3y-6z-5=0.
13.18. Доказать, что прямая  лежит в плоскости 4x-3y+7z-7=0.
лежит в плоскости 4x-3y+7z-7=0.
13.19. Найти точку пересечения прямой 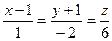 и плоскости 2x+3y+z-1=0.
и плоскости 2x+3y+z-1=0.
13.20. Найти проекцию точки Р(2,-1,3) на прямую x=3t, y=5t-7, z=2t+2.
13.21. Найти проекцию точки Р(5,2,-1) на плоскость 2x-y+3z+23=0.
13.22. Найти расстояние от точки Р(1,-1,-2) до прямой  .
.
13.23. Вычислить кратчайшее расстояние между прямыми:
1)  и
и  ;
;
2) x=2t-4, y=-t+4, z=-2t-1 и x=4t-5, y=-3t+5, z=-5t+5 .
КРИВЫЕ ВТОРОГО ПОРЯДКА

Найти каноническую систему координат и канонический вид кривой и построить ее в канонической системе координат.
14.1. а) 
б) 
в) 
г) 
д) 
14.2. а) 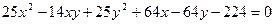
б) 
в) 
г) 
д) 
14.3. а) 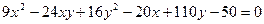
б) 
в) 
г) 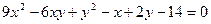
д) 
е) 

14.4. а) 
б) 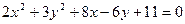
в) 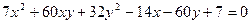
г) 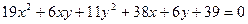
д) 
е) 
ж) 
з) 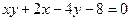
и) 
к) 
л) 
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №3
Найти каноническое уравнение кривой и построить ее
1. 
2. 
3. 
4. 
5. 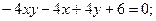
6. 
7. 
8. 
9. 
10. 
11. 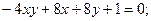
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 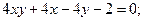
25. 
26. 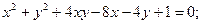
27. 
28. 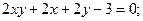
29. 
30. 
Ответы на задания по матричной алгебре.
Глава 1.
КОМПЛЕКСНЫЕ ЧИСЛА. КОМБИНАТОРИКА. БИНОМ НЬЮТОНА.
КОМПЛЕКСНЫЕ ЧИСЛА
1.1. 1) 5i+12; 2)  ; 3) 5-12i; 4) 2i-2; 5) i; 6) i+1; 7) 8-2i; 8) 23-14i; 9)
; 3) 5-12i; 4) 2i-2; 5) i; 6) i+1; 7) 8-2i; 8) 23-14i; 9) 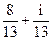 ;
;
10)  ; 11) 0,8+0,6i; 12) 0,25-0,25i.
; 11) 0,8+0,6i; 12) 0,25-0,25i.
1.2. 1)  2)
2)  3)
3)  4)
4) 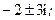 5)
5) 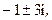 2; 6)
2; 6) 

1.3.1) 1  ; 2) 5
; 2) 5  ; 3) 2
; 3) 2 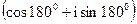 ;
;
4) 2  ; 5)
; 5)  ; 6)
; 6)  ;
;
7) 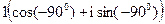 ; 8) 1
; 8) 1 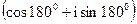 ; 9)
; 9)  ;
;
10)  ; 11)
; 11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ; 15)
; 15) 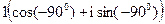 ;
;
16)  ; 17)
; 17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20) 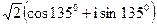 ; 21)
; 21) 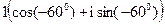 .
.
1.4.1) -1,  ; 2)
; 2) 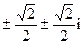 ; 3)
; 3)  ,
,  ; 4) 1,
; 4) 1,  ; 5)
; 5) 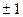 ,
,  ,
,  ;
;
6) 
 ; 7) -i,
; 7) -i,  ;
;
8)  ,
,  ; 9)
; 9) 
 ,
, 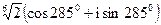 .
.
1.5.1) i; 2) 32i; 3) 64; 4) –i; 5) 4- 4i; 6) 8i; 7) 8i; 8)  ; 9) 1.
; 9) 1.
1.7.  ,
,  ,
,  ,
, 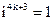 , где
, где  .
.
I; 3) -1; 4) i.
1.9.а) симметрично относительно оси ох;
б) симметрично относительно начала координат;
в) на окружности радиуса 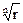 с центром в начале координат, на лучах, составляющих углы
с центром в начале координат, на лучах, составляющих углы  ,
, 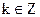 с положительным направлением оси ох.
с положительным направлением оси ох.
1.10.1)  ,
,  ; 2)
; 2) 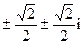 ; 3) 2,
; 3) 2,  ,
, 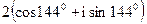 ,
,  ,
,  ; 4) i+1,
; 4) i+1,  ,
, 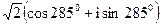 ; 5)
; 5) 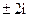 ,
,  ,
,  .
.
1.11.1) 0,  ; 2)
; 2)  ,
,  ,
,  ; 3) ki,
; 3) ki,  .
.
1.12.точка Z лежит на прямых  .
.
1.13.  . 1.14.решений нет.
. 1.14.решений нет.
КОМБИНАТОРИКА
1.15.1) 1; 2) 120; 3) 5040; 4) 56; 5) 1/7980.
1.16. 1)  , 2)
, 2)  . 1.17.7.
. 1.17.7.
1.18.1) 28; 2) 2380; 3) 6; 4) 17; 5) 101. 1.22.  .
.
БИНОМ НЬЮТОНА
1.23.1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5) - 44i+117; 6) -32i.
; 5) - 44i+117; 6) -32i.
1.24. 1) 6188  ; 2) 19448
; 2) 19448  ; 3) 136
; 3) 136  ; 4) 17
; 4) 17  .
.
1.26.1)  ; 2)
; 2)  ; 3)
; 3) 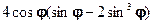 ;
;
4)  .
.
Глава 2.
МНОГОЧЛЕНЫ
2.1.1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
2.2.1)  ; 2)
; 2) 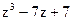 ; 3)
; 3)  ,
,  ; 4)
; 4)  .
.
2.3.1)  ; 2)
; 2)  ; 3)
; 3)  ,
,  ; 4)
; 4)  ,
,  ,
,  ; 5)
; 5)  ,
,  ,
,  ,
,  ; 6)
; 6) 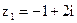 ,
,  .
.
2.5.1) z = - 2; 2) z = 2; 3) нет целых корней; 4) 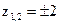 ,
,  ,
,  ; 5) z =2;
; 5) z =2;
6) нет целых корней.
2.7.1)  ; 2)
; 2) 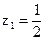 ,
,  .
.
2.10.a = -6, b= -2.
2.11.1) k=2; 2) k=3; 3) k=4; 4) k=3.
2.12.1) 
 ; 2)
; 2)  .
.
2.14.1)  , a = 4, b= -10; 2)
, a = 4, b= -10; 2)  , a = -8, b= 2.
, a = -8, b= 2.
2.15.1)  ; 2)
; 2)  .
.
2.16. 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 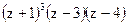 .
.
2.17.1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 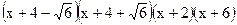 .
.
Глава 3.
|
из
5.00
|
Обсуждение в статье: УРАВНЕНИЕ ПЛОСКОСТИ. УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

