Алгебраический критерий устойчивости

Исследуем исходную СУ на устойчивость по алгебраическому критерию Гурвица. Определим передаточную функцию замкнутой системы. Обозначим вход и выход анализируемой фрагмента схемы через Y1 и Y2 соответственно, используя для этого блок В память, расположенном на вкладке Субструктуры. Два таких блока следует вынести на окно модели и присоединить к входу и к выходу СУ (рисунок 4.5).

Рисунок 4.5 - Структурная схема СУ для проведения анализа в частотной области

Выполним щелчок «мышью» по кнопке Старт (структурная схема разомкнутой СУ инициализировалась) и затем по кнопке Стоп (моделирование прервано, так и не начавшись).

В главном меню МВТУ Анализ выбрать Передаточные функции. Появляется окно Расчет передаточных функций, в котором следует записать соответствующие входы и выходы СУ. Щелкнуть по кнопке Расчет в окне Расчет передаточных функцийи через короткое время появится окно Результаты расчета передаточной функции(рисунок 4.6).

Рисунок 4.6 – Передаточная функция замкнутой СУ

Соответственно ПФ замкнутой СУ имеет вид:

,

а характеристическое уравнение СУ:

.

Составим и рассчитаем главный определитель Гурвица и его диагональные миноры для характеристического уравнения второго порядка:

, .

Δ₂ = 0.02282, Δ₁ = 0.02282.

Поскольку коэффициент а₀ > 0, то для устойчивости СУ главный определитель Гурвица и его диагональные миноры должны быть положительны. Очевидно, это условие выполняется, следовательно, исследуемая СУ устойчива.

Частотные критерии

Критерий Михайлова

Примечание.Методика исследования СУ в частотной области в данном примере выполняется в соответствии с методическими рекомендациями к лабораторной работе №3.

Исследуем исходную СУ на устойчивость по частотному критерию Михайлова. Для этого построим годограф Михайлова для замкнутой СУ (рисунок 4.7).

Рисунок 4.7 – Годограф Михайлова замкнутой СУ

Очевидно, что характеристический вектор системы начинает движение на положительной части действительной оси и поворачивается на 2 квадранта, что соответствует порядку характеристического уравнения системы. В соответствии с критерием СУ - устойчива.

Критерий Найквиста

Исследуем СУ на устойчивость по частотному критерию Найквиста. Для этого построим годограф Найквиста (рисунок 4.8) для разомкнутой СУ (2-ой весовой коэффициент в Главном сравнивающем устройстве должен быть равен нулю).

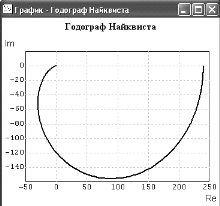Рисунок 4.8 – Годограф Найквиста разомкнутой СУ

Рассмотрим более внимательно поведение линии годографа в окрестности точки (–1; 0j) (рисунок 4.9).

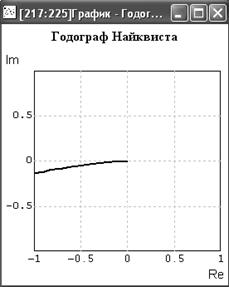Рисунок 4.9 – Годограф в окрестности точки (–1; 0j)

Очевидно, годограф не охватывает точку (–1; 0j), поэтому СУ в замкнутом состоянии будет устойчивой.