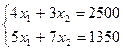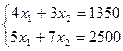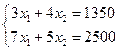|
Главная |
Функции нескольких переменных (теория, задачи)
|
из
5.00
|
1. Какова формула частного приращения функции  по аргументу
по аргументу  ?
?
а)  б)
б) 
в)  г)
г) 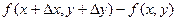
2. Закончите определение. Число  называется пределом функции
называется пределом функции  при
при  и
и  , если для любого сколь угодно малого
, если для любого сколь угодно малого 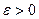 , найдется положительное число
, найдется положительное число  , такое, что для всех
, такое, что для всех  ,
,  , выполняется …
, выполняется …
а)  б)
б)  в)
в) 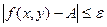 г)
г) 
3. Закончите определение. Точка  называется точкой максимума функции
называется точкой максимума функции  , если существует окрестность точки
, если существует окрестность точки  такая, что для всех точек
такая, что для всех точек  из этой окрестности выполняется …
из этой окрестности выполняется …
а)  б)
б) 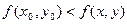
в) 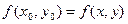 г)
г) 
4. Найти  , если
, если 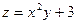
а) 2ху б) 2х в) х г) 2х+у.
5. Найти  , если
, если 
а)  б)
б)  в)
в) 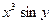 г)
г)  .
.
6. Найти  , если
, если 
а)  б)
б)  в)
в)  г)
г) 
7. Найти  , если
, если 
а)  б)
б)  в)
в)  г)
г)  .
.
8. Найти  , если
, если 
а)  б)
б)  в)
в)  г)
г)  .
.
9. Найти  , если
, если 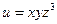
а)  б)
б) 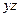 в)
в) 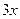 г)
г) 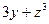 .
.
10. Найти  , если
, если 
а)  б)
б)  в)
в)  г)
г)  .
.
Кейс-задания
1.1)Предприятие производит изделия двух видов- 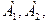 и использует для этого сырье двух типов-
и использует для этого сырье двух типов- 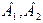 . Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:
. Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:
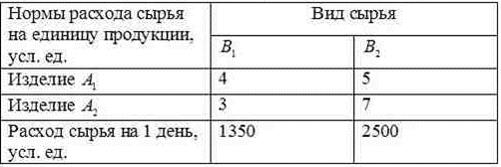
Пусть ежедневный объем выпуска изделий 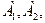 составляет
составляет 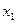 и
и  соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида изделий может иметь вид …
соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида изделий может иметь вид …
1.2) Предприятие производит изделия двух видов- 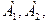 и использует для этого сырье двух типов-
и использует для этого сырье двух типов- 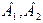 . Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:
. Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:

Установите соответствие между видом изделия и ежедневным объемом его выпуска.
1.3)Зависимость объема выпуска Y от количества используемых трудовых ресурсов L определяется функцией Y=F(L) как
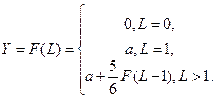
При а=8 объема выпуска не превзойдетвеличин…
Укажите не менее двух вариантов ответа:
1. 47
2. 48
3. 46
4. 49
2.1)Из половины круглого бревна с радиусом R=12 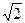 см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).
см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).

Оставшаяся часть бревна поступает в отходы.
Значение высоты балки b, при котором количество отходов минимально, равно ____см.
-
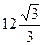
-
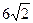
- 12
- 6
2.2) Из половины круглого бревна с радиусом R=12 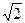 см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).
см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).

Оставшаяся часть бревна поступает в отходы.
Пусть  - площадь балки в случае, когда основание балки равно половине высоты
- площадь балки в случае, когда основание балки равно половине высоты  , а
, а 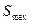 -наибольшая возможная площадь поперечного сечения балки. Тогда значение выражения
-наибольшая возможная площадь поперечного сечения балки. Тогда значение выражения 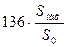 равно …
равно …
2.3) )Производительность труда рабочего в течении 8-часового рабочего дня меняется по эмпирической формулу  .
.
Средняя производительность работника (за 1 час) равна …
3.1) На рисунке изображен график скорости автомобиля V(t) при его прямолинейном движении для 0 < t <14 ,где t- время с момента старта, который состоит из отрезков прямых.

Пусть r(t)- расстояние, на которое удалился автомобиль за время t от …
Указать несколько:
- t
 (5;6)
(5;6) - t
 (11;12)
(11;12) - t
 (12;13)
(12;13) - t
 (9;10)
(9;10)
3.2) )Издержки производства С(у.е.) зависят от объема выпускаемой продукции х (ед.) как 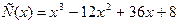 .
.
Если значения х принадлежат отрезку [2;7], то наибольшие издержки производства равны …
3.3) На рисунке изображен график скорости автомобиля V(t) при его прямолинейном движении для 0 < t <14 ,где t- время с момента старта, который состоит из отрезков прямых.

Если В-расстояние, на которое удалился автомобиль за время движения от точки старта, то значение В равно …
Вопросы к экзамену
1. Элементы теории множеств. Выпуклые множества и их свойства. Множество вещественных чисел.
2. Функция. Область определения, область значения функции. Способы задания и основные свойства функции. Основные элементарные функции, их свойства и графики.
3. Виды преобразований графиков функций. Суперпозиция функций. Обратная функция, ее график и свойства.
4. Числовые последовательности. Предел числовой последовательности. Существование предела монотонной и ограниченной последовательности.
5. Предел функции в точке и на бесконечности. Пределы монотонных функций. Свойства функций, имеющих предел в точке или на бесконечности. Замечательные пределы.
6. Бесконечно малые и бесконечно большие функции (величины), их свойства. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции, их применение в вычислениях пределов.
7. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Точки разрыва функции.
8. Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
9. Числовые ряды. Сходимость ряда. Необходимый признак сходимости ряда. Эталонные ряды.
10. Ряды с положительными членами. Признаки сравнения.
11. Ряды с положительными членами. Признаки Даламбера и Коши.
12. Ряды с членами произвольного знака. Абсолютная и условная сходимость. Признак Лейбница.
13. Степенные ряды. Область сходимости степенного ряда.
14. Ряды Маклорена и Тейлора. Разложение функций в ряды Маклорена и Тейлора.
15. Понятие функции, дифференцируемой в точке. Геометрический и физический смысл производной функции. Производная сложной и обратной функции. Правила дифференцирования, таблица производных.
16. Дифференциал функции и его геометрический смысл. Дифференцирование функций, заданных параметрически.
17. Применение дифференциала к приближенным вычислениям функций. Производные и дифференциалы высших порядков.
18. Точки экстремума функции. Теоремы Ферма, Ролля, Лагранжа, Коши, их применение.
19. Правило Лопиталя. Применение производной функции к вычислению пределов.
20. Условия монотонности функций. Экстремумы функции, необходимые и достаточные условия точек экстремума.
21. Наибольшее и наименьшее значения функции дифференцируемой на отрезке. Исследование выпуклости функции. Точки перегиба.
22. Асимптоты функции. Общая схема исследования функции и построение ее графика.
23. Первообразная. Неопределенный интеграл и его свойства. Интегрирование рациональных функций.
24. Интегрирование некоторых видов иррациональностей. Интегрирование тригонометрических функций. Таблица интегралов.
25. Методы замены и интегрирования по частям в неопределенном интеграле.
26. Определенный интеграл, его свойства. Формула Ньютона – Лейбница, ее применение в вычислении определенных интегралов. Геометрический смысл.
27. Методы замены и интегрирования по частям в определенном интеграле.
28. Двойной и тройной интегралы, их свойства.
29. Функции многих переменных. Функция двух переменных, геометрический смысл. Область определения.
30. Предел функции двух переменных. Частные производные. Полный дифференциал, его связь с частными производными.
31. Производная по направлению. Градиент.
32. Частные производные высших порядков. Экстремумы функции нескольких переменных. Необходимое условие экстремума.
33. Условный экстремум. Метод множителей Лагранжа, применение в поиске оптимальных решений.
34. Комплексные числа, действия над ними. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа.
35. Алгебраическая, тригонометрическая, показательная формы записи комплексного числа. Корни из комплексных чисел
|
из
5.00
|
Обсуждение в статье: Функции нескольких переменных (теория, задачи) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы