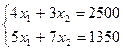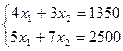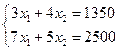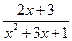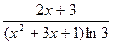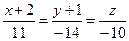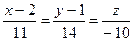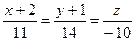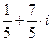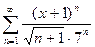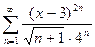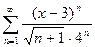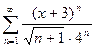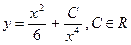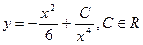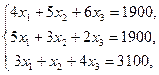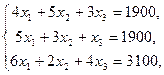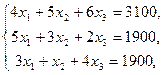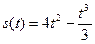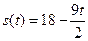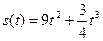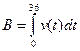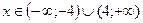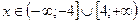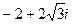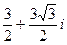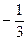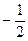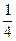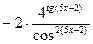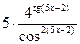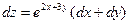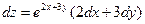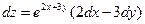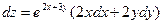|
Главная |
Регистрационный № __ от __. Контрольная работа № 1 вариант № __
|
из
5.00
|
Контрольная работа № 1 вариант № _____
Номер зачетной книжки__
Дисциплина____________
Студент (ка)____________
Факультет______________
Направление__________
Курс _________ группа ________
Оценка __________ дата ____________
Подпись преподавателя___
Проверенная контрольная работа вместе с рецензией преподавателя предъявляется
экзаменатору при сдаче зачета или экзамена
Приложение А
«Фонд оценочных средств»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
НЕФТЕКАМСКИЙ ФИЛИАЛ
Экономико-математический факультет
Кафедра математического моделирования и информационной безопасности
УТВЕРЖДЕНО
на заседании кафедры математического
моделирования и
информационной безопасности
(протокол №__ от __________)
зав.кафедрой _______________ С.И. Спивак
ФОНД
ОЦЕНОЧНЫХ СРЕДСТВ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
Математический анализ
080100-Экономика
бакалавр
Нефтекамск 2014
Контрольные работы
Пределы
8. Найти пределы функций:
а) 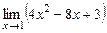 ; б)
; б) 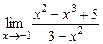 ; в)
; в)  ; г)
; г) 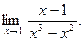
9. а)  ; б)
; б) 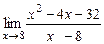 ; в)
; в) 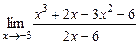 ; г)
; г) 
10. а) 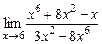 ; б)
; б) 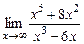 ; в)
; в)  ; г)
; г) 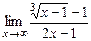 ;
;
д) 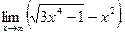
11. а) 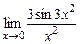 ; б)
; б) 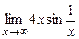 ; в)
; в)  .
.
12. а) 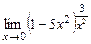 ; б)
; б) 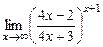 ; в)
; в) 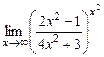 ; г)
; г) 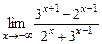 ;
;
д) 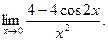
Найти пределы, используя эквивалентность бесконечно малых функций.
13. а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 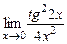 ;
;
д) 
14. а) 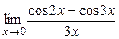 ; б)
; б) 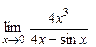 ; в)
; в)  ; г)
; г)  ;
;
д) 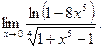
Производные
7. Найти производные функции: а) 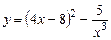 ; б)
; б)  ;
;
в) 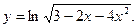
8. а) 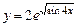 ; б)
; б) 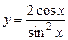 ; в)
; в) 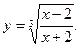
9. а) 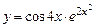 б)
б) 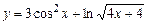 ; в)
; в)  ; г)
; г) 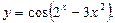
10. а)  ; б)
; б) 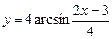 ; в)
; в) 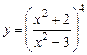 ; г)
; г) 
Найти пределы, используя правило Лопиталя:
11. а)  ; б)
; б) 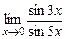 ; в)
; в)  ; г)
; г) 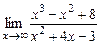 ;
;
д) 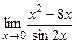 е)
е) 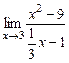 ; ж)
; ж) 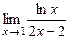 ; з)
; з) 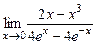 .
.
12. Исследовать функцию и построить ее график: а)  .
.
Интегралы
7. Найти интегралы:
а) 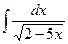 б)
б) 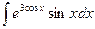 в)
в) 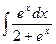
г)  д)
д) 
8. Найти интегралы, используя метод интегрирования по частям:
а) 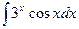 б)
б)  в)
в) 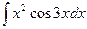
9. Найти интегралы, используя метод неопределённых коэффициентов:
а) 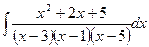 б)
б) 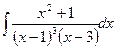 в)
в) 
10. Вычислить площадь плоской фигуры в прямоугольных координатах:  .
.
11. Вычислить площадь плоской фигуры, ограниченной кривыми:
а) 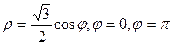 б)
б) 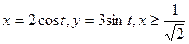 .
.
12. Найти длину дуги кривой
а) 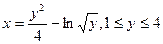 б)
б) 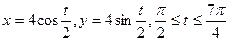
в) 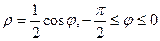
Функции нескольких переменных
9. 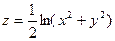 . Найти
. Найти  .
.
10. Показать, что функция 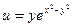 удовлетворяет уравнению
удовлетворяет уравнению  .
.
11. Найти производную функции 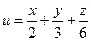 в направлении
в направлении  в произвольной точке.
в произвольной точке.
12. Найти наибольшее и наименьшее значения функции 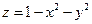 в круге
в круге 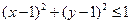 .
.
13. Найти экстремумы функции 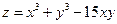 .
.
14. 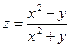 , где
, где  . Найти
. Найти 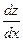 .
.
15. 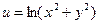 , где
, где 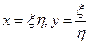 . Найти
. Найти 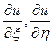 .
.
16.  , где
, где 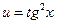 ,
, 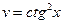 . Найти
. Найти 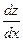 .
.
Комплексные числа
3. Даны два комплексных числа  . Требуется:
. Требуется:
е) изобразить эти комплексные числа;
ж) найти сумму, разность, произведение, частное этих комплексных чисел;
з) записать эти числа в тригонометрической и показательной формах;
и) найти  ;
;
к) найти 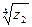 .
.
4. Решить уравнения: а) 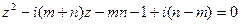 ; б)
; б)  .
.
Критерии выставления баллов за контрольную работу в соответствие с балльно-рейтинговой системой приведены в следующей таблице. Полнота и правильность решений оценивается с точки зрения применения полученных знаний и математических методов к решениям конкретных задач, на основе знаний, умений и навыков, полученных на лекционных, практических занятиях и при выполнении самостоятельной работы.
| Кол-во баллов | Критерии оценки | Формируемые компетенции |
| 10 баллов | Даны полные и правильные решения на 85-100% задач контрольной работы. Студент показывает умение правильно применять математический аппарат и знания к конкретным ключевым задачам, демонстрирует сформированность всех компетенций. | ПК-4 |
| 8-9 баллов | Даны правильные решения на 70-84% задач контрольной работы. В остальных задачах есть недочеты или несущественные ошибки. Студент показывает умение применять математический аппарат к конкретным ключевым задачам, демонстрирует наличие основной компетенции. | ПК-4 |
| баллов | Даны правильные решения на 50-69% задач контрольной работы. В остальных задачах есть недочеты или существенные ошибки. Студент показывает недостаточные умения применять математический аппарат к конкретным ключевым задачам, демонстрирует некоторое наличие компетенции ПК-1 | ПК-4 |
| 3-6 баллов | Правильно выполнены только 30-49% задач контрольной работы. Студент допускает грубые, существенные ошибки при решениях задач. | __ |
| 0-2 баллов | Решены правильно менее 30% задач контрольной работы. Либо студент присутствовал на контрольной работе, но не сдал ее преподавателю. | __ |
Итоговое тестирование
Тестовые задания разрабатываются на основе программы дисциплины, вопросов к экзамену и формируемым компетенциям. База тестовых контрольных заданий представлена в тестовой оболочке SunRav на server-domain.
Итоговый тест содержит основные темы дисциплины и кейс-задания.
Критерии оценки итогового теста:
4) от 0 до 5 баллов – «удовлетворительно» (некоторое наличие компетенции ПК-4);
5) от 5 до 7 баллов – «хорошо» (частично освоена компетенция ПК-4);
6) от 8 до 10 баллов – «отлично» (освоена компетенция ПК-4).
Для подготовки к итоговому тестированию студенты получают примерную базу тестовых заданий. Ниже приведены примерные тесты из базы тестовых заданий и кейс-задания.
Вариант 1
1. Даны матрицы 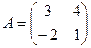 и В =
и В =  . Тогда матрица C=A*B имеет вид:
. Тогда матрица C=A*B имеет вид:
· 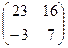
· 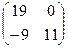
· 
· 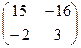
2. Дан параллелограмм OABC. Векторы 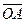 =(-2;3;1),
=(-2;3;1), 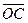 =(2;-5;3). Тогда вектор
=(2;-5;3). Тогда вектор 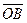 имеет координаты
имеет координаты
· (4;-8;2)
· (0;2;-4)
· (0;-2;4)
· (-4;8;-2)
3. Дано уравнение прямой 2x+3y-6=0. Тогда уравнение этой прямой «в отрезках» имеет вид
· 
· 
· 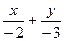 =1
=1
· 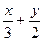 =1
=1
4. Общее уравнение плоскости, проходящей через точку А(-2,0,3) параллельно плоскости x-2y+4z-8=0 имеет вид …
· x-2y+4z+8=0
· x-2y+4z-8=0
· x-2y+4z+10=0
· x-2y+4z-10=0
5. Произведение комплексных чисел 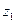 =
= 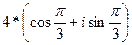 и
и  равно…
равно…
· 7
· 12
· 12i
· 7i
6. Предел 
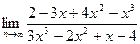 равен …
равен …
· 
· 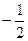
· 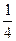
· - 
7. производная функции y= 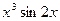 равна …
равна …
· 
· 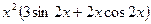
· 
· 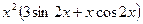
8. Полный дифференциал функции 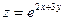 имеет вид …
имеет вид …
· 
· 
· 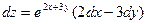
· 
9. Неопределенный интеграл 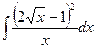 равен …
равен …
· 
· 
· 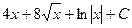
· 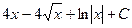
10. Определенный интеграл 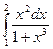 равен
равен
· 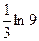
· 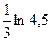
· 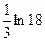
· 
11. Радиус сходимости степенного ряда 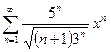 равен …
равен …
· 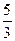
· 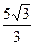
· 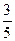
· 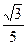
12. Уравнение 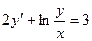 является …
является …
· Дифференциальным уравнением с разделяющимися переменными
· Линейным дифференциальным уравнением первого порядка
· Уравнение Бернулли
· Однородным относительно x и y дифференциальным уравнением первого порядка
13. Прямая 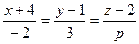 и плоскость 4x+By-2z+6=0 перпендикулярны при значениях p и B , равных …
и плоскость 4x+By-2z+6=0 перпендикулярны при значениях p и B , равных …
· p=-1 B=6
· p=-1 B=-6
· p=1 B=6
· p=1 B=-6
14. Произведение комплексных чисел 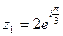 и
и 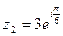 равно
равно
· 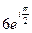
· 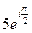
· 
· 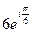
15. Модуль градиента функции нескольких переменных 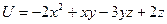 в точке М(1,-2,0) равен …
в точке М(1,-2,0) равен …
· 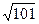
· 73
· 101
· 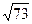
16. Множество первообразных функций f(x)=arctg3x имеет вид …
· 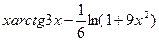 +C
+C
· 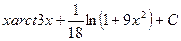
· 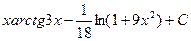
· 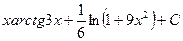
18. Вероятность появления события A в каждом из 400 проведенных испытаний равна 0,6. Тогда вероятность того, что число Х появлений события А будет заключено в пределах от 230 до 250, можно оценить с использованием неравенства Чебышева как …
- Р
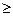 0,004
0,004 - Р=0,04
- P<0.04
- P
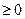
19.1)Предприятие производит изделия двух видов- 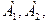 и использует для этого сырье двух типов-
и использует для этого сырье двух типов- 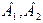 . Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:
. Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:

Пусть ежедневный объем выпуска изделий 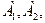 составляет
составляет 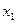 и
и  соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида изделий может иметь вид …
соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида изделий может иметь вид …
19.2) Предприятие производит изделия двух видов- 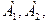 и использует для этого сырье двух типов-
и использует для этого сырье двух типов- 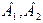 . Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:
. Нормы затраты сырья на единицу продукции каждого вида и объем расхода за 1 день заданы на таблице:

Установите соответствие между видом изделия и ежедневным объемом его выпуска.
19.3)Зависимость объема выпуска Y от количества используемых трудовых ресурсов L определяется функцией Y=F(L) как
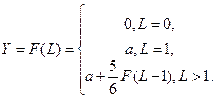
При а=8 объема выпуска не превзойдетвеличин…
Укажите не менее двух вариантов ответа:
1. 47
2. 48
3. 46
4. 49
20.1)Из половины круглого бревна с радиусом R=12 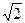 см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).
см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).

Оставшаяся часть бревна поступает в отходы.
Значение высоты балки b, при котором количество отходов минимально, равно ____см.
-
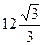
-
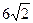
- 12
- 6
20.2) Из половины круглого бревна с радиусом R=12 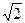 см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).
см вытесывается балка с прямоугольным поперечным сечением, основание которого равно а и высота b(см. рисунок).

Оставшаяся часть бревна поступает в отходы.
Пусть 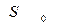 - площадь балки в случае, когда основание балки равно половине высоты
- площадь балки в случае, когда основание балки равно половине высоты  , а
, а 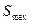 -наибольшая возможная площадь поперечного сечения балки. Тогда значение выражения
-наибольшая возможная площадь поперечного сечения балки. Тогда значение выражения 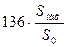 равно …
равно …
20.3) )Производительность труда рабочего в течении 8-часового рабочего дня меняется по эмпирической формулу  .
.
Средняя производительность работника (за 1 час) равна …
21.1) На рисунке изображен график скорости автомобиля V(t) при его прямолинейном движении для 0 < t <14 ,где t- время с момента стврта, который состоит из отрезков прямых.

Пусть r(t)- расстояние, на которое удалился автомобиль за время t от …
Указать несколько:
- t
 (5;6)
(5;6) - t
 (11;12)
(11;12) - t
 (12;13)
(12;13) - t
 (9;10)
(9;10)
21.2) )Издержки производства С(у.е.) зависят от объема выпускаемой продукции х (ед.) как 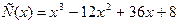 .
.
Если значения х принадлежат отрезку [2;7], то наибольшие издержки производства равны …
21.3) На рисунке изображен график скорости автомобиля V(t) при его прямолинейном движении для 0 < t <14 ,где t- время с момента старта, который состоит из отрезков прямых.

Если В-расстояние, на которое удалился автомобиль за время движения от точки старта, то значение В равно …
Вариант 2
Задание 1. Даны матрицы А= 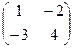 и В=
и В= 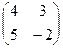 . Тогда матрица С=А*В имеет вид…
. Тогда матрица С=А*В имеет вид…
А) 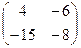
Б) 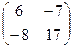
В) 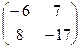
Г) 
Задание 2. дан параллелограмм ОАВС. Векторы 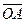 =(-2;3;1),
=(-2;3;1), 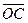 =(2;-5;3). Тогда вектор
=(2;-5;3). Тогда вектор 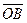 имеет координаты…
имеет координаты…
А) (-4;8;-2)
Б) (0;-2;4)
В) (4;-8;2)
Г) (0;2;-4)
Задание 3.
Общее уравнение прямой, проходящей через точку А(-3;2) параллельно прямой x-5y+11=0, имеет вид …
- x-5y-13=0
- x-5y+13=0
- 5x+y-3=0
- 5x+y+13=0
Задание 4. Плоскости 2х-5у+z+7=0 и mx+y-3z+1=0 перпендикулярны при значении m, равном…
А) 4,5
Б) -6
В) 4
Г) 2
Задание 5. Значение выражения 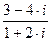 равно…
равно…
A) 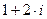
Б) 
B) 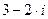
Г) 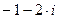
Задание 6. Предел  равен…
равен…
А) 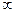
Б) 
В) 1
Г) 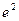
Задание 7.
Производная функции  равна …
равна …
8)Определенный интеграл  равен …
равен …
-

- 30
- 19
- 21
Задания 9. Неопределенный интеграл 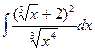 равен…
равен…
А) 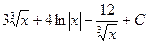
Б) 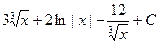
В) 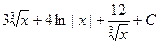
Г) 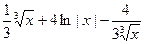
Задание 10. Определенный интеграл 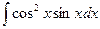 равен…
равен…
А) 0
Б) 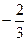
В) 2
Г)  1
1
Задание 11. Радиус сходимости степенного ряда 
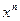 равен
равен
-
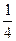
-

- 2
- 4
Задание 12.Уравнение 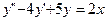 является …
является …
- дифференциальным уравнением с разделяющимися переменными
- линейным дифференциальным уравнением первого порядка
- линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
- линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
Задание 13.Конаническое уравнение прямой  может иметь вид…
может иметь вид…
Задание 14. Значение выражения  равно …
равно …
Задание 15. градиент функции нескольких переменных 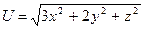 в точке пересечения оси Oz (z>0) с поверхностью U=3 равен …
в точке пересечения оси Oz (z>0) с поверхностью U=3 равен …
-
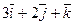
- 2

-

- 3
 +2
+2 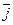 +3
+3
Задание 16.Множество первообразных функции 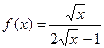 имеет вид …
имеет вид …
1. 
2. 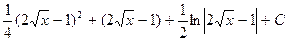
3. 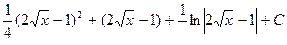
4. 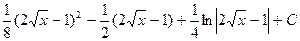
Задание 17.Интервал сходимости имеет вид 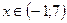 для степенного ряда …
для степенного ряда …
Задание 18.Общее решение дифференциального уравнения  имеет вид …
имеет вид …
Задание 19.1.
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок. При этом используется сырье трех типов: 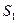 ,
, 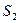 ,
, 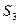 . Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:

Пусть ежедневный объем выпуска сапог, кроссовок и ботинок составляет 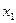 ,
,  ,
, 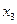 соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида обуви может иметь вид …
соответственно, тогда математическая модель для нахождения ежедневного выпуска каждого вида обуви может иметь вид …
Задание 19.2.
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок. При этом используется сырье трех типов: 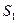 ,
, 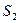 ,
, 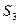 . Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:

Установите соответствие между видом изделия и ежедневным объемом его выпуска.
- Сапоги
- Кроссовки
- Ботинки
- 300
- 350
- 100
- 150
- 200
- 250
Задание 19.3
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок. При этом используется сырье трех типов: 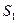 ,
, 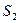 ,
, 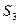 . Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:

Стоимость единицы сырья каждого типа задана матрицей-строкой В=(20 10 15). Тогда стоимость сырья, затраченного на производство сапог, составит …
20.1) Производительность труда рабочего в течении 8-часового рабочего дня меняется по эмпирической формулу  .
.
Объем выработки в течении 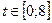 часов можно определить как …
часов можно определить как …
Задание 20.2
Для контроля уровня снега на горнолыжном склоне используются снегоуборочные машины. Изменение объема снега, выпадающего на склон в течении суток, можно описать уравнением 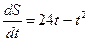 , где S(t)-объем снега (в
, где S(t)-объем снега (в 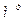 ), выпавшего на склон за время t (в часах),
), выпавшего на склон за время t (в часах),  .
.
Снегоуборочные машины работают в течении светлого времени суток с 6 до 8 часов (6< t < 18) c постоянной скоростью уборки снега 95 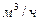 . В момент времени t=0 на склоне лежит 100
. В момент времени t=0 на склоне лежит 100 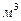 снега.
снега.
Установите соответствие между временем t и объемом снега, лежащего на склоне V(t).
- Объем снега, лежащего на склоне в момент времени t=3 часа
- Объем снега, лежащего на склоне в момент времени t=15 часов
- 820
- 199
- 800
- 520
- 200
Задание 20.3
Для контроля уровня снега на горнолыжном склоне используются снегоуборочные машины. Изменение объема снега, выпадающего на склон в течении суток, можно описать уравнением 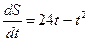 , где S(t)-объем снега (в
, где S(t)-объем снега (в 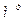 ), выпавшего на склон за время t (в часах),
), выпавшего на склон за время t (в часах),  .
.
Снегоуборочные машины работают в течении светлого времени суток с 6 до 8 часов (6< t < 18) c постоянной скоростью уборки снега 95 
В момент времени t=0 на склоне лежит 100  снега.
снега.
Пусть снегоуборочные машины не работали в обыденное время (12 < t 13)?, тогда объем снега, лежащего на склоне в конце дня (t=24 ч), равен ___ м 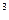 .
.
Введите ответ: ____
Задание 21. 1
На рисунке изображен график скорости автомобиля v(t) при его прямолинейном движения для 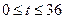 , где t-время с момента старта.
, где t-время с момента старта.

График состоит из трех полуокружностей с радиусами 9, 4,5 и -4,5 соответственно.
Пусть А-сумма всех значений t из отрезка 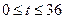 , в которых ускорение автомобиля равно нулю. Тогда значение А равно …
, в которых ускорение автомобиля равно нулю. Тогда значение А равно …
- 63
- 27
- 16,5
- 36
Задание 21.2 На рисунке изображен график скорости автомобиля v(t) при его прямолинейном движения для 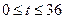 , где t-время с момента старта.
, где t-время с момента старта.

График состоит из трех полуокружностей с радиусами 9, 4,5 и -4,5 соответственно.
Пусть В-расстояние, на которое удалился автомобиль за время движения от точки старта. Тогда значение В определяется выражениями…
Выберите несколько:
Задание 21.3
На рисунке изображен график скорости автомобиля v(t) при его прямолинейном движения для 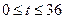 , где t-время с момента старта.
, где t-время с момента старта.

График состоит из трех полуокружностей с радиусами 9, 4,5 и -4,5 соответственно.
Если В расстояние на которое удалился автомобиль за движения от точки старта, то значение выражения 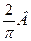 равно …
равно …
Вариант 3
1)Область определения функции  имеет вид …
имеет вид …
2) Предел 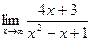 равно…
равно…
- 0
-
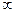
- 3
- 4
3)Для функции 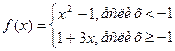
Точка х=-1 является точкой …
- устранимого разрыва
- непрерывности
- разрыва первого ряда
- разрыва второго ряда
Задание 4.Плоскости 4x-3y+2z-1=0 и 8x+ay+bz-5 параллельны при …
- a=-6, b=4
- a=-6, b=-4
- a=6, b=4
- a=6, b=-4
Задание 5 Частное от деления 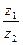 комплексных чисел
комплексных чисел  и
и 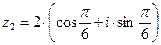 равно …
равно …
Задание 6. Предел  равен …
равен …
Задание 7. Производная функции 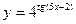 равна …
равна …
Задание 8. Полный дифференциал функции 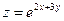 имеет вид …
имеет вид …
9)Площадь фигуры, изображенный на рисунке,
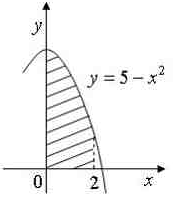
равна…
- 18
-

-
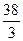
- 9
&
|
из
5.00
|
Обсуждение в статье: Регистрационный № __ от __. Контрольная работа № 1 вариант № __ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы