 |
Главная |
Дифференциальные уравнения с разделяющимися переменными
|
из
5.00
|
Это дифференциальные уравнения вида:
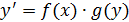
или
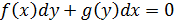
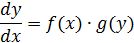

Проинтегрировав, найдем y.
Пример.
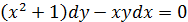
Решение:
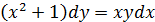
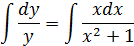

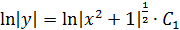

Пусть 
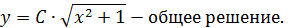
Однородные дифференциальные уравнения первого порядка.
Это дифференциальные уравнения вида:

Решается заменой
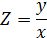

Подставим в исходное уравнение 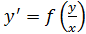 , получим
, получим
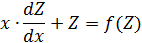


Проинтегрировав, найдем функцию Z, а затем функцию y.
Пример.
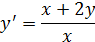
Решение:


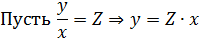

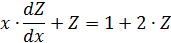
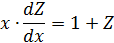
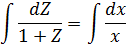
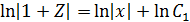
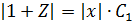
Пусть 
Тогда  , так как
, так как
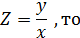

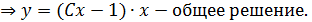
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА.
Это дифференциальные уравнения вида:

Решается подстановкой:

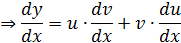
Подставим полученное в уравнение  :
:
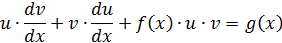
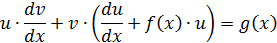
Подставив в равенство 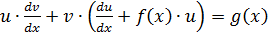 значение функции u, получим дифференциальное уравнение с разделяющимся переменными, решив которое, найдем функцию v, а затем и функцию y.
значение функции u, получим дифференциальное уравнение с разделяющимся переменными, решив которое, найдем функцию v, а затем и функцию y.
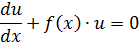
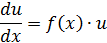
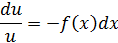
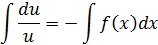
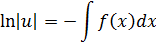
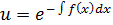
Пример.

Решение:


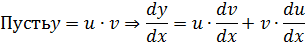
Подставим в уравнение  ,
,
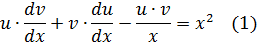


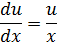
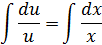
Подставим значения uв равенство (2), получим:


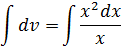

Тогда,
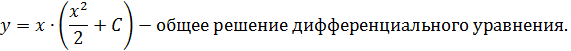
Так как при x=1, 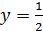 , то подставив в общее решение, получим:
, то подставив в общее решение, получим:

Подставим значение Cв общее решение, получим:
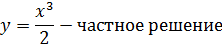
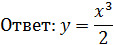
Проверка:
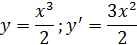




ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА.
Иногда решение дифференциальных уравнений второго порядка можно свести к последовательному решению двух дифференциальных уравнений первого порядка. Тогда говорят, что дифференциальное уравнение допускает понижение порядка.
Это дифференциальные уравнения вида:
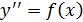
или
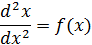
Пример 1.
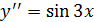

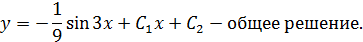
Пример 2.

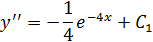
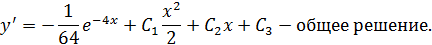
Уравнения этого типа решаются заменой переменной 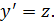 Следовательно,
Следовательно,

Подставим в дифференциальное уравнение  .
.
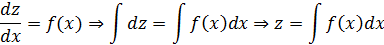
Подставив значение zв дифференциальное уравнение  , найдем функцию y.
, найдем функцию y.
Пример.

Решение:

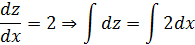



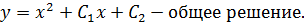
Так как при x= 1, y = 0 и при x = 1,  , то
, то
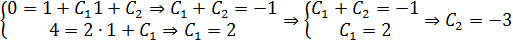

Ответ:  .
.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
Это дифференциальные уравнения вида:

При  получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
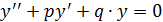
Для его решения составим характеристическое уравнение:
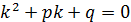
При его решении возможны следующие три случая:
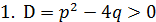

Общее решение дифференциального уравнения второго порядка находим по формуле:

2. ЕслиD=0, то общее решение находится по формуле:

Тогдаобщее решение дифференциального уравнения находим по формуле:
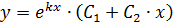
3.  , то корни комплексно - сопряженные.
, то корни комплексно - сопряженные.
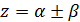
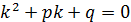

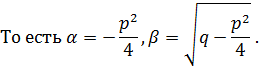
Тогда общее решение находится по формуле:
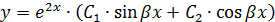
Пример 1.

Решение:

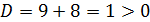
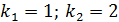
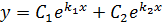

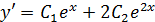
При 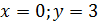
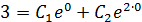
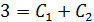
При 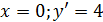
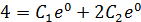


Ответ: 
Пример 2.

Решение:
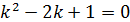
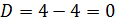
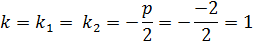
2 способ:
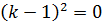
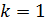


При 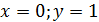

При 

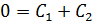

Ответ: 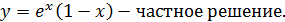
Пример 3.
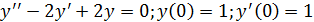
Решение:
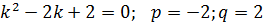
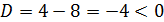

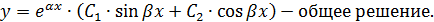
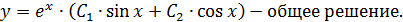

При 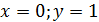
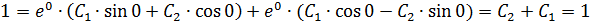
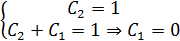
Ответ: 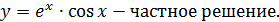
|
из
5.00
|
Обсуждение в статье: Дифференциальные уравнения с разделяющимися переменными |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

