 |
Главная |
Аппроксимация нестационарных задач
|
из
5.00
|
Рассмотрим параболическое уравнение
 L
L  в
в  (2.29)
(2.29)
с краевым условием
 на
на  (2.30)
(2.30)
и начальным условием
 в
в 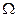 . (2.31)
. (2.31)
Аппроксимацию этой задачи проведем в два этапа.
Вначале аппроксимируем эту задачу в области  по пространственным переменным. Для этого все производные по пространственным переменным аппроксимируем разностными отношениями, затем аппроксимируем граничные условия (2.30). В итоге мы получим дифференциально-разностное уравнение и начально-краевые условия
по пространственным переменным. Для этого все производные по пространственным переменным аппроксимируем разностными отношениями, затем аппроксимируем граничные условия (2.30). В итоге мы получим дифференциально-разностное уравнение и начально-краевые условия
 L
L  в
в 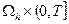 ,
,
 на
на 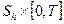 ,
,
 в
в 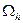 .
.
Здесь L  ,
,  сеточные операторы,
сеточные операторы,  ,
,  ,
,  ,
,  сеточные функции. Предположим, что мы можем исключить с помощью краевых условий значения
сеточные функции. Предположим, что мы можем исключить с помощью краевых условий значения  на
на  из разностного уравнения. Тогда мы приходим к следующей задаче
из разностного уравнения. Тогда мы приходим к следующей задаче
 ,
,
 ,
,
где  ,
,  ,
,  функции от
функции от 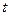 . Сеточные функции
. Сеточные функции  и
и  заданы на
заданы на 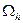 .
.
Эта задача представляет собой задачу Коши для системы обыкновенных дифференциальных уравнений относительно компонент (значений) сеточной функции  .
.
Рассмотрим эту задачу Коши
 , (2.32)
, (2.32)
 при
при  . (2.33)
. (2.33)
Предположим, что оператор  не зависит от времени. Рассмотрим простейшие аппроксимации этой задачи Коши по времени. Для удобства записи индекс
не зависит от времени. Рассмотрим простейшие аппроксимации этой задачи Коши по времени. Для удобства записи индекс  будем опускать. Зависимость сеточных функций от времени будем указывать с помощью верхнего индекса. Введем равномерную сетку узлов по времени шага
будем опускать. Зависимость сеточных функций от времени будем указывать с помощью верхнего индекса. Введем равномерную сетку узлов по времени шага  на промежутке
на промежутке  . Обозначим через
. Обозначим через  множество узлов сетки по времени. Введем обозначения
множество узлов сетки по времени. Введем обозначения
 ,
,  .
.
Наиболее простыми и употребительными аппроксимациями задачи (2.32), (2.33) являются явная и неявная схемы. Явная схема имеет вид
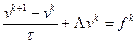 ,
, 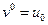 , (2.34)
, (2.34)
неявная схема
 ,
, 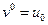 . (2.35)
. (2.35)
Явная схема потому и называется явной, что позволяет вести счет по времени по простым, рекуррентным, ''явным'' формулам.
Наряду со схемами (2.34), (2.35) большое распространение имеет схема второго порядка аппроксимации по времени – схема Кранка – Николсона
 ,
, 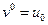 , (2.36)
, (2.36)
где
 или
или  .
.
Схемы (2.34)-(2.36) называются двухслойными. Приведем пример многослойной схемы:
 ,
, 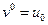 .
.
Для этих схем требует уточнения вопрос о начале счета.
Разрешая схемы (2.34)-(2.36) относительно  , получим, что для всех трех схем
, получим, что для всех трех схем  определяется из следующего рекуррентного соотношения:
определяется из следующего рекуррентного соотношения:
 ,
, 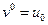 . (2.37)
. (2.37)
Оператор 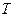 называют оператором шага, а оператор
называют оператором шага, а оператор  оператором источника. Так:
оператором источника. Так:
- для явной схемы
 ,
,  ;
;
- для неявной схемы
 ,
,  ;
;
- для схемы Кранка - Николсона
 ,
,  .
.
Представление (2.37) называется канонической формой двухслойных схем.
Уравнения вида (2.29) при условии, что L не содержит производных по времени называются эволюционными. Это название связано с тем, какого рода процессы описываются этими уравнениями.
В некоторых случаях при построении аппроксимации нестационарных задач удобно записывать разностные уравнения в виде системы двух уравнений, одно из которых аппроксимирует дифференциальное уравнение, а второе – начально-краевые условия. В этом случае разностный аналог задачи (2.29), (2.30), (2.31) примет вид
 в
в  , (2.38)
, (2.38)
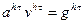 на
на  (2.39)
(2.39)
Таким образом, так же как и для стационарных задач, для начально-краевых задач строится сеточная задача, представляющая собой систему линейных алгебраических уравнений.
Так же как и для стационарных задач, вводится понятие аппроксимации исходной задачи сеточной задачей.
Говорят, что задача (2.38), (2.39) аппроксимирует исходную задачу на точном решении с порядком  по пространственным переменным и с порядком
по пространственным переменным и с порядком  по времени, если
по времени, если
 ,
,
 .
.
Как и для стационарных задач, оператор 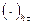 сопоставляет функции
сопоставляет функции  сеточную функцию из пространства
сеточную функцию из пространства  сеточных функций, заданных на
сеточных функций, заданных на  . Например,
. Например, 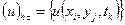 .
.
Предположив, что решение задачи (2.29)-(2.31) имеет вторые производные по времени, можно показать, что схемы (2.34), (2.35) имеют первый порядок аппроксимации по времени. В этом можно убедиться, используя разложение точного решения по формуле Тейлора. Что касается схемы (2.36), то при достаточной гладкости точного решения она имеет второй порядок аппроксимации по времени.
Пример. Рассмотрим начально-краевую задачу
 в
в  ,
,  ,
,
 на
на  ,
,
 в
в  .
.
Введем
 ,
,

В качестве аппроксимирующей примем задачу, записанную в операторной форме:
 в
в  ,
,
 на
на  ,
,
 в
в  .
.
Рассмотрим простейшую явную аппроксимацию:
 ,
,
 ,
,
 ,
,
 .
.
Тогда
 в
в  ,
,
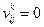 на
на  ,
,
 в
в  .
.
Каноническая форма записи этой двухслойной схемы имеет вид
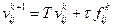 ,
,  ,
,  ,
,
где
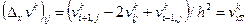 ,
,
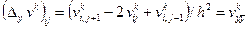 .
.
Неявная схема для рассматриваемой начально-краевой задачи имеет вид
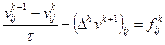 ,
,
 ,
,
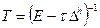 ,
,  .
.
Схема Кранка – Николсона
 ,
,
 ,
,
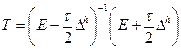 ,
,
 .
.
|
из
5.00
|
Обсуждение в статье: Аппроксимация нестационарных задач |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

