 |
Главная |
Счетная устойчивость разностных схем
|
из
5.00
|
Мы не будем стремиться к возможной общности определения понятия счетной устойчивости разностных схем, поскольку нас, в основном, будут интересовать простейшие алгоритмические подходы к анализу качества разностных схем, аппроксимирующих задачи математической физики.
Рассмотрим задачу
 в
в  , (2.40)
, (2.40)
 в
в 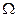 при
при  . (2.41)
. (2.41)
Пусть эта задача аппроксимируется разностной задачей
 в
в  , (2.42)
, (2.42)
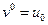 в
в 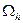 при
при  . (2.43)
. (2.43)
Будем говорить, что разностная схема (2.42), (2.43) устойчива, если при любом  , характеризующем разностную аппроксимацию, и любом
, характеризующем разностную аппроксимацию, и любом 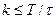 имеет место соотношение
имеет место соотношение
 ,
,
где  ,
,  постоянные, равномерно ограниченные на
постоянные, равномерно ограниченные на  и не зависящие от
и не зависящие от  ,
,  ,
,  и
и  ;
;  пространство сеточных функций, заданных на сетке, построенной там, где определена функция
пространство сеточных функций, заданных на сетке, построенной там, где определена функция  , т.е. в
, т.е. в 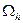 .
.
Счетная устойчивость означает непрерывную зависимость решения от входных данных для дискретных задач. Это понятие аналогично понятию корректности для стационарных задач.
В самом деле, пусть наряду с задачей (2.42), (2.43) рассматривается задача с возмущенными исходными данными  и
и  . Обозначим ее решение через
. Обозначим ее решение через  . Тогда для разности решений этих задач
. Тогда для разности решений этих задач 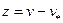 будем иметь
будем иметь
 ,
,
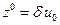 .
.
В силу устойчивости
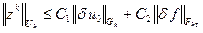 .
.
Отсюда, если возмущения  и
и  малы, то и возмущение решения
малы, то и возмущение решения  также мало.
также мало.
Введено понятие устойчивости. Возникает вопрос: какие схемы и при каких условиях устойчивы.
Решение системы (2.42), (2.43) нетрудно получить формально, запишем ее в виде
 ,
,
а затем последовательно преобразуем:

Отсюда легко получить оценку
 (2.44)
(2.44)
Здесь
 .
.
Для явной схемы отсюда с учетом того, что  , получаем
, получаем
 .
.
На самом деле здесь считается, что  , так как иначе нужно уточнять, как определяется норма оператора в оценках вида
, так как иначе нужно уточнять, как определяется норма оператора в оценках вида
 ,
,  .
.
Достаточным условием устойчивости явной схемы в силу (2.44) будет условие
 . (2.45)
. (2.45)
Критерий устойчивости будет выполнен, если
 .
.
Действительно, из (2.44) при  следует, что
следует, что
 ,
,
т.е. критерий устойчивости выполняется с постоянными  ,
,  , равномерно ограниченными на
, равномерно ограниченными на  .
.
Для неявной схемы, ввиду того что  , условие устойчивости согласно (2.44) также задается неравенством
, условие устойчивости согласно (2.44) также задается неравенством
 .
.
Следующий вопрос: когда выполняется условие  ?
?
Чтобы ответить на этот вопрос займемся установлением некоторых фактов для оценки норм.
Пусть  ,
,  , – положительно полуопределенная матрица
, – положительно полуопределенная матрица  . Тогда справедливы следующие оценки:
. Тогда справедливы следующие оценки:
1) если  , то
, то

при любых  ;
;
2) если  и
и  , то
, то
 ;
;
3) если  и
и  ,
,  , то
, то
 ;
;
4) если  и
и  , то
, то
 .
.
Доказательство утверждения 1). В силу соотношения

имеем
 .
.
Положим  , тогда
, тогда

Так как 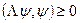 ,
,  , то при
, то при 
 .
.
Доказательство утверждения 3). Имеют место равенства
 .
.
Так как  , то
, то 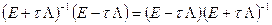 .
.
Положим  , тогда
, тогда
 .
.
Утверждения 2) и 4) очевидны.
Из этих оценок вытекает устойчивость неявной схемы и схемы Кранка – Николсона.
Таким образом, устойчивость этих схем имеет место при любом соотношении  и
и  – шагов сетки по времени и пространственным переменным.
– шагов сетки по времени и пространственным переменным.
Если устойчивость схемы имеет место при любом соотношении  и
и  , то схема называется абсолютно устойчивой.
, то схема называется абсолютно устойчивой.
Пример. В примере, где  , введем пространство
, введем пространство  как множество сеточных функций, норма в котором определяется так:
как множество сеточных функций, норма в котором определяется так:
 ,
,  ,
,  ;
;  ,
,  ,
,
а скалярное произведение соответственно
 ;
;  ,
,  .
.
Покажем, что для  справедливо утверждение
справедливо утверждение  , т.е. выполняется неравенство
, т.е. выполняется неравенство
 ,
,  .
.
Доказательство этого неравенства в нашем примере строится следующим образом. Путем суммирования по частям получаем равенство
 ,
,  .
.
Неравенство
 (2.46)
(2.46)
доказывается точно так же, как неравенство (1.61). Неравенство (2.46) – это больше, чем положительность  , это положительная определенность.
, это положительная определенность.
Таким образом, для рассмотренного нами примера неявная схема и схема Кранка – Николсона абсолютно устойчивы.
Об устойчивости явной схемы. Явная разностная схема устойчива только при определенном соотношении шагов по времени и по пространственным переменным. Рассмотрим пример
 ,
,  ,
, 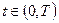 ,
,
 ,
,
 .
.
Явная схема для этой задачи будет иметь вид
 ,
, 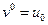 ,
,
или
 ,
, 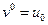 .
.
Введем в пространстве сеточных функций  сеточную норму
сеточную норму
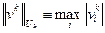 ,
,
в  и
и 
 ,
,  .
.
Тогда, в предположении, что  , т.е. при
, т.е. при  , получим неравенства
, получим неравенства
 .
.
Отсюда следует, что
 ,
,
где
 .
.
Таким образом, при  явная схема для рассматриваемой задачи является устойчивой. Следует отметить, что при
явная схема для рассматриваемой задачи является устойчивой. Следует отметить, что при  явная схема теряет устойчивость. Мы не будем останавливаться на доказательстве этого факта.
явная схема теряет устойчивость. Мы не будем останавливаться на доказательстве этого факта.
|
из
5.00
|
Обсуждение в статье: Счетная устойчивость разностных схем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

