 |
Главная |
Теоретические сведения и примеры. Пусть дано неравенство где – некоторая функция
|
из
5.00
|
Пусть дано неравенство 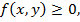 где
где  – некоторая функция. Пара чисел
– некоторая функция. Пара чисел 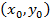 называется решением неравенства, если при подстановке в неравенство вместо х и у соответственно x0 и y0 получается верное числовое неравенство. Решить неравенство – означает найти все решения этого неравенства.
называется решением неравенства, если при подстановке в неравенство вместо х и у соответственно x0 и y0 получается верное числовое неравенство. Решить неравенство – означает найти все решения этого неравенства.
Если на плоскости задана прямоугольная декартова система координат, то совокупность точек 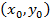 , представляющих решения неравенства, образует некоторую область. Изображение на плоскости данной области называется графическим решением неравенства.
, представляющих решения неравенства, образует некоторую область. Изображение на плоскости данной области называется графическим решением неравенства.
Для построения области решения неравенства 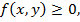 (или
(или  ) следует:
) следует:
1)построить границу области – график функции 
2) определить точки, удовлетворяющие неравенству, для чего выбрать любую точку плоскости, не принадлежащую границе, и подставить ее координаты в исходное неравенство. Если получено верное числовое неравенство, то все точки плоскости, лежащие с этой же стороны границы, являются решениями неравенства. В противном случае решениями будут точки по другую сторону границы;
3) заштриховать область решения неравенства;
4) изобразить границу пунктирной линией, если неравенство строгое  , если же неравенство нестрогое
, если же неравенство нестрогое  – сплошной, поскольку в этом случае точки, принадлежащие границе области, также являются решениями неравенства.
– сплошной, поскольку в этом случае точки, принадлежащие границе области, также являются решениями неравенства.
Замечание. Говоря о графике функции  , мы имеем в виду множество точек плоскости, удовлетворяющих данному равенству, что не является функцией в обычном школьном понимании.
, мы имеем в виду множество точек плоскости, удовлетворяющих данному равенству, что не является функцией в обычном школьном понимании.
Пример 1. Построить область решения неравенства

Решение. Строим границу области – график функции  Графиком данной функции является прямая, проходящая через точки (0; 0) и (1; –2).Выберем на плоскости произвольную точку, не принадлежащую прямой
Графиком данной функции является прямая, проходящая через точки (0; 0) и (1; –2).Выберем на плоскости произвольную точку, не принадлежащую прямой 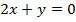 , например точку (1; 1).
, например точку (1; 1).
Поставим координаты этой точки в исходное неравенство 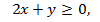 получим
получим  или
или 
или – верное числовое неравенство. Это означает, что областью решения неравенства являются все точки, расположенные по ту же сторону границы. Заштрихуем область.
Поскольку неравенство нестрогое, то границу изображаем сплошной линией (рис. 8.1).

Рис. 8.1.Область решения неравенства.
Если дана система неравенств: 
то областью её решения на плоскости ХОУ будут точки, координаты которых являются одновременно решением каждого из этих неравенств. Для построения области решения системы неравенств строят области решения каждого из неравенств и штрихуют область, общую для всех неравенств. Если такая область отсутствует, то система не имеет решения.
Пример 2. Построить на плоскости ХОУ область решения системы неравенств 
Решение. Рассмотрим каждое из неравенств в отдельности и построим их области решений.
Границей неравенства  является парабола
является парабола  с вершиной в точке (0;0) и осью симметрии ОХ, ветви направлены в сторону возрастания переменной Х. Для случайно выбранной точки плоскости (1;0), не принадлежащей границе области, неравенство
с вершиной в точке (0;0) и осью симметрии ОХ, ветви направлены в сторону возрастания переменной Х. Для случайно выбранной точки плоскости (1;0), не принадлежащей границе области, неравенство  выполняется (
выполняется (  – верное числовое неравенство). Следовательно, решением неравенства будут все точки, лежащие «внутри» параболы (рис. 8.2).
– верное числовое неравенство). Следовательно, решением неравенства будут все точки, лежащие «внутри» параболы (рис. 8.2).
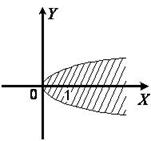
Рис. 8.2. Графическое решение неравенства.
Граница неравенства 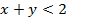 – прямая
– прямая  проходящая через точки (0; 2) и (2; 0).
проходящая через точки (0; 2) и (2; 0).
Произвольно выбранная точка (0; 0) удовлетворяет неравенству ( 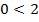 – верное числовое неравенство), поэтому областью решения неравенства будут точки плоскости, лежащие «ниже» прямой
– верное числовое неравенство), поэтому областью решения неравенства будут точки плоскости, лежащие «ниже» прямой  .
.
Неравенство строгое, поэтому границу изображаем пунктирной линией (рис. 8.3). Совместив эти два рисунка, получим область решения системы неравенств (рис. 8.4).

Рис.8.3.Решение неравенства. Рис.8.4.Решение системы неравенств.
Если неравенства, входящие в систему, содержат знак абсолютной величины, то для построения области надо раскрыть знак модуля и построить области решений, полученных при этом неравенств. По определению абсолютной величины: 
Если 
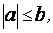 где
где 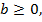 то
то  если
если 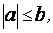 где
где 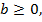 то решений нет.
то решений нет.
Если 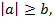 где
где  то
то  или
или  ; если
; если 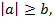 где
где  то неравенство выполняется для любых значений а.
то неравенство выполняется для любых значений а.
В ряде случаев, исходя из определения абсолютной величины, удобно не раскрывать модуль, а построить первоначально график функции, не содержащий знака модуля, а затем выполнить симметричные отображения.
Построение графика функции  Строим график функции
Строим график функции  , оставляем часть графика, лежащую выше оси ОХ, а часть графика, расположенную ниже оси ОХ, симметрично отображаем относительно оси абсцисс.
, оставляем часть графика, лежащую выше оси ОХ, а часть графика, расположенную ниже оси ОХ, симметрично отображаем относительно оси абсцисс.
Аналогично выполняется построение графика 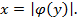
Пример 3. Построить график функции:
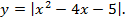
Решение. Графиком функции  является парабола c вершиной в точке (2; –9), осью симметрии, параллельной оси ОУ, ветви параболы направлены вверх. Точка пересечения с осью ОУ (0; –5); точки пересечения с осью ОХ (5; 0) и (–1; 0). Часть графика, расположенная ниже оси ОХ, симметрично отображается относительно оси абсцисс.
является парабола c вершиной в точке (2; –9), осью симметрии, параллельной оси ОУ, ветви параболы направлены вверх. Точка пересечения с осью ОУ (0; –5); точки пересечения с осью ОХ (5; 0) и (–1; 0). Часть графика, расположенная ниже оси ОХ, симметрично отображается относительно оси абсцисс.
На рис. 8.5 график функции  изображен сплошной линией.
изображен сплошной линией.
| |

Рис. 8.5. График функции 
Построение графика функции  Строим график функции
Строим график функции  Оставляем часть графика, соответствующую значениям
Оставляем часть графика, соответствующую значениям 
Симметрично отображаем эту часть относительно оси ОУ.
Пример 4. Построить график функции 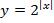 .
.
Решение. Строим график показательной функции у = 2х, оставляем часть графика, соответствующую неотрицательным значениям х, и симметрично отображаем ее относительно оси ОУ. На рис. 8.6 график изображен сплошной линией.

Рис. 8.6.График функции  .
.
Построение графика функции  .
.
Строим график функции 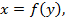 оставляем часть графика, соответствующую значениям
оставляем часть графика, соответствующую значениям  и симметрично отображаем ее относительно оси ОХ.
и симметрично отображаем ее относительно оси ОХ.
Пример 5. Построить график функции:

Решение. Строим график параболы  описанный в примере 3. Оставляем часть графика, соответствующую неотрицательным значениям у, и симметрично отображаем ее относительно оси ОХ.
описанный в примере 3. Оставляем часть графика, соответствующую неотрицательным значениям у, и симметрично отображаем ее относительно оси ОХ.
График функции  изображен на рис. 8.7 сплошной линией.
изображен на рис. 8.7 сплошной линией.

Рис. 8.7. График функции  .
.
Построение графика функции  Для построения этого графика последовательно строят графики функций
Для построения этого графика последовательно строят графики функций 
 и
и 
Пример 6. Построить график функции 
Решение. Графиком функции 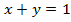 является прямая, проходящая через точки (0; 1) и (1; 0). Чтобы построить график функции
является прямая, проходящая через точки (0; 1) и (1; 0). Чтобы построить график функции 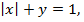 оставим часть прямой, соответствующую значениям
оставим часть прямой, соответствующую значениям  и отобразим ее симметрично оси ОУ. Затем, для полученного графика, оставим часть, соответствующую значениям
и отобразим ее симметрично оси ОУ. Затем, для полученного графика, оставим часть, соответствующую значениям  и отобразим ее относительно оси ОХ. Таким
и отобразим ее относительно оси ОХ. Таким
образом будет построен график функции  На рис. 8.8 график функции (квадрат) изображен сплошной линией.
На рис. 8.8 график функции (квадрат) изображен сплошной линией.

Рис. 8.8. График функции 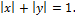
Замечание. Всякое уравнение вида  где
где  определяет квадрат с центром в начале координат и вершинами в точках (а; 0), (–а; 0), (0; а) и (0; –а). Уравнение вида
определяет квадрат с центром в начале координат и вершинами в точках (а; 0), (–а; 0), (0; а) и (0; –а). Уравнение вида  определяет смещенный относительно начала координат квадрат с центром в точке
определяет смещенный относительно начала координат квадрат с центром в точке 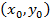 и вершинами в точках:
и вершинами в точках:  и
и 
Например, графиком функции  является квадрат с центром в точке
является квадрат с центром в точке  и вершинами в точках
и вершинами в точках  и
и 
Пример 7. Построить на плоскости ХОУ область решений системы неравенств: 
Решение. Рассмотрим неравенство  . По определению модуля неравенства
. По определению модуля неравенства 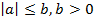 равносильны двойному неравенству
равносильны двойному неравенству  Таким образом, исходное неравенство равносильно неравенству
Таким образом, исходное неравенство равносильно неравенству  Границей области решений являются прямые
Границей области решений являются прямые  а областью решений – точки, лежащие между этими прямыми и принадлежащие прямым (рис. 8.9).
а областью решений – точки, лежащие между этими прямыми и принадлежащие прямым (рис. 8.9).
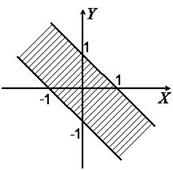
Рис. 8.9.Решение неравенства  .
.
Рассмотрим неравенство  и построим график функции
и построим график функции 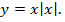
По определению модуля 
Построим параболу  для
для  и параболу
и параболу
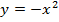 для
для  , тем самым получим график функции
, тем самым получим график функции  Поскольку
Поскольку  то областью решения неравенства являются точки, расположенные ниже графика функции (рис. 8.10).
то областью решения неравенства являются точки, расположенные ниже графика функции (рис. 8.10).

Рис. 8.10.Решение неравенства  .
.
Неравенству 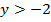 удовлетворяют точки, лежащие выше прямой
удовлетворяют точки, лежащие выше прямой  . Точки прямой не входят в область решения неравенства. Окончательно получаем область решения системы неравенств (рис. 8.11).
. Точки прямой не входят в область решения неравенства. Окончательно получаем область решения системы неравенств (рис. 8.11).
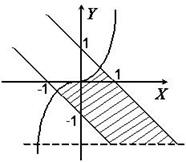
Рис. 8.11.Решение системы неравенств.
Пример 8. Построить на плоскости ХОУ область решений системы неравенств: 
Решение.
1. Рассмотрим неравенство  . Построим график функции
. Построим график функции  .
.
Если  т. е.
т. е. 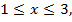
то  или
или  . Графиком функции является парабола с вершиной в точке (3; 6), ветви параболы направлены вниз. Возьмем дополнительные точки из данного интервала, например, (1; 2) и (2; 5).
. Графиком функции является парабола с вершиной в точке (3; 6), ветви параболы направлены вниз. Возьмем дополнительные точки из данного интервала, например, (1; 2) и (2; 5).
Если 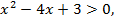 т. е.
т. е.  или
или 
то  . Это парабола с вершиной в точке (1; 2). Дополнительные точки (0; 3), (3; 6), (–1; 6), (4; 11).
. Это парабола с вершиной в точке (1; 2). Дополнительные точки (0; 3), (3; 6), (–1; 6), (4; 11).
Неравенству  удовлетворяют координаты точек, расположенных ниже графика (рис. 8.12).
удовлетворяют координаты точек, расположенных ниже графика (рис. 8.12).

Рис. 8.12.Решение неравенства  .
.
2. Рассмотрим неравенство  . Границей области является график функции
. Границей области является график функции  . Найдем область определения функции (ООФ):
. Найдем область определения функции (ООФ): 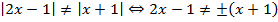 или
или  и
и 
Если  то
то  ⇒
⇒ 
Если  то
то  .
.
Если  то
то 
Построим прямые  и
и  при соответствующих значениях x с учетом ООФ. Множество точек лежит выше графика функции (рис. 8.13).
при соответствующих значениях x с учетом ООФ. Множество точек лежит выше графика функции (рис. 8.13).
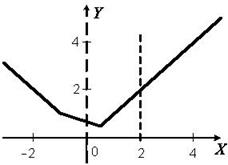
Рис. 8.13. Область определения функции.
3. Построим график функции  .
.
Данная функция четная относительно переменных x и y, поэтому ее график симметричен относительно осей координат, следовательно, достаточно построить график при  и отобразить относительно осей координат.
и отобразить относительно осей координат.
Графиком функции 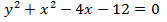 является окружность. Запишем ее каноническое уравнение:
является окружность. Запишем ее каноническое уравнение: 
 Центр окружности находится в точке (2; 0), радиус равен 4. Затем выполним симметричные отображения. Множество точек, удовлетворяющих неравенству
Центр окружности находится в точке (2; 0), радиус равен 4. Затем выполним симметричные отображения. Множество точек, удовлетворяющих неравенству  находится внутри фигуры (рис. 8.14).
находится внутри фигуры (рис. 8.14).

Рис. 8.14.Решение неравенства  .
.
Наложив три графика друг на друга, получим искомую область решения системы неравенств (рис. 8.15).

Рис. 8.15.Искомая область решения.
При решении неравенств с двумя неизвестными можно применять метод интервалов. Роль критических точек здесь играют критические линии, а роль промежутков – области. Эти линии делят ООФ двух переменных на области, где функция сохраняет знак. Для нахождения этого знака достаточно взять в рассматриваемой области какую-либо отдельную точку и найти знак функции в выбранной точке, который сохраняется во всей области.
Пример 9.Найти на плоскости ХОУ множество точек, удовлетворяющих неравенству:  .
.
Решение. ООФ:  Построим линии, определяемые равенствами
Построим линии, определяемые равенствами  и
и  .
.
В точке (2; 0) левая часть равенства равна 1, т. е. положительна. Следовательно, в области, содержащей эту точку, функция имеет знак плюс, а в остальных областях ее знаки чередуются. Решением является выделенная область на рис. 8.16.

Рис. 8.16. Географическое решение неравенства  .
.
Обычно эти задачи школьники пропускают, так как решение подобных примеров требует пространных рассуждений. Однако если попытаться решить эти задачи графически, то результаты в некоторых случаях могут быть получены значительно быстрее.
Пример 10 . Найти все значения параметра а,при каждом из которых множество решений неравенства  содержит какой-нибудь отрезок длины 2, но не содержит никакого отрезка длиной 3.
содержит какой-нибудь отрезок длины 2, но не содержит никакого отрезка длиной 3.
Решение. Поскольку неравенство содержит две переменные х и а, то его решение можно построить на плоскости в декартовой системе координат хоа (горизонтальная ось ох, вертикальная ось оа). Сразу можно отметить, что поскольку переменная х из неравенства находится в знаменателе, то 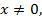 т. е. точки оси оа не являются решениями неравенства. Преобразуем неравенство к более удобному виду:
т. е. точки оси оа не являются решениями неравенства. Преобразуем неравенство к более удобному виду:





или 
Поскольку  для всех действительных х и а, кроме х = а, то достаточно потребовать, чтобы
для всех действительных х и а, кроме х = а, то достаточно потребовать, чтобы  Дробь положительна, если ее числитель и знаменатель одного и того же знака.
Дробь положительна, если ее числитель и знаменатель одного и того же знака.
Таким образом, полученное после преобразований неравенство равносильно двум системам неравенств:
 или
или 
Вторая система не имеет решений, поскольку неравенства  и
и  не могут выполняться одновременно. Для построения области решения первой системы неравенств изобразим на плоскости хоа прямые
не могут выполняться одновременно. Для построения области решения первой системы неравенств изобразим на плоскости хоа прямые  (ось оа), х = 4. Все прямые (за исключением оси) изображаются пунктиром, поскольку неравенства, входящие в систему, строгие.
(ось оа), х = 4. Все прямые (за исключением оси) изображаются пунктиром, поскольку неравенства, входящие в систему, строгие.
Областью решения исходного неравенства будет полоса  с вырезанной прямой а = х (рис. 8.17).
с вырезанной прямой а = х (рис. 8.17).

Рис. 8.17.Область решения неравенства
Для  и
и  множество решений исходного неравенства относительно переменной х содержит отрезки длиной 3, поэтому требование задачи выполняется на промежутке от 1 до 3, причем значение параметра а = 2 исключается, так как при а = 2 решение неравенства представляет собой два интервала длиной 2,
множество решений исходного неравенства относительно переменной х содержит отрезки длиной 3, поэтому требование задачи выполняется на промежутке от 1 до 3, причем значение параметра а = 2 исключается, так как при а = 2 решение неравенства представляет собой два интервала длиной 2,
но ни одного отрезка этой длины. Окончательно сделаем вывод, что при  выполняются требования задачи.
выполняются требования задачи.
Пример 11 (задание С4, варианты 31–60, 2004 г.). Найти все значения параметра а, при каждом из которых множество решений неравенства 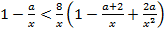 содержит какой-нибудь отрезок длиной 4 и при этом сам содержится в каком-нибудь отрезке длиной 7.
содержит какой-нибудь отрезок длиной 4 и при этом сам содержится в каком-нибудь отрезке длиной 7.
Решение. Преобразуем исходное неравенство:
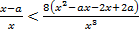




 или
или  .
.
Поскольку  для всех действительных х, кроме х = 4, а дробь положительна, если ее числитель и знаменатель одного знака, то неравенство равносильно двум системам неравенств:
для всех действительных х, кроме х = 4, а дробь положительна, если ее числитель и знаменатель одного знака, то неравенство равносильно двум системам неравенств: 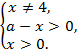 или
или 
Границами решений этих неравенств на плоскости хоа являются прямые  (ось оа).
(ось оа).
Поскольку неравенства строгие, то точки, принадлежащие указанным прямым, не являются решениями, поэтому прямые (за исключением оси оа) изображаются пунктиром. Подстановка координат произвольных точек позволяет заштриховать нужную часть плоскости, соответствующую множеству решений (рис. 8.18).
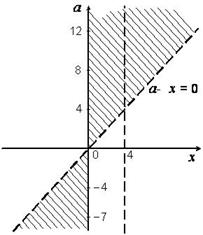
Рис. 8.18.Множество решений неравенств  .
.
Теперь, используя полученный рисунок, выберем те значения параметра а, при которых множество значений х включает в себя отрезок длиной не менее 4 и не более 7. Это условие выполнятся для 
|
из
5.00
|
Обсуждение в статье: Теоретические сведения и примеры. Пусть дано неравенство где – некоторая функция |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

