Теоретические сведения. Решение геометрических задач требует четкости в рассуждении

Решение геометрических задач требует четкости в рассуждении, понимания логических связей между различными вопросами, знания большого набора определений и теорем. Каждая геометрическая задача содержит в своем решении доказательство тех или иных фактов и вычисление некоторых элементов. Стереометрические задачи требуют также пространственного воображения, умения представлять себе рассматриваемые тела в пространстве. При использовании тех или иных утверждений должны быть указаны ссылки на соответствующие теоремы или определения. Чертеж в геометрической задаче – необходимый, но не основной компонент решения, поскольку является лишь иллюстрацией к рассуждениям. Нельзя, ссылаясь на рисунок, утверждать что-либо, хотя удачно выполненный чертеж может «подсказать» ход решения. Чертеж должен полностью соответствовать условию задачи. Текст решения должен включать в себя обозначения, указанные на чертеже.

Приведем описание некоторых геометрических фигур, вычислительные формулы и утверждения, используемые при решении геометрических задач.

Треугольник.Пусть а, b, c – длины сторон ∆ АВС, лежащие против углов А, В, С соответственно; – полупериметр; R и r – радиусы описанной и вписанной окружностей; h_a – высота, опущенная из вершины А на сторону а. Справедливы следующие утверждения:

1) площадь треугольника S может быть найдена по формулам:

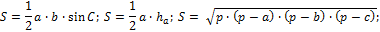
2) теорема синусов выражается формулой

3) теорема косинусов выражается формулой

4) три медианы треугольника пересекаются в одной точке, лежащей внутри треугольника (центр тяжести). Точка пересечения делит медианы на отрезки, длины которых относятся как 2 : 1 (считая от вершины);

5) три биссектрисы треугольника пересекаются в одной точке, лежащей внутри треугольника (центр вписанной окружности). Биссектриса при пересечении делит сторону на отрезки, пропорциональные прилежащим сторонам треугольника;

6) три высоты треугольника пересекаются в одной точке (ортоцентр);

7) три перпендикуляра, восстановленные к серединам сторон треугольника (срединные перпендикуляры), пересекаются в одной точке (центр описанной окружности);

8) сумма внутренних углов треугольника составляет 180^о;

9) внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним;

10) если угол С – прямой, то (теорема Пифагора).

Параллелограмм.Пусть а, b – длины смежных сторон параллелограмма ABCD; 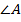– угол между этими сторонами; – высота, опущенная на сторону a; – длины диагоналей; S – площадь параллелограмма. Справедливы следующие утверждения:

1) площадь параллелограмма S может быть найдена по формулам: где – угол между диагоналями;

2) диагонали параллелограмма делятся в точке пересечения пополам;

3) параллелограмм можно вписать в окружность только тогда, когда он является прямоугольником (квадратом);

4) в параллелограмм можно вписать окружность только тогда, когда он является ромбом (квадратом).

Трапеция.Пусть a, b – длины оснований трапеции; c и d – длины боковых сторон; h – высота; S – площадь трапеции. Справедливы следующие утверждения:

1) площадь трапеции S может быть найдена по формулам:

где d₁ и d ₂ – диагонали трапеции; – угол между ними;

2) трапецию можно вписать в окружность только тогда, когда она равнобочная, т. е. c = d;

3) в трапецию можно вписать окружность только тогда, когда

Замечания. 1. Последнее утверждение справедливо для любого четырехугольника. 2. Вычисление площади по формуле имеет место для любого плоского выпуклого четырехугольника.

Окружность (круг).Пусть R – длина радиуса некоторого круга; S – его площадь; l – длина окружности, составляющая границу данного круга. Справедливы следующие утверждения:

1) площадь круга

2) длина окружности

3) площадь сектора равна произведению половины дуги сектора на радиус окружности

4) центральный угол (угол, образованный двумя радиусами) измеряется дугой, на которую он опирается;

5) вписанный угол (угол, образованный двумя хордами, исходящими из одной точки окружности) измеряется половиной дуги, на которую он опирается. Вписанный угол, опирающийся на диаметр, – прямой.

Касательная, секущая, хорда и их свойства:

1) касательная к окружности перпендикулярна к радиусу, проведенному в точку касания;

2) отрезки касательных, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности;

3) если AM – касательная к окружности, а CM – секущая, то AM ²= MС ∙ МВ (рис. 10.1);

4) если AM и DM секущие, то AM∙ МВ = МD ∙ MС (рис. 10.2);

5) если точка М есть пересечение двух хорд, то имеет место соотношение AM∙ МВ = МD ∙ MС (рис. 10.3);

6) равные хорды стягивают равные дуги.

 

Рис.10.1. Графическое представление касательной к окружности.

Рис.10.2.Графическое представление секущих АМ и DM

Рис. 10.3. Графическое представление пересечения двух хорд.

Призма.Пусть S – площадь основания призмы; H – высота; V – объем. Справедливы следующие утверждения:

1) объем призмы

2) объем прямоугольного параллелепипеда где a, b, c – длины его ребер, выходящих из одной вершины;

3) объем призмы равен произведению длины бокового ребра призмы на площадь сечения, перпендикулярного боковому ребру.

Пирамида.Пусть S – площадь многоугольника, лежащего в основании пирамиды; H – длина высоты пирамиды; h – длина апофемы боковой грани; P– длина периметра основания; V – объем пирамиды. Справедливы следующие утверждения:

1) площадь боковой поверхности правильной пирамиды

2) объем пирамиды

3) если все боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом, то вершина пирамиды проецируется в центр вписанной в многоугольник основания окружности;

4) если все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то вершина пирамиды проецируется в центр окружности, описанной около многоугольника основания;

5) объём усечённой пирамиды

где S и S₁ – площади оснований усеченной пирамиды.

Цилиндр.Пусть S – площадь боковой поверхности прямого цилиндра; S₁ – площадь полной поверхности цилиндра; R – длина радиуса окружности основания; Н – длина высоты цилиндра; V – объем. Справедливы следующие утверждения:

1) площадь боковой поверхности

2) площадь полной поверхности

3) объем цилиндра

Конус.Пусть S – площадь боковой поверхности прямого конуса; Н – длина высоты кругового конуса; S₁ – площадь полной поверхности конуса; R – длина радиуса окружности основания; l – длина образующей конуса; V – объем. Справедливы следующие утверждения:

1) площадь боковой поверхности

2) площадь полной поверхности конуса

3) объём кругового конуса

4) площадь боковой поверхности усеченного конуса где R и r – длины радиусов оснований усеченного конуса;

5) объём кругового усеченного конуса

Сфера (шар).Пусть R – радиус шара; V – объем шара; S – площадь сферы. Справедливы следующие утверждения:

1) площадь сферы (площадь поверхности шара)

2) объем шара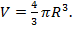

 

Примеры решения задач

Пример 1.Две стороны треугольника равны соответственно 6 и 8 см. Медианы, проведенные к этим сторонам, взаимно перпендикулярны. Найти третью сторону треугольника.

Решение. Дано: ВС = 6 см, АС = 8 см, АF = FC, ВD = DC, BF AD. Найти АВ (рис. 10.4).

Рис. 10.4.Графическое представление задачи.

 

Так как BF и AD – медианы,

то АF = FC = 4 см, ВD = DC = 3 см. К – точка пересечения медиан, поэтому ВК =2KF, АК = 2КD.

Треугольники ВКD, AKF, ABK – прямоугольные.

По теореме Пифагора

Обозначим длины отрезков КD = x, KF = y, тогда АК =2х, ВК =2y, и указанные выше равенства примут вид:

Из полученной системы уравнений найдем АВ:

 

 

Ответ: длина третьей стороны треугольника см.

Пример 2. Внутри равностороннего треугольника взята точка М, отстоящая от его сторон на расстояниях в, с, d. Найти высоту этого треугольника.

Решение. Дано: ∆АВС – равносторонний, MF = a, MD = в, МК = с. MF BC, MK AC, MD АВ.

Найти высоту h треугольника (рис. 10.5).

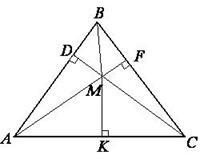
Рис. 10.5. Графическое представление задачи.

Обозначим x – длину стороны треугольника АВС, тогда его площадь

Рассмотрим треугольники ВМС, АМС, ВМА. Их площади соответственно равны:

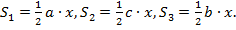
Площадь треугольника АВС равна сумме площадей этих треугольников:

откуда получаем, что

Ответ: высота треугольника

Пример 3. Внутри прямого угла с вершиной С на его биссектрисе взята точка О так, что ОС = Построена окружность радиуса 2 с центром в точке О. Найти площадь фигуры, ограниченной сторонами угла и дугой окружности, заключенной между ними.

Решение. Искомая площадь состоит из площади сектора ОАМВ и удвоенной площади треугольника СОВ (рис. 10.6).

 

Рис. 10.6. Графическое представление задачи.

 

1. Рассмотрим треугольник СОВ. Угол ОСВ равен 45^о, так как СМ – биссектриса.

По теореме синусов:

, т. е. угол СВО равен 30^о.

Значит, угол СОВ равен 105^о, а угол МОВ
как смежный с ним равен 75^о. Для вычисления площади треугольника СОВ воспользуемся формулой :

откуда

Значение можно определить, не используя таблицы, следующим образом:

 

Окончательно

2. Рассмотрим сектор ОАМВ. , где R = 2, а угол АОВ равен 150^о или .

Следовательно, .

Площадь искомой фигуры равна

Ответ:

 

Пример 4. Основанием пирамиды служит равносторонний треугольник со стороной, равной а. Одна из боковых граней – также равносторонний треугольник, перпендикулярный плоскости основания. Определить полную поверхность этой пирамиды.

Решение. Дано: АВС – равносторонний треугольник;

АВ = ВС = АС = а; DСВ – равносторонний треугольник;

СВ = DВ = DС = а; DF – высота пирамиды. DF ВС.

Найти полную поверхность пирамиды (рис. 10.7).

Рис. 10.7. Графическое решение задачи.

Площадь полной поверхности пирамиды равна сумме площадей основания и боковых граней. В основании пирамиды – равносторонний треугольник со стороной а, поэтому его площадь

Площадь треугольника ВСD ,

Опустим из вершины треугольника АВС высоту АF на сторону ВС.

Треугольник АDF – прямоугольный и равнобедренный:

(как высота в равностороннем треугольнике), поэтому DАF = АDF = .

По теореме Пифагора .

Треугольник АDС –равнобедренный, АС = DС = а. Высота СК этого треугольника является медианой и биссектрисой, следовательно, .

Из прямоугольного треугольника КDС по теореме Пифагора найдем КС:

Площадь треугольника АDС

.

Треугольник АDВ равен треугольнику АDС (по трем сторонам), поэтому его площадь .

Площадь полной поверхности:

 

Ответ: площадь полной поверхности пирамиды

Пример 5. Найти объем правильной четырехугольной призмы, если угол между диагональю призмы и боковой гранью равен , а сторона основания равна а.

Решение. Дано: АВСDА₁В₁С₁D₁ –правильная призма,

АВ = ВС = СD = АD = а, АВСD – квадрат, В₁DС₁= .

Найти объем призмы (рис. 10.8).

Рис. 10.8. Графическое представление задачи.

 

Объём призмы V = S H, где S – площадь основания;

Н – высота призмы. В основании призмы лежит квадрат со стороной а (призма – правильная), поэтому .

Треугольник В₁С₁D – прямоугольный, В₁С₁D == .

.

Треугольник С₁СD – прямоугольный,

(по теореме Пифагора).

Объём призмы .

Ответ: объём призмы .