 |
Главная |
Разбивка ЛПО методом прямоугольных координат
|
из
5.00
|
Схема выноски ЛПО методом прямоугольных координат приведена на рисунке 4.1. Переходная кривая АВ выносится в системе координат Х1У1, переходная кривая А'В' – в системе координат Х6У6. Круговая кривая ВВ' делится на четыре части: ВМ, МСО, СОN и NВ'. Эти участки круговой кривой выносятся в системах координат: ВМ – Х2У2, МСО – Х3У3, СОN– Х4У4, NВ'– Х5У5.

1, 2 – оси пересекающихся дорог
Рисунок 4.1 – Схема разбивки ЛПО методом прямоугольных координат
В процессе технических изысканий на местности закреплены оси пересекающихся дорог № 1 и № 2 (рисунок 4.1).
Для выноски систем координат в курсовом проекте приводятся числовые значения требуемых данных в виде таблиц.
Таблица 4.1 – Значения данных для выноски систем координат
| α | R | b1 | b2 | РО1 | С1 | С2 | РК1(А') | РК2(А) | Тд | Тк | β |
Большинство параметров, приведенных в таблице 4.1, определены ранее, за исключением значений Тд и Тк (см. рисунок 4.1):
 ,
,  , (4.1)
, (4.1)
где хВ, уВ – координаты конца переходной кривой, определены по формуле (2.13).
Для расчета координат приводят пикетное положение отрезков кривых плана трассы ЛПО (точек А, В, М, СО, N, В' и А').
Таблица 4.2
| Наименование точек | А | В | М | СО | N | В' | А' |
| Пикетное положение | 0+00 | … | … | … | … | … | … |
Пикетное положение точек М, СО, N получают исходя из условия деления круговой кривой K0 на четыре отрезка:
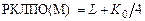 ; (4.2)
; (4.2)
 ; (4.3)
; (4.3)
 . (4.4)
. (4.4)
Расчет координат точек осуществляется с шагом 50 м. В случае расположения точек на переходной кривой координаты х1у1 или х6у6 вычисляют по формулам (2.12), принимая вместо l0 значение расстояния Si от начала координат до точки на кривой.
При расположении точки на круговой кривой координаты х и у вычисляют по формулам
 ,
,  , (4.5)
, (4.5)
где Si – расстояние от начала координат данной системы до рассмат-риваемой точки.
Результаты расчета координат хi и уi сводят в таблицу 4.3.
Таблица 4.3
| Пикетное положение точки | Системы координат | |||||||||||||||||
| х1у1 | х2у2 | х3у3 | х4у4 | х5у5 | х6у6 | |||||||||||||
| S | x | y | S | x | y | S | x | y | S | x | y | S | x | y | S | x | y | |
| 0+50 | … | … | ||||||||||||||||
| 1+00 | … | … | ||||||||||||||||
| 1+50 | … | … | ||||||||||||||||
| 2+00 | … | … | ||||||||||||||||
| 2+50 | … | … | ||||||||||||||||
| … |
Системы прямоугольных координат хiуi на местности получают следующим образом:
Системы х1у1 и х6у6 (см. рисунок 4.1). Трассируют прямые х1 и х6 параллельно осям пересекающихся дорог № 1 и № 2 на расстоянии b1 и b2 от этих осей, закрепленных на местности. По известному пикетному положению РК2(А) и РК1(А') точек А и А' определяют положение начала координат.
Системы х2у2 и х5у5. На осях х1 и х6 откладывают значение Тд от точек А и А' и получают положение точки m и m'. На точку m и m' устанавливают теодолит, по углу β получают направление оси координат х2 (или х5). На направлении х2 (или х5) отмеряют величину Тк и получают начало координат системы х2у2 (или х5у5).
Системы х3у3 и х4у4. На пересечении прямых х1 и х6 получают положение точки Р (рисунок 4.1). Контроль положения точки Р осуществляется с помощью величин С1 и С2. На точку Р устанавливают теодолит, по углу α/2 трассируют направление биссектрисы угла α РО1. На этом направлении отмеряют расстояние (РО1 + R), получают точку СО (середину ЛПО). В точку О устанавливают теодолит и трассируют перпендикулярную к биссектрисе прямую, определяющую направление осей х3 и х4. Оси у3 и у4 направлены по биссектрисе угла α к точке Р.
|
из
5.00
|
Обсуждение в статье: Разбивка ЛПО методом прямоугольных координат |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

