 |
Главная |
Метод эквивалентного генератора
|
из
5.00
|
Метод эквивалентного генератора используется в случае,когда необходимо найти ток, напряжение или мощность в одной ветви. При этом удобно всю остальную часть цепи, к которой подключена данная ветвь, рассматривать в виде двухполюсника [2]. Двухполюсник называют активным, если он содержит источники электрической энергии, и пассивным – в противном случае. На рисунках активный двухполюсник будем обозначать буквой А, а пассивный – П. Различают две модификации метода эквивалентного генератора: метод эквивалентного источника напряжения и метод эквивалентного источника тока.
Метод эквивалентного источника напряжения. Этот метод базируется на теореме Тевенина, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения с задающим напряжением, равным напряжению холостого хода на зажимах разомкнутой ветви, и внутренним сопротивлением, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви (рисунок 1.8).

Рисунок 1.8 – Суть теорем Тевенина и Нортона
После замены активного двухполюсника эквивалентным источником на рисунке 1.8 в соответствии с этой схемой имеем:
i = uxx/(R + Rэ) , (1.40)
где Rэ можно найти либо экспериментальным, либо расчетным путем.
Метод эквивалентного источника тока. В основе этого метода лежит теорема Нортона, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с задающим током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви (рисунок 1.8, в).
Искомый ток можно найти по формуле: i = iкз[Rэ/(R + Rэ)].
Очевидно, что методы эквивалентного источника как напряжения, так и тока дают один и тот же результат.Применение того или иного метода определяется удобством и простотой нахождения uхх или iкз.
Принцип дуальности
Анализ уравнений для напряжений и токов, полученных в предыдущих разделах, позволяет сформулировать важный принцип теории электрических цепей –принцип дуальности (двойственности). Этот принцип гласит: если для данной электрической цепи справедливы некоторые законы, уравнения или соотношения, то они будут справедливы и для дуальных величин в дуальной цепи. Этот принцип проявляется, например, в сходстве законов изменения напряжения в одной цепи и законов изменения токов в другой цепи (дуальной).
Таблица 1.1 иллюстрирует двойственный характер основных законов и соотношений в электрических цепях.
Использование принципа дуальности в ряде случаев позволяет существенно упростить расчет. Так, если найдены уравнения для одной цепи, то, используя дуальные соотношения, можно сразу записать законы изменения дуальных величин в дуальной цепи.
Баланс мощности
Одной из наиболее общих теорем теории электрических цепей является теорема Телледжена. Рассматривая произвольную электрическую цепь, содержащую nв ветвей и nу узлов, для согласованных направлений напряжений и токов ветвей теорема Телледженагласит [2]: сумма произведений напряжений uk и токов ik всех ветвей цепи, удовлетворяющих законам Кирхгофа, равна нулю:
 . (1.41)
. (1.41)
Таблица 1.1 – Двойственный характер соотношений в электрических цепях
| Понятия | |
| исходные | дуальные |
| Напряжение u Сопротивление R Задающее напряжение uГ | Ток i Проводимость G Задающий ток iГ |
ЗТК:  u = Ri;
u = Ri; 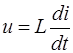
 Метод контурных токов.
Метод эквивалентного генератора
напряжения.
Метод контурных токов.
Метод эквивалентного генератора
напряжения.
| ЗНК:  i = Gu;
i = Gu; 
 Метод узловых напряжений.
Метод эквивалентного генератора
тока.
Метод узловых напряжений.
Метод эквивалентного генератора
тока.
|
Последовательное:
 ; ;
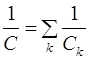 . .
| Параллельное:
 ; ;
 . .
|
Необходимо подчеркнуть, что поскольку теорема Телледжена следует непосредственно из законов Кирхгофа, то она справедлива для любых электрических цепей: линейных и нелинейных, активных и пассивных, цепей, параметры которых изменяются во времени (параметрических цепей).
Из теоремы Телледжена вытекает ряд следствий, важнейшим из которых является баланс мощности. Действительно, произведениеukik представляет собой мгновенную мощностьрk k-й ветви, поэтому сумма мощностей всех ветвей цепи равняется нулю.
Если выделить ветви с независимыми источниками, то баланс мощности можно сформулировать следующим образом: сумма мощностей, отдаваемых независимыми источниками, равняется сумме мощностей, потребляемых остальными ветвями электрической цепи.
При определении Рист произведение uгi берется со знаком «+», если направления задающего напряжения uг и тока i направлены навстречу друг другу, и со знаком «–» в противном случае. Аналогичное правило знаков для источников тока: если напряжение на зажимах источника направлено навстречу задающему току iг берется знак «+», а если напряжение совпадает с током – знак «–». Баланс мощности выражает закон сохранения энергии в электрической цепи.
Одной из важнейших практических задач является оптимальная передачаэлектрической энергии от активного к пассивному двухполюснику. Оптимум обычно понимается в смысле получения максимальной мощности в нагрузке Rн. Для цепи постоянного тока активный и пассивный двухполюсники можно заменить эквивалентной схемой, изображенной на рисунке 1.9.

Рисунок 1.9 – Активный и пассивный двухполюсники
Мощность p определим с помощью выражения:
pн = i2Rн = (uг2)Rн / (Rг + Rн)2 .(1.42)
Напряжение на нагрузке uн = uг - iRг. Максимум мощности будет достигаться при Rн = Rг, при этом ток в цепи принимает значение io = = uг/(2Rг), а мощность рн max = uг2/(4Rг).
Коэффициент полезного действия системы передачи определяется равенством:
h = рн/рист = (uгi - i2Rг) / (uгi) = 1 - iRг/uг . (1.43)
При i = io и pн = pн max имеем h =0,5 (50 %). На рисунке 1.10 представлены зависимости рист, рн и h от тока i.

Рисунок 1.10 – Зависимости мощностей, выделяющихся на источнике и нагрузке при Rн = Rг
Вопросы для самотестирования
1 Закон Кирхгофа для токов гласит: алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Но применим ли этот закон для цепи, в одной из ветвей которой ток в её начале имеется, а на её конце ток равен нулю?
2 Справедливы ли законы токов и напряжений Кирхгофа для метода контурных токов?
3 Теорема Телледжена гласит: сумма произведений напряжений uk и токов ik всех ветвей цепи, удовлетворяющих законам Кирхгофа, равна нулю. Справедлива ли она для линейных, нелинейных, активных и пассивных цепей?
4 Для нахождения тока в одной и той же ветви электрической цепи сначала использован метод эквивалентного источника напряжения, а затем метод эквивалентного источника тока. Чем будут отличаться результаты, полученные в обеих случаях?
5 Как называются две электрические цепи, если существует сходство изменения напряжения в одной цепи и законов изменения токов в другой цепи (u = Ri и i = Gu)?
|
из
5.00
|
Обсуждение в статье: Метод эквивалентного генератора |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

