Символический метод расчёта при гармоническом воздействии

Расчет разветвленных цепей при смешанном соединении элементов в режиме гармонических воздействий обычно осуществляется символическим методом. Это объясняется тем, что классический метод расчета приводит к громоздким интегрально-дифференциальным уравнениям и требует большого объема тригонометрических преобразований. Символический метод позволяет тригонометрические операции над гармоническими колебаниями и геометрические операции над векторами свести к алгебраическим операциям над комплексными числами, что существенно упрощает расчет. При этом могут быть использованы все методы преобразований и анализа, изложенные ранее.

Допустимость использования символического метода объясняется тем, что в линейных цепях в режиме гармонических воздействий в цепи устанавливаются гармонические колебания той же частоты.Таким образом, неизвестными параметрами токов и напряжений будут лишь амплитуды и фазы, определяемые однозначно их комплексными амплитудами ( ). Запишем основные законы электрических цепей в символической форме.

Для резистивного элемента R связь между комплексными амплитудами тока и напряжения можно определить, согласно закону Ома, путем замены мгновенных значений токов i и напряжений u их комплексными амплитудами:

. (1.61)

Для индуктивного элемента L связь между и 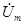(с учётом, что ) определится:

; , (1.62, 1.63)

гдe j = e^jp/2 – (из формулы Эйлера) множитель, характеризующий фазовый сдвиг между вектором тока и напряжением 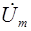. Уравнение отражает закон Ома для индуктивных элементов.

Для емкостного элемента С можно записать (с учётом, что ):

или 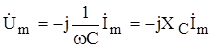. (1.64, 1.65)

Аналогично можно получить уравнения законов Кирхгофа в комплексной форме. Так, для ЗТК, заменив мгновенные значения токов i_k их комплексными амплитудами , получим:

, а для 3HK: 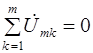. (1.66, 1.67)

Полученные уравнения законов Ома и Кирхгофа в комплексной форме лежат в основесимволического метода расчета линейных цепей при гармонических воздействиях. Причем при переходе к комплексной записи операции дифференцирования d/dt заменяются умножением на jw , операции интегрирования – делением на jw.В результате вместо системы интегрально-дифференциальных уравнений получаем систему алгебраических уравнений, решение которой определяет амплитуды и начальные фазы искомых токов и напряжений. Например:

; (1.68)

. (1.69)

При анализе различных электрических цепей часто возникает необходимость преобразования схемы последовательно соединенных элементов в эквивалентное параллельное соединение и наоборот (рисунок 1.16).

Рисунок 1.16 – Преобразование соединений элементов

В основе подобных преобразований лежит принцип эквивалентности. Согласно этому принципу? ток i и напряжение u в исходной и преобразованной схемах должны остаться неизменными. Для первой схемы 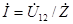, для второй . Из равенства токов и напряжений для обеих схем имеем:

. (1.70)

Из этого равенства (1.80) следуют формулы преобразования параллельного участка в эквивалентный последовательный:

R = G/Y² ; X = B/Y² . (1.71, 1.72)

Аналогично из равенства можно получить формулы преобразования последовательного участка в эквивалентный параллельный: