 |
Главная |
Преобразование электрических схем
|
из
5.00
|
Преобразования электрических схем применяются для упрощения расчетов. Наиболее типичные методы преобразования следующие.
Последовательное соединение элементов. Согласно ЗТК при последовательном соединении элементов через них протекает один и тот же ток (рисунок 1.2).

Рисунок 1.2 – Последовательное соединение элементов
Согласно ЗНК, напряжение, приложенное ко всей цепи:
 . (1.13)
. (1.13)
Тогда для последовательного соединения резистивных элементов R1, R2, ..., Rn будем иметь формулу:
 . (1.14)
. (1.14)
Для последовательного соединения индуктивных элементов (рисунок 1.2):
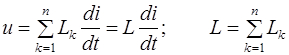 . (1.15)
. (1.15)
Для последовательного соединения емкостных элементов:
 . (1.16)
. (1.16)
При n = 2: С = С1C2/(С1 + С2). (1.17)
При последовательном соединении независимых источников напряжения они заменяются эквивалентным источником напряжения с задающим напряжением uГ, равным алгебраической сумме напряжений отдельных источников. Причем со знаком «+» берутся напряжения, совпадающие с задающим напряжением эквивалентного источника, а со знаком «–» – не совпадающие (рисунок 1.3).

Рисунок 1.3 – Последовательное соединение источников напряжения
Параллельное соединение элементов. При параллельном соединении элементов, согласно ЗНК, к ним будет приложено одно и то же напряжение (рисунок 1.4). Согласно ЗТК, для тока каждой из схем, изображенных на рисунке 1.4, можно записать:
 . (1.18)
. (1.18)

Рисунок 1.4 – Параллельное соединение пассивных элементов
На основании этого уравнения для параллельного соединения резистивных элементов получаем:
 . (1.19)
. (1.19)
Для параллельного соединения емкостных элементов:
 . (1.20)
. (1.20)
Для параллельного соединения индуктивных элементов:
 . (1.21)
. (1.21)
Следовательно, цепь из n параллельно соединенных резистивных, индуктивных или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом.
В частности, при n = 2:
R = R1R2/(R1 + R2); L = L1L2/(L1 + L2) . (1.22)
Параллельно соединенные независимые источники тока можно заменить одним эквивалентным источником тока с задающим током, равным алгебраической сумме задающих токов отдельных источников. Причем со знаком «+» берутся задающие токи, совпадающие по направлению с задающим током эквивалентного источника, а со знаком «–» – не совпадающие (рисунок 1.5).

Рисунок 1.5 – Параллельное соединение источников тока
При расчете электрических цепей часто возникает необходимость преобразования источника напряжения с параметрами uг и Rг, в эквивалентный источник тока с параметрами iг и Gг, или наоборот – преобразование источника тока в эквивалентный источник напряжения. Эти преобразования осуществляются в соответствии с формулами:
iг = uг/Rг ; Gг = 1/Rг . (1.23)
Принцип наложения
Принцип наложения (суперпозиции) имеет важнейшее значение в теории линейных электрических цепей. Если рассматривать напряжения и токи источников как задающие воздействия, а напряжение и токи в отдельных ветвях цепи как реакцию (отклик) цепи на эти воздействия, то принцип наложения можно сформулировать следующим образом: реакция линейной цепи на сумму воздействий равна сумме реакций от каждого воздействия в отдельности.Принцип наложения можно использовать для нахождения реакции в линейной цепи, находящейся под воздействием нескольких источников.
Рассмотрим случай, когда в линейной цепи действует несколько источников. В соответствии с принципом наложения для нахождения тока i или напряжения u в заданной ветви осуществим поочередное воздействие каждым источником и найдем соответствующие частные реакции ik и uk на эти воздействия. Тогда результирующая реакция определится как
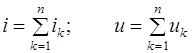 , (1.24)
, (1.24)
где n – общее число источников.
При определении результирующих токов знак «+» берут у частных токов, совпадающих с выбранным положительным направлением результирующего тока, и знак «–» – у несовпадающих. При составлении частичных электрических схем исключаемые идеальные источники напряжения закорачиваются. В случае, если в цепи действуют источники напряжения с внутренними сопротивлениями RГ, при их исключении они заменяются своими внутренними сопротивлениями RГ.
При наличии идеальных источников тока соответствующие ветви исключаемых источников размыкаются, а при наличии реальных источников они заменяются своими внутренними проводимостями GГ.
Если в линейной цепи приложено напряжение сложной формы, применение принципа наложения позволяет разложить это воздействие на сумму простейших и найти реакцию цепи на каждое из них в отдельности с последующим наложением полученных результатов.
Вопросы для самотестирования
1 Чем отличается параметр электрической цепи «сопротивление» от элемента электрической цепи «резистор»?
2 В каком элементе электрической цепи энергия запасается в магнитном поле?
3 Может ли мгновенная мощность электрического поля ёмкости быть отрицательной?
4 Как может быть реализован идеализированный источник напряжения «ег»?
5 Закон Кирхгофа для токов гласит: алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Но применим ли этот закон для цепи, где токи в ветвях описываются однородными линейными алгебраическими уравнениями с постоянными коэффициентами?
Метод контурных токов
При определении токов и напряжений в отдельных ветвях цепи с nВ-ветвями по законам Кирхгофа в общем случае необходимо решить систему из nВ уравнений. Для снижения числа решаемых уравнений и упрощения расчетов используют метод контурных токов и узловых напряжений [2]. Метод контурных токов позволяет снизить число решаемых уравнений до числа независимых контуров. В его основе лежит введение в каждый контур условного контурного тока iк, направление которого обычно выбирают совпадающим с направлением обхода контура. При этом для контурного тока будут справедливы ЗТК и ЗНК. В частности, для каждого из выделенных контуров можно составить уравнения по ЗНК. Рассмотрим резистивную цепь, схема которой изображена на рисунке 1.6.
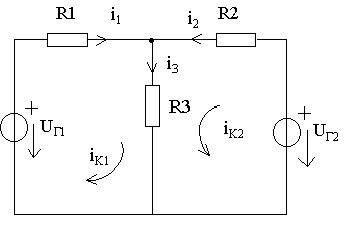
Рисунок 1.6 – Иллюстрация метода контурных токов
Для контурных токов iк1 и iк2 этой схемы можно записать уравнения по ЗНК в виде:
–uг1 + (R1 + R3)iк1 + R3iк2 = 0 ; (1.25)
–uг2 + R3iк1 + (R2 + R3)iк2 = 0. (1.26)
Перенесем uГ1 и uГ2 в правую часть системы и получим так называемую каноническую форму записи уравненийпо методу контурных токов:
R11iк1 + R12iк2 = uк1 , (1.27)
R21iк1 + R22iк2 = uк2 , (1.28)
где R11 = R1 +R3; R22 = R2 + R3 называют собственными или контурными сопротивлениями 1-го и 2-го контуров; R12 = R21 = R3 – взаимным сопротивлением 1-го и 2-го контуров; uк1 = uг1; uк2 = uг2 – контурными задающими напряжениями. Истинные токи в ветвях находятся как алгебраическая сумма контурных токов: i1 = iк1, i2 = iк2, i3 = = iк1 + iк2.
Решая систему уравнений, находят величины контурных токов:
iк1 = D1/DR ; iк2 = D2/DR ; iкk = Dk/DR , (1.29)
где DR - определитель системы:
 . (1.30)
. (1.30)
Определитель Dk находится путем замены k-го столбца правой частью приведённой выше системы. Например, для D1имеем:
 . (1.31)
. (1.31)
Полученный результат отражает рассмотренный ранее принцип наложения.
Для линейных электрических цепей важную роль играет принцип взаимности (теорема обратимости). Он гласит: если источник напряжения, помещенный в какую-либо ветвьl пассивной линейной электрической цепи, вызывает в другой ветви k ток определенной величины, то этот же источник, будучи помещенным в ветвь k, вызывает в ветвиl ток той же величины. Справедливость этого принципа следует непосредственно из уравнений ikk с учетом того, что Dlk = Dkl.
|
из
5.00
|
Обсуждение в статье: Преобразование электрических схем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

