Обратное преобразование Лапласа

Обратное преобразование Лапласа позволяет получить оригинал функции по его изображению :

(1.12)

Использование этого выражения весьма затруднительно, особенно, для сложных выражений 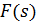. Поэтому были разработаны более приемлемые способы определения оригинала , в основе которых лежат вычеты. В теории автоматического управления применяют обычно два способа решения поставленной задачи.

Первый метод связан с использованием выражения

(1.13)

где - полюсы функции .

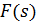В общем случае, когда имеется mкратных полюсов вычет по кратному полюсу определяется по следующему соотношению:

. (1.14)

В частном случае при m=2 имеем:

(1.15)

а при m=1 получаем простое соотношение:

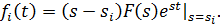(1.16)

Пример 1.14. Пусть операторное изображение функции равно 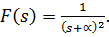Отсюдаимеем два кратных корня: .Используя соотношение(1.15), получим:

Таким образом получим очевидный (по таблице Лапласа) результат.

Пример 1.15. Пусть

Так как полюсы некратные, для определения вычетов можно воспользоваться соотношением(1.16):

Пример 1.16. Найти оригинал , соответствующий изображению

.

Вычисление полюсов показывает, что они некратные, но комплексно-сопряжённые: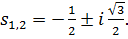

В реальных задачах случай комплексных полюсов встречается довольно часто. Таким образом имеем

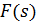Второй способ получения оригинала по его изображению сводится к разложению 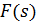на элементарные составляющие:

(1.17)

где - полюсы, q - вещественный остаток; - коэффициенты, определяемые с помощью вычетов.

Если имеется полюс кратности m, то разложение на простые дроби включает члены

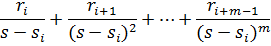. (1.18)

Определение вычетов, особенно, для кратных корней является довольно трудоёмкой процедурой. Поэтому в инженерной практике в настоящее время для решения этой задачи обычно используют функции MatLabresidue(). Она имеет следующий синтаксис:

[r,p,q]=residue (b,a),

где r - вектор-столбец вычетов;

p - вектор-столбец полюсов;

q -вещественная часть разложения;

b, a - соответственно массивы коэффициентов полиномов числителя и знаменателя F(s).

Пример 1.17.Пусть

Для получения оригинала воспользуемся методом разложения на элементарные составляющие. Порядок знаменателя равен двум, поэтому

Определение полюсов и коэффициентов будем осуществлять с помощью функцииresidue:

>>[r,p,q]=residue([2],[1,7,12])

В результате будет получено:

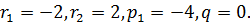
Теперь можно записать выражение F(s) в общепринятой форме:

Для получения оригинала воспользуемся таблицей преобразования Лапласа:

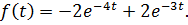
В пакете MatLab имеется ещё одна специальная функция ilaplace(), позволяющая сразу получить оригинал функцииf(t) по её изображениюF(s). Она имеет следующий синтаксис:

f=ilaplace(Fs)

f=ilaplace(Fs,y)

f=ilaplace(Fs,y,x).

Для её использования необходимо объявлять символьные переменные (y,x).

Пример 1.18. Решим пример 1.17 с помощью функции ilaplace.

>>symss % объявление символьных переменных

>>Fs=2/(s^2+7*s+12);

>>f=ilaplace(Fs)

>>f=2/exp(3*t)-2/exp(4*t)

Таким образом, получен такой же результат, как и в примере 1.17: