Расчётные модели в пространстве состояний

Основными элементами РМ являются:

1) интеграторы (рис. 4.2);

2) умножители (рис. 4.3);

3)

		Рис. 4.2		Рис. 4.3		Рис. 4.4

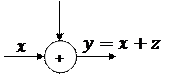Расчётные модели обычно строятся на основе дифференциальных уравнений динамических объектов и систем. Существует несколько приёмов (подходов) получения РМ и соответствующих этой модели уравнений (4.1), (4.2). Рассмотрим один из них, называемый методом последовательного интегрирования наивысшей производной, на примере построения РМ электродвигателя постоянного тока независимого возбуждения, заданного дифференциальным уравнением

,

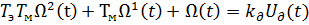где - соответственно скорость вращения двигателя и напряжение якорной цепи.

Разрешим это уравнение относительно второй производной:

Выстроим цепочку из двух интеграторов с сумматором на входе первого слева интегратора. Затем добавим каналы суммирования фазовых координат ( , ) согласно уравнению (4.3). В результате получим РМ, представленную на рис. 4.5.

Рис. 4.5

Обозначим выходы интеграторов символами переменных состояния: С целью стандартизации записи уравнений состояния в форме (4.1) 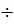(4.2), положим 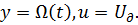Тогда на основе построенной РМ (рис. 4.5) получим:

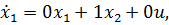
Отсюда в матричной форме имеем

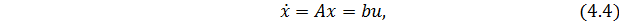
где

Система уравнений (4.4) 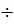(4.5) является стандартной формой уравнений состояния для системы с одним входом и одним выходом. Это частный случай уравнений (4.1), (4.2), в которых матрицы вырождаются в соответствующие вектор-столбец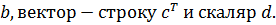

Если задана структурная схема САУ с ПФ её звеньев, то для каждого звена можно построить расчётные модели, а затем соединить их согласно схеме системы.

Рассмотрим эту методику на примере. Пусть задана структурная схема рассмотренного выше электродвигателя постоянного тока (рис. 4.6),

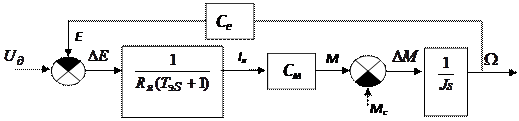Рис. 4.6

где R_я – сопротивление якорной цепи, – момент инерции якоря, I_я – ток якоря, Е – ЭДС внутренней обратной связи по , С_e и С_м - коэффициенты пропорциональности.

Необходимо получить уравнения состояния для данной структуры, при этом в качестве входных координат использовать напряжение питания и момент сопротивления , а в качестве выходных координат взять скорость вращения электродвигателя и развиваемый им момент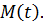

В приведённой структуре динамическими элементами являются два блока, описываемые следующими ПФ:

Поэтому для получения РМ электродвигателя достаточно построить расчётные модели этих блоков, а затем соединить все частные РМ в соответствии со структурной схемой ЭД (рис. 4.6).

По ПФ можно определить эквивалентное дифференциальное уравнение

Разделив его относительно производной получим

Используя методику последовательного интегрирования старшей производной, можно построить РМ, приведённую на рис. 4.7.

Рис. 4.7

Аналогично можно построить РМ для . Она представлена на рис. 4.8.

Рис. 4.8

Для других звеньев расчётные модели имеют вид простых умножителей и сумматоров.

Таким образом, используя полученные РМ можно построить комбинированную РМ системы в целом (рис. 4.9). Здесь в качестве переменных состояния выбраны также выходы интегралов; при этом индексация переменных состояния может осуществляться в произвольном порядке.

Рис. 4.9

На основе комбинированной РМ можно записать систему двух уравнений состояния относительно первых производных :

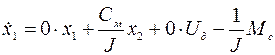(4.6)

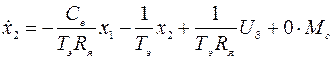(4.7)

Согласно заданию для выходных координат имеем

(4.8)

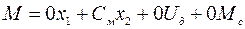(4.9)

Отсюда, сравнивая структуру уравнений (4.1) - (4.2) с уравнениями (4.6) 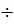(4.9) можно записать

, , ,

, , , .

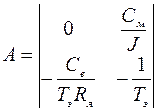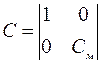Если в качестве входного воздействия взять одно напряжение 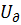и один выход , то система уравнений состояния будет иметь вид (4.4) 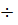(4.5). При этом структура матрицы 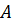не изменится, а матрицы вырождаются в соответствующие векторы:

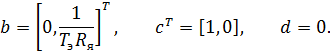
Следует отметить, что несмотря на различие в переменных состояния полученные в рассмотренных примерах уравнения состояния эквивалентны относительно координат вход – выход.

В большинстве своём исходные дифференциальные уравнения САУ содержат в правой части производные (или передаточные функции имеют числитель с порядком отличным от нуля). В этом случае метод последовательного интегрирования старшей производной для инженерной практики не подходит, т.к. требуется производить пересчёт начальных условий на интеграторах РМ по довольно сложным соотношениям.

Выход находят в использовании так называемых типовых (канонических) форм РМ.

Типовые расчётные модели имеют регулярные структуры, что значительно упрощает получение уравнений и состояния динамических систем.

До настоящего времени ещё нет единства в обозначении данных форм, хотя большинство специалистов склоняется использовать терминологию В. Стрейца []. Поэтому в дальнейшем будем придерживаться названий типовых РМ по Стрейцу.

Для решения выше указанной проблемы используются две канонические формы РМ:

· каноническая форма восстанавливаемости (КФВ);

· каноническая форма управляемости (КФУ).

Рассмотрим эти модели более подробно.