 |
Главная |
Векторы и линейные пространства
|
из
5.00
|
Векторы
Ранее было дано определение вектору как матрице размером n*1 – вектор-столбец x и как матрица размером 1*n – вектор-строка  , где n – размерность вектора. Если n = 3, то вектору можно дать геометрическую интерпретацию в трёхмерном пространстве, если
, где n – размерность вектора. Если n = 3, то вектору можно дать геометрическую интерпретацию в трёхмерном пространстве, если 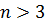 , то геометрическое представление утрачивает свой смысл, однако терминология, связанная с привычными координатными системами, оказывается весьма полезной. Например, системы координат с единичными векторами
, то геометрическое представление утрачивает свой смысл, однако терминология, связанная с привычными координатными системами, оказывается весьма полезной. Например, системы координат с единичными векторами
 ,
,  , …
, …  ,
,
может воображаться в виде n – мерной системы с взаимно ортогональными координатными осями.
Над векторами можно осуществлять ряд характерных для них операций и преобразований. Будем рассматривать далее только действительные векторы.
Скалярное произведение двух векторов x и y записывается и определяется как

Скалярное произведение используется часто для проверки ортогональности векторов: два вектора x и y называются ортогональными, если (y,x) = (x,y)=0.
Например, для векторов 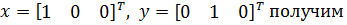

Внешнее произведение осуществляется согласно правилу

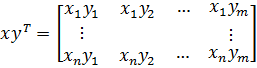 ,
,
где x, y – соответственно векторы с размерностью n*1 и m*1.
Эта операция встречается очень редко, обычно при преобразовании некоторых векторно-матричных соотношений.
Довольно часто требуется оценить длину вектора x. Она получила название нормы  , которая определяется как квадратный корень от скалярного произведения векторов x и x:
, которая определяется как квадратный корень от скалярного произведения векторов x и x:
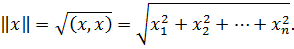
Следствием этого выражения является два соотношения:
 - неравенство треугольника;
- неравенство треугольника;
 – неравенство Шварца.
– неравенство Шварца.
Вектор называется единичным или нормированным, если его длина равна единице, т.е. (x,x)=1. Операция нормирования осуществляется с делением вектора на его норму:

Пример 3.6. Произвести нормирование вектора 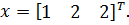


Проверка: 
Очень важным свойством векторов является их линейная независимость. Векторы  называются линейно независимыми, если не выполняется равенство
называются линейно независимыми, если не выполняется равенство
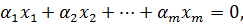
где  – числа, среди которых по крайней мере одно число не равно нулю.
– числа, среди которых по крайней мере одно число не равно нулю.
Если это равенство справедливо только при всех  то такая система векторов является линейно независимой.
то такая система векторов является линейно независимой.
Для оценки линейной независимости векторов вычисляется определитель матрицы, составленный из векторов  в следующей форме:
в следующей форме:
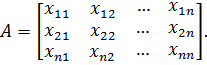 (3.9)
(3.9)
Необходимым и достаточным условием линейной независимости векторов  является равенство ранга матрицы A величине n.
является равенство ранга матрицы A величине n.
Пример 3.7. Оценить свойство линейной независимости системы векторов
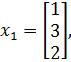
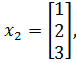

Построим и вычислим определитель матрицы A (3.9):

Таким образом, заданная система векторов линейно независима, т.к. ранг матрицы 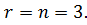
|
из
5.00
|
Обсуждение в статье: Векторы и линейные пространства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

