Операторы физических величин. Средние значения

Чтобы записать уравнениеШредингера (1926), рассмотрим сначала схему вывода дисперсионного уравнения для плоской монохроматической волны:

исходное волновое уравнение:

, (2.1)

решение – плоская волна:

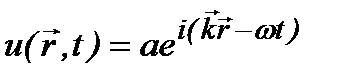, (2.1a)

Отсюда следует дисперсионное уравнение, связывающее частоту и волновое число плоской волны (2.1а):

. (2.2)

Чтобы записать уравнение Шредингера для волновой функции, воспользуемся схемой (2.1-2.2), идя «снизу вверх» – от (2.2) к (2.1). «Дисперсионным уравнением», связывающим частоту и волновой вектор волн де Бройля, является формула для полной энергии частицы:

, (2.5)

где – потенциальная энергия частицы, – функция Гамильтона. Действительно, пользуясь соотношениями (1.49), (1.50), из (2.5) получаем:

. (2.5а)

Умножим формально обе части (2.5а) на волновую функцию:

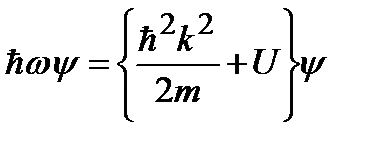. (2.5б)

Заменяем затем и на операторы согласно (2.3а), (2.4а). Тогда приходим к искомому уравнению Шредингера:

, (2.6)

где величина

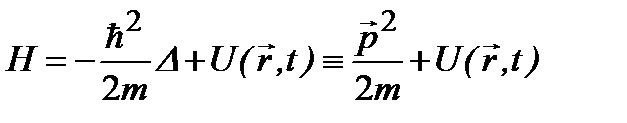(2.7)

оператор Гамильтона, или гамильтониан. оператор импульса:

.(2.8)

Уравнение (2.6) - нестационарное уравнение Шредингера.

Если потенциальная энергия не зависит от времени, то оператор Гамильтона (2.7) зависит только от координат. В этом случае состоянияквантовой системы называются стационарными. Для таких состояний пространственная и временная зависимости в волновой функции могут быть разделены: . Тогда из (2.6) получаем: , где Е – постоянная разделения, имеющая смысл энергии состояния. Отсюда следует, что временная зависимость волновой функции согласно уравнению является вполне определенной: . Пространственная зависимость волновой функции описывается уравнением:

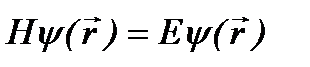. (2.9)

Таким образом, для стационарных состояний волновая функция имеет вид:

. (2.10)

Плотность вероятностей таких состояний не зависит от времени: . Поэтому они называются стационарными. Уравнение (2.9) - стационарное уравнение Шредингера, которое часто записывают в эквивалентной форме:

. (2.11)

Уравнение Шредингера линейно относительно волновой функции. Поэтому справедливпринцип суперпозиции решений.

. (2.12)

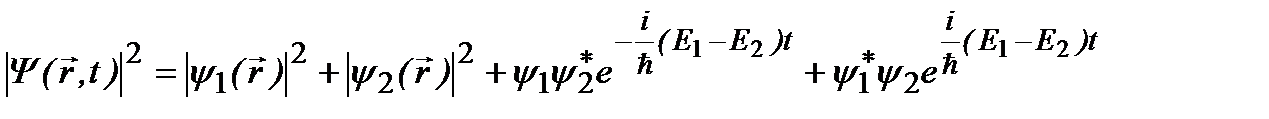. (2.12a)

Условие нормировки волновой функции вытекает из уравнения Шредингера: умножая уравнение (2.8) слева на функцию , а комплексно–сопряженное уравнение – на 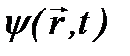, и затем, вычитая полученные выражения, приходим к уравнению:

.

Вектор (2.13)

интерпретируется как вектор плотности потока вероятности. Таким образом, приходим к уравнению, имеющему смысл уравнения сохранения вероятности:

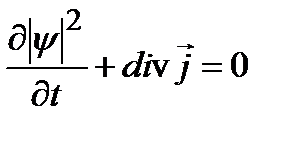. (2.13a)

Волновая функция должна быть однозначной, непрерывной и ограниченной вместе со своими первыми производными.

Уравнение Шредингера является нерелятивистским и не учитывает важного свойства микрочастиц – их спина.

Уравнение Шредингера в форме (2.9) показывает, что в результате воздействия оператора Гамильтона (2.7) на волновую функцию получается та же волновая функция, помноженная на постоянное значение энергии. Тогда говорят, что поставлена задача на собственные значения оператора, в данном случае, оператора Гамильтона. При соблюдении физических требований на волновую функцию и при соответствующих граничных условиях решение этой задачи существует не при любых значениях постоянной Е, а лишь при строго определенных значениях, образующих энергетический спектр рассматриваемой системы: Эти значения называются собственными значениями энергии, а соответствующие им волновые функции называются собственными функциями.Квадрат модуля собственной волновой функции 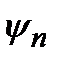определяет плотность вероятности того, что квантовая система находится в элементе объема dV вблизи точки в состоянии со значением энергии .

Вместе с формулой (2.14а) полученное соотношение может быть записано единым образом как условие ортонормировкисобственных волновых функций:

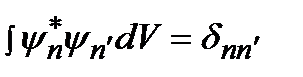, (2.14)

где – символ Кронекера: .

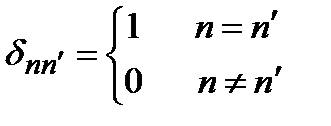Если F – некоторая физическая величина, то ей сопоставляется оператор , для которого аналогично (2.9) ставится задача на собственные значения. Эти собственные значения образуют спектр величины F. В общем спектр может быть дискретным, составленным из дискретных значений , и может быть непрерывным,простирающимся по всей области задания величины F. Для удовлетворения принципу суперпозиции квантовые операторы должны быть линейными. Такие операторы определяются условиями: ( + ) = = + , (а )=а , где , 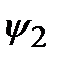– произвольные функции, а – произвольная постоянная.

В случае дискретного спектра задача на собственные значения ставится аналогично (2.9):

. (2.15)

Собственные функции удовлетворяют условию ортонормировки (2.14). Если квантовая система описывается произвольной волновой функцией 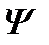, то в результате измерения величины F должно получиться одно из собственных значений , которому соответствует собственная функция . Отсюда следует, согласно принципу суперпозиции, что волновая функция , в общем, должна быть представлена в виде линейной комбинации собственных функций оператора :

, (215а)

Величину можно интерпретировать как вероятность того, что величина F имеет значение .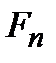

Среднее значениевеличины F определяется по общим правилам теории вероятностей как сумма собственных значений, умноженных на соответствующую им вероятность:

. (2.17)

Преобразуем это выражение, используя соотношения (2.16а), (2.15), (2.15а):

.

Когда система находится в состоянии, описываемом собственной волновой функцией, то среднее значение величины F совпадает с его собственным значением:

.

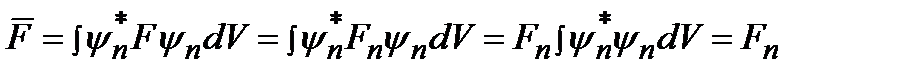В этом случае говорят, что оператор – эрмитов оператор. Более общее условие эрмитовости оператора определяется соотношением:

,

где 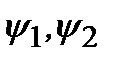– произвольные функции. Таким образом, операторы физических величинв квантовой механике должны быть линейнымииэрмитовыми.

Если 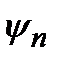– общая собственная функция операторов и , то 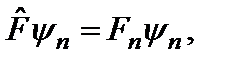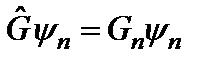. Подействуем теперь на первое их этих соотношений оператором , а на второе соотношение – оператором . В результате полу-чаем:

.

Отсюда следует: . Это соотношение записывается в виде символического равенства:

.

Если операторы имеют общие собственные функции, то они коммутируют друг с другом.Справедливо также обратное утверждение: если операторы коммутируют, то они имеют общие собственные функции.Физически это означает, что соответствующие физические величины могут одновременно иметь определенные измеряемые значения.

Разность называют коммутатором операторов и .

Волновые функции системы обладают четностью. Это свойство связано с преобразованием инверсии - изменение знаков всех декартовых координат на обратные: 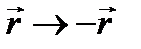. В соответствии с преобразованием инверсии вводят оператор инверсии , который изменяет знаки координат волновой функции на обратные: 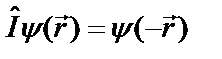. Существуют волновые функции, которые не изменяют своего знака при инверсии координат: , есть также волновые функции, изменяющие свой знак: . Первые функции называются четными, а вторые – нечетными. Говорят также о функциях, соответственно, с положительнойи отрицательной четностью.