Лекция 10. Потенциальные «ямы» и «барьеры»

Стационарное уравнение Шредингера (2.11) в одномерном случае имеет вид:

. (2.20)

Состояния движущейся частицы зависят от характера ее потенциальной энергии .

В каждой из областей оси x, где потенциальная энергия постоянна, можно найти точное решение уравнения (2.20). Характер решения зависит от знака величины . Например, в случае свободной частицы, потенциальная энергия которой равна нулю, волновая функция, как решение уравнения (2.20), описывает волны типа , бегущие в положительном (знак плюс) или отрицательном (знак минус) направлении оси х, где волновое число 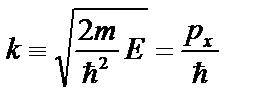.При этом надо помнить о временном множителе . Если потенциальная энергия частицы не равна нулю, то при (полная энергия частицы превышает потенциальную энергию) решение также представляет собой волны, бегущие в противоположных направлениях. В случае (т.е. E<U) общее решение содержит комбинации решений вида 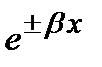, где .

Рассмотрим подробнее модель прямоугольной ямы. Простейшей является задача о частице в потенци-альном ящике. В этом случае потенциальная энергия равна нулю на некотором отрезке оси x от 0 до , и скачком обращается в бесконечность на концах этого отрезка (рис.2.5). Частица оказывается запертой на этом отрезке и не может выйти за его пределы. Такой характер потенциальной энергии описывается формулой:

Рис.2.5

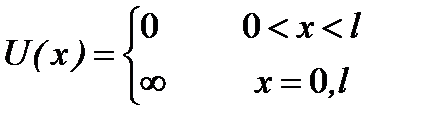. (2.21)

Найдем граничные условия для волновой функции. Обозначая 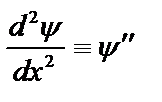, из (2.20) получим:

. (2.21a)

При правая часть в (2.21а) согласно (2.21) обращается в бесконечность. Так как волновая функция и ее производные не могут принимать бесконечно большие значения, то в этих точках должна обращаться в нуль волновая функция:

. (2.22)

. (2.23)

, (2.24)

где A,B – постоянные, определяемые граничными условиями и условием нормировки. Из граничных условий (2.22) следует: . Таким образом,

, (2.24a)

где число 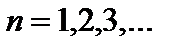Значение n = 0 исключается

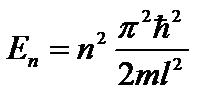. (2.25)

Необходимо еще найти собственные функции. Согласно (2.24), (2.24а) собственные функции c cобственными значениями энергии (2.25) определяются формулой

. (2.27)

Эти функции образуют ортонормированную систему, т.е. они удовлетворяют условию (2.14):

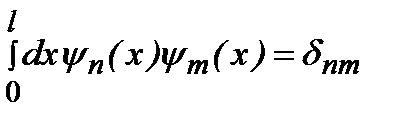, (2.28)

Постоянная определяется из условия нормировки:

. (2.28a)

Отсюда . Таким образом, ортонормированная система собственных функций частицы в потенциальном ящике описывается формулой:

. (2.29)

Собственные функции с энергией равны 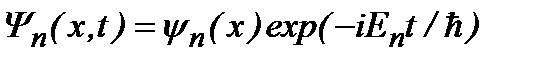. По общим правилам, выражение

(2.30)

Допустим, что частица падает на барьер слева направо с энергией . Тогда при достижении точки классическая частица полностью отразилась бы от барьера. Для нее область «запрещена». Для квантовой частицы, однако, имеется отличная от нуля вероятность обнару-жить ее и в «запрещенной» области (рис.2.7). Этот эффект анало-гичен известному в оптике явлению полного внутреннего отра-жениясвета на границе раздела двух разных сред. С увеличением высоты потенциального барьера область «просачивания» частицы уменьшается и при стремится к нулю. В этом случае волновая функция при обращается в нуль. Если , то классическая частица проходит такой барьер без всякого отражения. В квантовом же случае наряду с проходящей волной де Бройля имеется также отраженная от барьера волна, и можно вычислить соответствующий коэффициент отражения. Если ширина барьера конечна (рис.2.4б) и энергия падающей слева частицы меньше высоты барьера, то возникает чисто квантовый эффект просачивания частицы сквозь барьер – туннельный эффект.

При рассмотрении барьерных задач важную роль играют коэффициент отраженияот барьера и коэффициент прозрачностибарьера. Коэффициент отражения определяется как отношение плотности потока отраженной волны к плотности потока падающей волны:

. (2.32)

Коэффициент прозрачности барьера определяется как отношение плотности потока волны, прошедшей через барьер, к плотности потока падающей волны:

. (2.32а)

Введенные коэффициенты удовлетворяют очевидному условию:

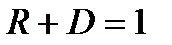. (2.33)