Диадические игры. Пример: экологический конфликт

Ранее был рассмотрен такой пример, при котором некоторое действие, совершаемое малым числом участников конфликта, доставляет этим участникам выгоды и при этом само по себе никому не причиняет ущерба; совершенное же одновременно большим числом участников конфликта, оно наносит вред всем, в том числе тем, кто его совершил. Именно такого типа оказываются многие вопросы природопользования. Действительно, если некоторый природный ресурс будет потребляться малым числом природопользователей, то вполне может быть, что эти природопользователи совершают экономически выгодные для себя действия, не представляющие опасности для данного природного ресурса (например, ввиду его регенерации) и таким образом для всех игроков, представляющих как бы общество в целом. Потребление этого ресурса большим числом природопользователей затрудняет восстановление ресурса и оказывается в конечном счете невыгодным для всех.

Недостаточно декларировать заповедность того или иного природного объекта. Необходимо подкреплять эту декларацию надлежащими мерами. Подобных мер может быть достаточно много, рассмотрим две из них. Первая носит как бы административный характер и состоит в следующем. Всем возможным потребителям природного ресурса предоставляется право безвозмездного, но ограниченного пользования. Желательно, чтобы эта мера была устойчивой, «самоконтролирующейся», т. е. чтобы ни один пользователь не превысил бы предоставленную ему квоту.

Другая мера (экономической природы) состоит в продаже билетов, дающих право неограниченного пользования ресурсом. Будем предполагать, что доход от продажи билетов будет обращаться на восполнение природного ресурса. Встает вопрос об обоснованных (справедливых) ценах на разные категории билетов.

Проанализируем две поставленные выше задачи, для простоты и единообразия рассмотрения сделаем их участниками знакомые нам предприятия.

Предприятия «Чайка», «Сокол» и «Утро» кроме разработки программных продуктов, осуществляют ведение побочного бизнеса.

Предположим, что для выпуска этой продукции предприятия забирают воду из некоторого водоема и в него спускают отработанную воду. Каждое из предприятий может работать по двум технологическим схемам. В соответствии с первой схемой отработанная вода оказывается загрязненной; безнаказанно ее можно сбрасывать в водоем лишь до некоторого предела, после чего вода в нем без предварительной обработки станет непригодной даже для нужд самих расположенных по берегам водоема предприятий, и расходы по этой технической обработке забираемой воды будут возрастать с ростом количества сбрасываемой загрязненной воды. В соответствии со второй схемой отработанная вода остается сравнительно чистой и может в любых количествах сбрасываться в водоем, не нарушая его экологического баланса.

Естественно предположить, что использование второй технологии обходится предприятию дороже, чем использование первой, однако склонность экономить на технологии в рассматриваемых условиях (т. е. склонность сбрасывать неочищенную воду) будет сдерживаться опасением, что такая «экономия» станет достаточно распространенным явлением и обернется потерями, которые превзойдут ее самое.

Определение 6.7. Бескоалиционная игра

Г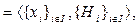

называется диадической, если каждый игрок в ней имеет две чистых стратегии 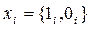для .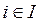

В диадической игре каждая смешанная стратегия 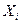игрока i полностью описывается вероятностью 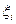выбора им своей первой чистой стратегии. Таким образом, множество 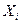всех смешанных стратегий игрока можно представить как сегмент [0,1], а множество всех ситуаций в смешанных стратегиях – как единичный n-мерный куб. Ситуации в чистых стратегиях будут соответствовать вершинам куба.

Всякая вершина куба ситуаций в диадической игре может быть задана как n-членная последовательность единиц и нулей. Для того чтобы её идентифицировать среди всех вершин, достаточно указать множество всех игроков, выбирающих в этой ситуации свою первую стратегию.

Диадическую игру трех лиц можно описать 3*2³=24 параметрами. Составим алгоритм решения такой игры.

Опишем множества 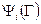для диадической игры трех лиц. Для определенности рассмотрим случай i=3, обозначив для краткости значения функции выигрыша 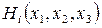этого игрока через .

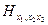Тогда можно записать [2]:

 

 

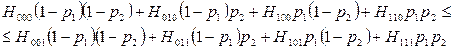
После преобразований получаем:

 

 

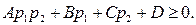
Граница описываемого данным неравенством множества в случае 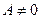есть гипербола. Построение этой гиперболы на единичном квадрате плоскости 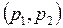приводит к описанию множества 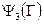и его геометрическому выражению. Аналогично строится каждое из множеств 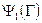и 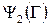. Пересечение

находится в результате геометрических рассуждений.

 

Рассмотрим пример.

Составим следующую игру.

Участники игры – игроки 1, 2 и 3 (рассматриваемые нами предприятия), располагающие двумя (первой и второй) стратегиями каждый. Таким образом, в конструируемой игре будет всего восемь ситуаций в чистых стратегиях. Введем в рассмотрение ситуации в смешанных стратегиях: тройки вида 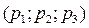, где каждое p_t, являющееся вероятностью выбора игроком t своей первой чистой стратегии, лежит между 0 и 1. Этим ситуациям можно поставить в однозначное соответствие точки единичного куба, причем вершины этого куба будут соответствовать ситуациям в чистых стратегиях.

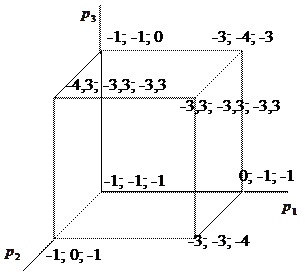
Рис. 6.2

 

При подсчете значений функций выигрыша игроков в игре будем исходить из следующих произвольных, но вполне правдоподобных допущений. Именно, будем считать, что использование каждым предприятием второй технологической схемы требует от него дополнительных затрат в 1 единицу по сравнению с применением первой. Использование первой технологии не более чем одним предприятием не порождает вовсе потерь от загрязнения воды.

 

Если первую технологию применяют предприятия 1 и 2 или 1 и 3, то потери от загрязнения воды для каждого ее пользователя составят 3 единицы, а если применяют 2 и 3 или, наконец, все три предприятия сразу, то 3,3 единицы.

 

Сделанные расчеты позволяют выписать значения функций выигрыша каждого из игроков в каждой из ситуаций. Например, если игроки 1 и 3 применяют свою первую чистую стратегию, а игрок 2 – вторую, то выигрыши игроков 1, 2 и 3 будут соответственно равны -3; -4; -3 (стоящие здесь минусы соответствуют тому, что выигрыши суть затраты, потери, взятые с обратным знаком). Так, подсчитанные тройки выигрышей на рис. 6.2 выписаны при всех вершинах куба ситуаций.

Интересующая нас игра полностью описана.

Будем искать в построенной игре ситуации равновесия. Они соответствуют возможным устойчивым договорам между нашими водопользователями, причем, как уже неоднократно отмечалось, устойчивость понимается здесь в том смысле, что ни один нарушитель договора не увеличит от нарушения своего выигрыша. Их можно, интерпретировать так же, как некоторые предписываемые надлежащей властью нормативы регионального водопользования; в этом случае устойчивость можно понимать как их соблюдение, даже при отсутствии контроля.

Итак, пусть 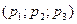‑ ситуация равновесия в смешанных стратегиях. Выпишем и проанализируем условия ее равновесности. Ограничимся анализом «приемлемости» этой ситуации для игрока 1 (остальные условия равновесности рассматриваются аналогично).

Ожидаемый выигрыш игрока 1 в ситуации 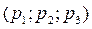подсчитывается по той же схеме, что и в случае игры из предыдущего раздела. Он равен:

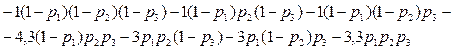
Мы ищем неизвестные р₁, р₂ и р₃ из условий неувеличения выигрыша (т. е. неуменьшения потерь) игрока 1 при замене им смешанной стратегии, соответствующей параметру p_it на какую-либо другую стратегию. В предыдущем примере оказалось достаточным выписать условия такого неувеличения при заменах p₁ только на 0 и на 1. Очевидно, что этого достаточно и в нашем примере. Здесь эти условия записываются в виде следующих неравенств:

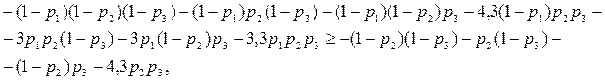
и

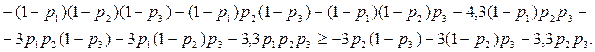
Преобразуем, как и в предыдущем разделе, эти неравенства к более удобному виду, перенеся в первом из них слева направо первые четыре члена:

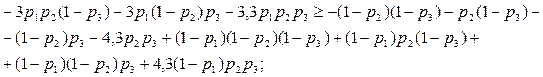
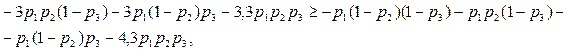
а во втором ‑ последние три:

 

 

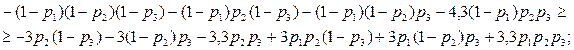
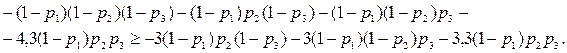
Приведение подобных членов даст нам:

 

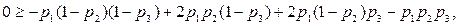(6.12)

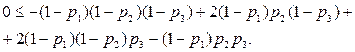(6.13)

 

Какие ситуации удовлетворяют этим неравенствам? Опишем отдельно те из Них, для которых 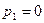, 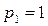и 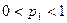. Если 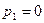, то неравенство (6.12) превращается в тождество, выполняющееся автоматически, и как условие может быть отброшено. Неравенство (6.13) превращается в

 

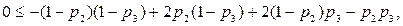(6.14)

 

или (после очевидных упрощений)

 

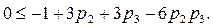(6.15)

 

Множество пар 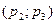, для которых 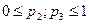и выполняется это неравенство, составляет заштрихованную часть единичного квадрата, лежащую между двумя дугами гиперболы, изображенного на рис. 6.3, включая сами эти дуги.

Рис. 6.3

 

Если 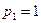, то тождественным оказывается неравенство (6.13), а (6.12) после упрощений имеет вид:

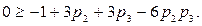(6.16)

Множество таких пар на рис.6.3 описывается двумя незаштрихованными кусками квадрата вместе с их границами.

Наконец, если 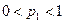, то оба неравенства (6.12) и (6.13) поддаются сокращению на р₁ и соответственно на 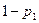, что дает нам одновременно оба неравенства (6.15) и (6.16), т. е. равенство

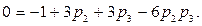(6.17)

Следовательно при любом р₁, расположенном строго между 0 и 1, геометрическое место точек 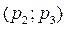, удовлетворяющих нашему условию, есть пара дуг гиперболы.

Похожие множества составляют и ситуации, от которых невыгодно отклоняться игроку 2 (и соответственно игроку 3).

Первое из них представляет собой кусок цилиндрической поверхности, описываемой уравнением

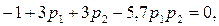(6.18)

дополненной соответствующими кусками горизонтальных граней куба ситуаций, а второе ‑ куском цилиндрической поверхности, описываемой уравнением

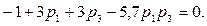(6.19)

и опять-таки с соответствующими плоскими дополнениями.

Общая часть всех этих описанных множеств имеет только одну точку, лежащую на поверхности куба: ситуацию (1,1,1).

Остальные ситуации равновесия лежат строго внутри куба₁ ситуаций. Для них 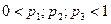, и потому они должны лежать на пересечении всех трех гиперболических цилиндров с уравнениями (6.17), (6.18) и (6.19). Следовательно, для нахождения этих точек необходимо решить систему уравнений (6.17), (6.18) и (6.19).

Делается это достаточно просто, тем более что в уравнения(6.18) и (6.19) неизвестные р₂ и р₃ входят относительно р₁ одинаковым образом и находятся по р₁ однозначно. Следовательно, при каждом значении p₁ из какого-либо решения системы в этом решении должно быть 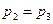. В связи с этим полагая в уравнении (6.17) 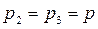, получаем 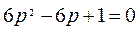, откуда:

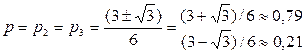
Далее, из уравнения (6.16) находим 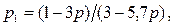(6.20)

так что 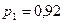и .

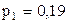Таким образом, дополнительно к найденной ситуации равновесия (6.20) мы получаем еще вторую и третью ситуации равновесия

(0,92; 0,79; 0,79), (0,19; 0,21; 0,21) (6.21)

Каждая из трех найденных ситуаций равновесия отражает некоторое возможное психологическое отношение ко всей проблеме со стороны ее участников и органа, регулирующего природопользование.

Ситуация (1, 1, 1), допускающая неограниченное загрязнение воды всеми предприятиями, соответствует отсутствию какого-либо внешнего регулирования вопроса, при котором участники ищут себе оправдания в формуле: «А что мне остается делать?»

Ситуация (6.21) соответствует весьма мягкому варианту правил водопользования и так же допускает значительное загрязнение водоема. Положительная ее роль состоит в том, что предприятия вынуждены действовать, учитывая в некоторой степени последствия от своих действий, и понимать, что увеличение вероятности загрязнения воды бьет, прежде всего, (подчеркнем еще раз, что именно в этом суть ситуации равновесия!) по собственным интересам. Заметим, что мягкие правила дозволяют применять загрязняющую технологию с вероятностью 92 %.

Другая ситуация отвечает, напротив, довольно жесткому варианту правил: загрязнение запрещается, если его вероятность превосходит 1/5 . И в этом случае ни один из водопользователей не заинтересован в нарушении правил. Первым загрязняющая технология разрешается с вероятностью 19 %, а вторым ‑ с вероятностью 21 %.