Задачи по курсу «Физические основы фотоники» и их решения

1. (Г.3) Вычислить градиент функции , зависящей только от модуля радиус-вектора .

Решение

Ответ

2. (Г.5) Вычислить, , , , , , где – постоянный вектор.

Решение

1)

 

2)

3)

4)

5)

Ответ

3. (Г.8) Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

если объем, который охватывает замкнутая поверхность, равен ; – постоянный вектор.

Решение

Теорема Гаусса-Остроградского:

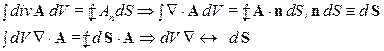
1)

 

 

2)

3) *

a.

 

b.

 

i.

Если область интегрирования имеет центр симметрии, то

ii.

Ответ

4. (Г.12) Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара. Объемная плотность заряда равна , радиус шара .

Решение

1)

2)

Ответ

Объединяя 1 и 2, получим:

5. (Г.13) В равномерно заряженном шаре с объемной плотностью заряда имеется шарообразная полость, центр которой расположен на расстоянии от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно и .

Решение

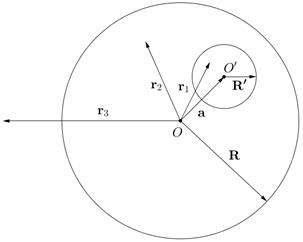
Поле в случае шара с полостью находится как сумма (суперпозиция) двух полей: поля сплошного шара радиуса с плотностью и шара радиуса с центром в точке и с плотностью , при этом – координаты точек наблюдения относительно . В расчетах используются результаты задачи 4.

Ответ

Объединяя три решения, запишем:

6. (Г.30) Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

Решение

Ответ

7. (А.52, Г.32) Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону: .

Решение

Ответ

8. (Г.50) Определить потенциал точечного заряда , находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

Решение

В главных осях:

Уравнение Пуассона

Ответ

9. (А.190')Внутри бесконечного цилиндра радиуса параллельно его оси течет однородный ток с объемной плотностью . Пользуясь интегральной формой уравнения Максвелла , найти напряженность магнитного поля внутри и снаружи цилиндра.

Решение

1)

2)

Ответ

 

10. (Г.65) Найти напряженность магнитного поля внутри и вне цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью . Оси цилиндра, образующего полость, и цилиндрического проводника, параллельны и находятся друг от друга на расстоянии .

Решение

– поле, создаваемое сплошным цилиндром по формулам задачи №42.

– поле, создаваемое сплошным цилиндром радиуса , ось которого удалена от на вектор и по которому течет ток .

1)

2)

 

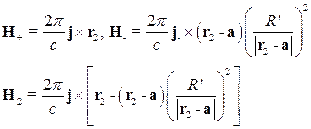
3)

Ответ

11. (Г.81) Показать, что постоянное однородное магнитное поле можно описывать векторным потенциалом .

Решение

12. (Г.140) Найти интенсивность излучения частицы массы , движущейся по круговой орбите радиуса , под действием кулоновских сил. Выразить ответ через энергию частицы.

Решение

Интенсивность дипольного излучения:

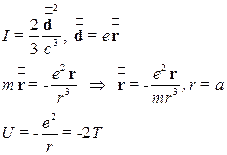
Из теоремы о вириале (см. ЛЛ. Т.1, §10):

Ответ

 

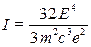
13. (А.9) Определить напряженность и потенциал электростатического поля равномерно заряженного шара радиуса . Суммарный заряд шара .

Решение

Ответ

14. (А.40) Вычислить энергию электростатического поля равномерно заряженного шара радиуса .

Решение

1 способ

2 способ

Ответ

 

15. (Г.56) Средняя плотность электронного облака в атоме водорода описывается функцией где боровский радиус, а расстояние до протона, имеющего заряд . Чему равна электростатическая энергия взаимодействия протона с электронным облаком.

Решение

Ответ

16.Вычислить дипольный момент равномерно заряженного полушара радиуса R, суммарный заряд полушара Q. Отрицательный заряд – Q помещен на расстояние l от центра по оси симметрии.

Решение

Ответ

17.Определить дипольный и квадрупольный моменты системы, смещенной относительно начала координат на вектор .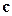

Решение

вектор трансляции, точка, в которой рассчитывается момент, .

1) Дипольный момент:

где дипольный момент системы, помещенной в начало координат.

2) Квадрупольный момент:

где, квадрупольный момент системы, помещенной в начало координат.

Ответ

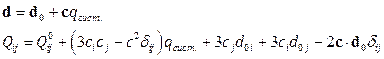
18.Внутри шара радиуса а задан вектор плотности тока . Найти распределение векторного потенциала внутри и снаружи шара.

Решение

1 способ

,

Соответственно ненулевой компонентой будет только .

Рассмотрим область снаружи шара :

Рассмотрим область внутри шара :

Заметим, что и Окончательно получаем:

2 способ

Ответ

19. (А.89) Выразить через - функцию распределение объемной плотности точечного диполя с моментом , находящегося в точке с радиус вектором .

Решение

Точечный заряд:

Точечный диполь:

Точечная плотность тока:

 

Нестационарная поляризация:

20. (А.246) Заряд е совершает гармонические колебания вдоль оси Х по закону . Написать выражение для объемной плотности заряда и объемной плотности тока . Найти средние по времени за период объемные плотности заряда и тока .

Решение

По определению: и .

Следовательно:

Найдем средние значения, как и .

Используем свойство - функции: где - нули функции .

Интервалу от 0 до Т из всего множества корней принадлежат только 2:

Возвращаясь к интегралу, получим:

Это выражение справедливо при , т.к. в случае интеграл даст 0.
Аналогично показывается, что: .

Ответ

21. (А.258) Радиус – вектор точки расположения диполя с моментом меняется по закону . Определить распределение объемных плотностей заряда и тока в пространстве. Вычислить магнитный момент найденного тока.

Решение

То есть .

Ответ

22.Радиус – вектор точки расположения диполя с моментом меняется по закону . Определить потенциалы и , напряженности электрического и магнитного полей, плотность тока и квадрупольный момент.

Решение

 

 

23. (А.292) Простейшая линейная антенна представляет собой тонкий прямолинейный провод длины l, по которому течет ток . Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока.

Решение

Пусть проводник соединяет две сферы. Заряд каждой сферы . В этом случает ток . Таким образом, в целом, система представляет собой простейший диполь: . В результате интенсивность излучения такой системы равна:

Интенсивность усредненная, за период колебаний тока , равна:

Ответ

24. (А.298) Протон с массой m и зарядом е движется перпендикулярно однородному постоянному магнитному полю с напряженностью . Его кинетическая энергия в начальный момент времени равнялась . Найти закон убывания кинетической энергии , обусловленный дипольным излучением.

Решение

Уравнение движения:

Т.к. направление поля перпендикулярно движению заряда, то .
Тогда

Интенсивность излучения - это энергия электромагнитного поля, излучаемая в единицу времени, т.е.

Решая это дифференциальное уравнение, находим закон убывания кинетической энергии:

Ответ

25. (А.300)В классической модели атома, предложенной Резерфордом, электрон с зарядом е и массой m вращается по круговой орбите вокруг неподвижного ядра с зарядом . Найти закон убывания полной энергии электрона, обусловленный дипольным излучением. Вычислить время , по истечению которого электрон упадет на ядро вследствие потери энергии на дипольное излучение. В начальный момент времени электрон находился на расстоянии R от ядра.

Решение

Выразим интенсивность дипольного излучения через полную энергию электрона. Воспользуемся теоремой о вириале: если частица движется в потенциальном поле с энергией , то кинетическая энергия . В данном случае потенциальная энергия электрона в поле ядра , то

Следовательно, уравнение движения:

Решая дифференциальное уравнение, находим:

Где .

При падении частицы на центр , т.к. . Таким образом:

.

Ответ

26. (А.302) Доказать, что у замкнутой системы заряженных частиц с одинаковым отношением заряда к массе дипольное излучение отсутствует.

Решение

1 способ

Интенсивность дипольного излучения: .

Закон движения: .

Дипольный момент системы точечных зарядов: .

Таким образом: .

Поскольку система замкнутая, то векторная сумма внешних сил равна 0. Следовательно .

2 способ

 

27. (А.324) Замкнутая система состоит из конечного числа частиц с одинаковым отношением заряда к массе. Доказать, что магнитно-дипольное излучение у такой системы отсутствует.

Решение

 

28. (А.313) Простейшая рамочная антенна представляет собой прямоугольную рамку со сторонами а и b, по которым течет ток . Определить интенсивность I длинноволнового излучения антенны в среднем за период колебаний тока.

Решение

По определению магнитный момент линейного тока: .
Т.к. , то , где площадь сечения S=ab, следовательно:

Отсюда интенсивность магнитно – дипольного излучения такой антенны равна:

Интенсивность, усредненная за период колебаний:

Ответ

 

29. (А.315)При каком условии интенсивность магнитно – дипольного излучения не зависит от выбора начала координат?

Решение

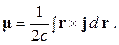
Если система транслирована относительно начала координат на вектор , то заменяем и для магнитного момента имеем:

где - магнитный момент системы в начале координат.
Воспользуемся соотношением: , где индекс 0 означает, что дипольный момент рассчитан в начале координат.
Интенсивность магнитно – дипольного взаимодействия: .

Таким образом, для того, чтобы интенсивность не зависела от выбора начала координат необходимо, чтобы выполнялось равенство . Это реализуется в случае .

Ответ

30. (А.329) При каком условии интенсивность квадрупольного излучения не зависит от выбора начала координат?

Решение

Квадрупольный момент системы, транслированный на вектор (см. задачу 16):

где дипольный момент системы, помещенной в начало координат.

Интенсивность квадрупольного излучения: .

Таким образом, для того, чтобы интенсивность квадрупольного излучения не зависела от выбора начала координат необходимо, чтобы выполнялось равенство . Это реализуется в случае и .

Ответ

31.Вычислить интеграл:

.

Решение

Ответ

32.Вычислить интеграл:

.

Решение

Ответ

33. (А.10а, Б.77) Поверхность равномерно заряжена с поверхностной плотностью . Найти напряженность и потенциал электрического поля в каждой точке пространства, если заряженная поверхность имеет форму сферы радиусом R.

Решение

Ответ

34. (Б.81)Заряд распределен сферически симметричным образом: . Разбив распределение заряда на сферические слои, выразить через потенциал и напряженность поля (записать и в виде однократного интеграла по ).

Решение

Ответ

 

35. (Б.81)Заряд распределен сферически симметричным образом: . Разбив распределение заряда на сферические слои, выразить через потенциал и напряженность поля (записать и в виде однократного интеграла по ), где:

.

Решение

Ответ

36. (А.11) Шар радиуса заряжен сферически-симметрично с объемной плотностью , где – постоянная. Чему равен поток напряженности электрического поля через круг радиуса , плоскость которого в центральной точке касается шара?

Решение

1 способ

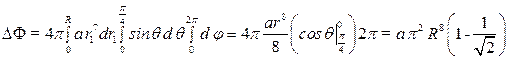
2 способ

Ответ

37. (А.12)Средняя плотность заряда электронного облака в атоме водорода равна , где а – боровский радиус, а r – расстояние до протона, имеющего заряд е. Определить напряженность электрического поля в атоме водорода. Исследовать на малых и больших расстояниях от протона.

Решение

Ответ

 

38. (А.44) Средняя плотность заряда электронного облака в атоме водорода равна , где а – боровский радиус, а r – расстояние до протона, имеющего заряд е. Учитывая вклады от протона и электронного облака, найти распределение потенциала электрического поля внутри атома. Исследовать на малых и больших расстояниях от протона. Чему равна электростатическая энергия взаимодействия U , а также собственная электростатическая энергия W электронного облака.

Решение

Ответ

39. (Б.127) Диполь с моментом находится в начале координат, а другой диполь с моментом в точке с радиус – вектором . Найти энергию взаимодействия U этих диполей и действующую между ними силу F. При какой ориентации диполей эта сила максимальна.

Решение

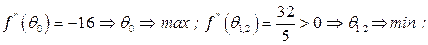
40. (А.19) Напряженность электрического поля в пространстве известна:

где и – положительные постоянные, а – расстояние до начала координат. Определить распределение объемной плотности заряда, создавшего это поле. Чему равен полный заряд ?

Решение

Ответ

41. (Г.10)Показать, что дивергенция вектора

равна нулю.

Решение

Ответ

42. (Г.31) Найти дифференциальное уравнение, которому удовлетворяет потенциал

.

Решение

43.Найти потенциала .

Решение

Ответ