ТЕМА 3. ПРИМЕНЕНИЕ МЕТОДОВ ФИНАНСОВОЙ МАТЕМАТИКИ В РЕШЕНИИ ТИПОВЫХ АНАЛИТИЧЕСКИХ ЗАДАЧ

Современная рыночная экономика предполагает использование различных финансовых инструментов предпринимательства. В роли этих инструментов в настоящее время выступают банковская система страны, пакеты ценных бумаг и котировки валют, пенсионная и страховая системы, капитальные вложения в инвестиционные проекты и т.д. Все эти экономические элементы объединяет необходимость оценивания эффективности использования финансовых ресурсов.

Такие финансовые сделки представляют собой особую группу экономических процессов, касающихся изменения стоимости денег во времени. Их сущность заключается в том, что стоимость суммы денег, зафиксированная в определенный момент с течением времени не остается постоянной. Это происходит под действием инфляционных процессов, а также при вовлечении денежных средств в товарный или производственный оборот. В результате тех или иных действий их реальная стоимость с течением времени может уменьшаться либо увеличиваться.

В наиболее общем виде финансовые сделки можно представить упрощенно следующим образом. Из двух участников сделки – первый (кредитор) обладает необходимой суммой денежных средств, которая нужна другому (берущему в долг) для осуществления собственных планов. Кредитор отдает эти средства с расчетом получения дохода от их одалживания и возврата выданных денег через определенное время, согласованное в договорном порядке. При этом обговариваются условия сделки: первоначальная сумма денег, размер предполагаемого дохода кредитора и сроки реализации финансовой сделки.

Расчеты эффективности финансовых операций, связанных с изменением стоимости денег, проводятся с помощью приемов финансовой математики. Основой расчетов являются методы наращения денежной стоимости или ее удержания (дисконтирования).

Наиболее простым методом финансовых вычислений является расчет наращенной стоимости денег с помощью процентной ставки.

Различают два вида расчета процентной ставки: простые проценты и сложные проценты.

Метод простых процентов заключается в присоединении к начальной сумме денег полученного за период n дохода, представляющего определенную процентную долю от начальной суммы:

,

где конечная (наращенная) сумма денег, полученная через время (t);

- начальная сумма вложенных денег;

- доход от использования начальной суммы денег;

- процентная ставка дохода от начальной суммы денег.

Пример. Необходимо определить наращенную сумму денег за 2 года, если начальная сумма вложенных средств составила 300 тысяч рублей, а ставка простых процентов – 15% годовых.

рублей.

Из формулы простых процентов при необходимости можно рассчитать значение начальной суммы вложений, процентную ставку и период начисления.

; ; .

На практике бывает, что ссуда выдается на неполный финансовый год. В этом случае процентная ставка умножается не на цельный период начисления, а на его дробную часть. Формулу простого процента можно представить следующим образом:

, где , t – число дней (месяцев) ссуды, k – число дней (месяцев) в году.

Пример. Необходимо вычислить наращенную сумму денег за 8 месяцев при ставке процентов - 15% годовых, если начальный вклад составил 200 тысяч рублей.

тыс. рублей.

При долгосрочных финансово-кредитных операциях более выгодным является начисление дохода по методу сложных процентов. Суть его заключается в том, что если начисленные проценты за определенный период не востребованы, то они присоединяются к первоначальному вкладу, образуя большую стоимость его, и уже в следующем периоде проценты начисляются на увеличившуюся сумму денег. Процесс присоединения процентного дохода к начальной сумме называется реинвестированием или капитализацией процентов.

Расчет по формуле сложных процентов выглядит следующим образом:

;

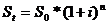Величину называют множителем наращения сложных процентов.

Значения этого множителя для целых чисел n приводятся в таблицах сложных процентов для n, равных от 1 до 50, 60, 70, 80, 90, 100 лет.

Пример. Необходимо определить по таблице 5.1 значение суммы будущего долга через 15 лет, если начальная сумма составляет 200 тыс. рублей, а годовая процентная ставка – 10%.

тыс. рублей.

1 время (t)

Схемы развития наращенных сумм по простым и сложным процентам отличаются разной эффективностью отдачи для кредиторов, например, для банков. При выдаче кредита сроком до одного года банку выгоднее использовать формулу простых процентов, которая дает больший доход по сравнению со сложными процентами. При выдаче кредита сроком более года выгоднее использовать формулу сложных процентов. При этом, чем больше временной период, тем больше эта разница.

Бывают ситуации, когда необходимо представить эффективность наращивания по формуле сложных процентов в более понятном виде простых процентов. Этот процесс, называющийся определением эквивалентной ставки, выглядит следующим образом:

, где - ставка сложных процентов; - ставка простых процентов.

; .

Пример. На депозитный вклад положено 200 тыс. руб. на срок 3 года под 15 % годовых, рассчитываемых по схеме сложных процентов. Определить годовую ставку простых процентов, при которой будет получен такой же результат.

или 17,3625%

тыс. руб.

тыс. руб.

На практике часто случается, что ставка сложных процентов начисляется несколько раз в году (поквартально, помесячно, ежедневно и т.д.). В этом случае необходимо учитывать частоту начисления сложных процентов по формуле:

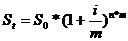, где m частота начисления процентов в году.

Пример. Необходимо сравнить наращенную сумму при двух вариантах по формуле сложных процентов, если начисление 15% годовых на протяжении 5 лет производится: 1) ежемесячно и 2) ежеквартально. Начальная сумма составляет 200 тыс. руб.

1) тыс. рублей.

2) тыс. рублей.

Таким образом, при первом варианте наращенная сумма получилась больше, чем во втором варианте. Чем чаще идет начисление сложных процентов, тем большим будет полученный результат.

При таком способе начисления процентов в финансовых документах могут указывать величину эффективной ставки, которая показывает процентную ставку, дающую тот же результат, что и m – разовое начисление в год. Эффективная ставка ( ) находится из следующего соотношения:

, где n = 1

.

Пример. Определить эффективную ставку, если номинальная годовая ставка при помесячном начислении равна 25%:

Таким образом, применяя годовую ставку простых процентов 28,073%, будет получен тот же результат, что и при начислении помесячно 25%.

Реальные экономические условия связаны с необходимостью учета влияния инфляционных процессов при совершении финансовых операций.

Инфляция проявляется в увеличении цен и снижении покупательной способности денег. Поэтому с помощью методов финансовой математики можно узнать реальную стоимость наращенного капитала с учетом инфляции. Логика такого вычисления заключается в следующем:

1) определение индекса цен ( ) , который является отношением средней величины цен в отчетном периоде ( ) к средней величине цен в базисном периоде ( ): ;

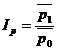2) расчет индекса покупательной способности денег ( ), который является обратным величине индекса цен: ;

3) расчет реальной наращенной суммы денег (с учетом инфляции):

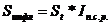
Если наращение производится по простой ставке, реальная наращенная сумма равна:

;

При наращении по сложным процентам реальная наращенная стоимость будет:

;

Пример. Определить реальную наращенную стоимость вложений через 4 года, если на депозит положено 100 тыс. рублей под 12% годовых, рассчитываемых по схеме сложных процентов. По прогнозу на 4 года индекс цен (инфляции) составит 1,45:

тыс. рублей

В данном примере вложенные средства не обесценились, их реальная стоимость увеличилась, то есть процентная ставка превышала уровень инфляции.

Если необходимо определить реальную наращенную стоимость денег за несколько месяцев и известны ежемесячные темпы инфляции, то можно использовать такую формулу:

,

где m – частота начисления процентов в течение года;

t- число месяцев;

h – ожидаемый месячный темп инфляции.

Пример. Определить реальную наращенную стоимость через 6 месяцев, положенных на депозит 500 тыс. рублей под 15 % годовых, которые начисляются ежемесячно. Ежемесячный темп инфляции прогнозируется в размере 1,5%.

тыс. рублей.

Эрозия (обесценивание) капитала составит: 492,656 – 500,000=-7,344 тыс. рублей.

Дисконтирование позволяет расчитать величину снижения стоимости денег по известной ставке дисконта. Действие дисконтирования является обратным определению наращения процентов: нужно определить какая процентная доля вычитается (удерживается) за определенное время из начальной суммы. В банках процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом.

Стоимость одной суммы денег сейчас и в будущем не является одинаковой, через некоторое время на эту сумму уже можно будет купить меньше товаров. При помощи математического дисконта можно определить реальную (на момент их оценивания) стоимость денежных средств полученных в будущем. Расчет дисконтированной стоимости производится по следующей формуле:

,

где - реальная (дисконтированная) стоимость денег через n лет; - дисконтирующий множитель, который показывает, во сколько раз уменьшится первоначальная стоимость 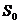, при ставке d процентов годовых к концу n-го года. В финансовых вычислениях за ставку дисконта можно принять темп инфляции.

Пример. Нужно определить величину вложений на банковский депозит сегодня, чтобы получить через 3 года под 8% годовых доход в размере 150 тыс. руб.:

тыс. рублей.

Несколько иным по способу расчета дисконтируемой величины является банковский (коммерческий) учет, который использует учетную ставку, тогда как математический дисконт использует ставку наращения.

Учетная ставка используется при определении стоимости векселя для учета его банком. Обычно банк покупает вексель до наступления срока платежа по нему по цене, которая меньше указанной на векселе. При наступлении срока платежа банк реализует вексель по номинальной стоимости, а разница (дисконт) с ценой, в которую он обошелся банку при покупке, составит доход. Владелец векселя выигрывает на том, что получает деньги раньше срока, хотя и в меньшем размере.

Расчет суммы, выплачиваемой при учете векселя, будет производиться по следующей формуле:

, где d учетная ставка (дисконт).

Пример. Владелец векселя суммой 100 тыс. руб. со сроком погашения через 40 дней, решил получить деньги на 20 дней раньше при условии, что банк учтет вексель под 25% годовых. Какую сумму получит векселедержатель?

тыс. рублей.

В этом примере банк получил выгоду в размере удержанного дисконта, 100 – 98,611= 1,389 тыс. рублей.

Простая учетная ставка (дисконт) иногда применяется и при расчете наращенной суммы. В частности, если возникает необходимость оплатить ссуду в самом начале срока ее получения. Для банка выдавать кредит под простую учетную ставку более выгодно, чем под простые проценты. Формула расчета выглядит следующим образом:

.

Пример. Определить наращенную сумму с помощи учетной ставки 15% годовых, если начальная сумма равняется 200 тыс. рублей и выдана на 2 года. Сравнить с начислением по схеме простых процентов.

а) тыс. рублей.

б) 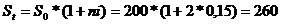тыс. рублей.

Как видно из расчетов, начисление по простому дисконту оказалось выгоднее на 25,714 тыс. рублей.

Расчет дисконтированной суммы денег является важным финансовым инструментом для принятия решения об инвестировании средств. В этом случае инвестору нужно узнать какую реальную стоимость составят его доходы от инвестиций через несколько лет, и принять решение о целесообразности вложений. Сумма дисконтированных доходов определяется по формуле:

,

где - общая накопленная величина дисконтированных доходов;

- величина дохода за n-й год.

Пример. Определить общую накопленную величину дисконтированных доходов за 3 года реализации инвестиционного проекта, если в течение этих лет ежегодный доход составит 100 тыс. рублей. Средняя ставка дисконта предположительно составит 15%:

тыс. рублей.

Следовательно, сейчас реальная стоимость накопленного через 3 года дохода составит не 300 тыс. рублей, а 228,323 тыс. рублей. Если инвестор в проект вложит сумму больше реальной стоимости, то заниматься этим проектом не целесообразно.