Тепловые двигатели и холодильные машины. Цикл Карно и его к. п. д. для идеального газа

Из формулировки второго начала термо­динамики по Кельвину следует, что вечный двигатель второго рода— периодически действующий двигатель, совершающий работу за счет охлаждения одного источ­ника теплоты,— невозможен. Для ил­люстрации этого положения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигате­лей) .

Принцип действия теплового двигате­ля приведен на рис. 85. От термостата с более высокой температурой Т₁, называ­емогонагревателем,за цикл отнимается количество теплоты Q₁, а термостату с бо­лее низкой температурой T₂, называемомухолодильником,за цикл передается коли­чество теплоты Q₂, при этом совершается работа A = Q₁-Q₂.

Процесс, обратный происходящему в тепловом двигателе, используется в хо­лодильной машине, принцип действия ко­торой представлен на рис. 86. Системой за цикл от термостата с более низкой темпе­ратурой T₂ отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой Т₁количество теплоты Q₁. Для кругового процесса, согласно (56.1), Q=A, но, по условию, Q=Q₂-Q₁<0, поэтому A<0 и Q₂-Q₁=-A, или Q₁=Q₂+A, т. е. количество теплоты Q₁, от­данное системой источнику теплоты при более высокой температуре Т₁, больше количества теплоты Q₂, полученного от источника теплоты при более низкой тем­пературе Т₂, на величину работы, совер­шенной над системой. Следовательно, без совершения работы нельзя отбирать теп­лоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинами­ки в формулировке Клаузиуса.

18.При рассмотрении реальных газов — газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях £ 10–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.Основу межмолекулярного взаимодействия составляют кулоновские силы взаимод. между электронами и ядрами одной молекулы и ядрами и электронами другой.Уравнение Ван-дер-Ваальса примет вид

где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).

Изотермы Ван-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые имеют довольно своеобразный характер. При высоких температурах (T > Tк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Tк на изотерме имеется лишь одна точка перегиба К.Эта изотерма называется критической.

19.Жидкостиàтела, характеризующиеся, как и газы, способностью "течь" (см. Вязкость), особой подвижностью частиц и в то же время обладающие определенным, ограниченным собственной поверхностью тела объемом.Дальний порядок и ближний порядок (далее Д) упорядоченность во взаимном расположении или молекул в твердых телах и жидкостях. Упорядоченность на расстояниях, сравнимых с межатомными, называется ближним порядком, а упорядоченность, повторяющаяся на неограниченно больших расстояниях, - дальним порядком. В идеальном газе расположение в какой-либо точке пространства не зависит от расположения других.Смачивание — это поверхностное явление, заключающееся во взаимодействии жидкости с поверхностью твёрдого тела или другой жидкостью при условии, что присутствует третья (обычно, но не обязательно, газовая) фаза, причём происходит одновременный контакт всех этих трёх не смешивающихся фаз. Смачивание ответственно за растекание жидкости по твёрдой поверхности, за форму лежащих на ней капель, за пропитывание порошков и пористых веществ (капиллярные явления) и др. Капиллярные явления - физические явления, обусловленные действием поверхностного натяжения на границе раздела несмешивающихся сред. К капиллярным явлениям относят обычно явления в жидких средах, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собственным паром. Искривление поверхности ведёт к появлению в жидкости дополнительного капиллярного давления Dp, величина которого связана со средней кривизной r поверхности уравнением Лапласа: Dp = p1 — p2 = 2s12/r, где (s12 — поверхностное натяжение на границе двух сред; p1 и p2 — давления в жидкости 1 и контактирующей с ней среде (фазе) 2. В случае вогнутой поверхности жидкости (r < 0) давление в ней понижено по сравнению с давлением в соседней фазе: p1 < p2 и Dp < 0. Для выпуклых поверхностей (r > 0) знак Dp меняется на обратный. Капиллярное давление создаётся силами поверхностного натяжения, действующими по касательной к поверхности раздела.

20. Предмет классической электродинамики

Раздел физики, в котором исследуются свойства электромагнитного поля и взаимодействующих с ним других видов материи, называют классической электродинамикой.

Электромагнитное поле представляет собой самостоятельный вид материи. Словосочетание «электромагнитное поле» характеризует его особый вид материи. Электрическое поле, как и всякий физический объект, характеризуется состоянием и уравнениями движения. В каждый момент времени состояние электромагнитного поля описывается двумя полями: электрическим и магнитным. Уравнения движения для электромагнитного поля содержатся в микроскопических уравнениях Максвелла. Микроскопические уравнения Максвелла совместно с уравнениями Лоренца для заряженных частиц образуют фундаментальную систему уравнений классической электродинамики. Наряду с микроскопическими, используются макроскопические уравнения Максвелла, макроскопические уравнения Лоренца и материальные уравнения (например, закон Ома), которые образуют макроскопическую систему уравнений. При электризации тел выполняется закон сохранения электрического заряда. Этот закон справедлив для замкнутой системы. В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. Если заряды частиц обозначить через q1, q2 и т.д., то

q1 + q2 + q3 + … + qn = const.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними. Эту силу называют кулоновской. , где

|q1| и |q2| - модули зарядов тел,r– расстояние между ними, k – коэффициент пропорциональности.F- сила взаимодействия

Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела.

Напряженность электрического поля.

Отношение силы, действующей на помещенный в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля.

Напряженность поля равна отношению силы, с которой поле действует на точечный заряд, к этому заряду.

Напряженность поля точечного заряда. .

Модуль напряженности поля точечного заряда qo на расстоянии r от него равен: .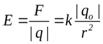

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых 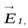и т. д., то результирующая напряженность поля в этой точке равна:

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленнойна : .

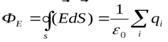Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностьюSпроизвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS, к каждой из которыхпроведем вектор нормали .

Элементарный поток вектора напряженности через площадкуdS(рис. 2.8) определится соотношением: ,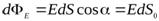

где –проекция на направление нормали 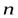. Тогда , где - элементарный телесный угол, под которым элемент виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьSот точечного зарядаq, находящегося внутри этой поверхности.

,

так как , то .

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS1иdS2, находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда 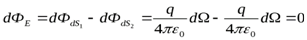, следовательно, поток напряженности электрического поля через любую поверхностьS, не охватывающую заряды равен нулю, т.е.ФЕ=0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на : (1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то теорема Гаусса имеет вид (2)

где интеграл справа берется по объему V, охватываемому поверхностьюS.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле зависит от конфигурации всех зарядов, поток сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS. Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности, то изменится всюду, и на поверхностиS, апоток вектора через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

При электризации тел выполняется закон сохранения электрического заряда. Этот закон справедлив для замкнутой системы. В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. Если заряды частиц обозначить через q1, q2 и т.д., то

q1 + q2 + q3 + … + qn = const.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними. Эту силу называют кулоновской. , где

|q1| и |q2| - модули зарядов тел,

r – расстояние между ними,

k – коэффициент пропорциональности.

F- сила взаимодействия

Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела.

Напряженность электрического поля.

Отношение силы, действующей на помещенный в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля.

Напряженность поля равна отношению силы, с которой поле действует на точечный заряд, к этому заряду.

Напряженность поля точечного заряда. .

Модуль напряженности поля точечного заряда qo на расстоянии r от него равен: .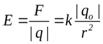

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых 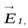и т. д., то результирующая напряженность поля в этой точке равна:

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленнойна : .

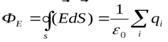Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностьюSпроизвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS, к каждой из которыхпроведем вектор нормали .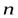

Элементарный поток вектора напряженности через площадкуdS(рис. 2.8) определится соотношением: ,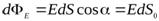

где –проекция на направление нормали 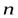. Тогда , где - элементарный телесный угол, под которым элемент виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьSот точечного зарядаq, находящегося внутри этой поверхности.

,

так как , то .

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS1иdS2, находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда 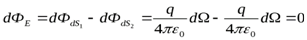, следовательно, поток напряженности электрического поля через любую поверхностьS, не охватывающую заряды равен нулю, т.е.ФЕ=0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на : (1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то теорема Гаусса имеет вид (2)

где интеграл справа берется по объему V, охватываемому поверхностьюS.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле зависит от конфигурации всех зарядов, поток сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS. Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности, то изменится всюду, и на поверхностиS, апоток вектора через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.