 |
Главная |
Практическая работа №2
|
из
5.00
|
2.1 Пирамида:
Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.
наклонная прямая

Элементы пирамиды

апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины [ℓ];
боковые грани — треугольники, сходящиеся в вершине пирамиды;
боковые ребра — общие стороны боковых граней;
вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра) (Н);
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
основание — многоугольник, которому не принадлежит вершина пирамиды.
Правильная пирамида

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
боковые ребра правильной пирамиды равны; в правильной пирамиде все боковые грани — равные равнобедренные треугольники; в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
Прямоугольная пирамида

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Самостоятельная работа
1. В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 10, BD= 48. Найдите боковое ребро SA.
2. В правильной четырехугольной пирамиде сторона основания равна 5 см, а высота 7 см. Найдите площадь поверхности пирамиды.
3. В правильной треугольной пирамиде SABC точка R - середина ребра BC, S – вершина. Известно, что АВ = 7, а SR = 16. Найдите площадь боковой поверхности пирамиды.
4. Сторона основания правильной шестиугольной пирамиды равна 4 см, а угол между боковой гранью и основанием равен 45˚. Найдите площадь боковой поверхности пирамиды. В ответе укажите S/  .
.
5. В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 45°. Расстояние от центра основания до боковой грани равно √6 см. Найдите площадь боковой поверхности пирамиды.
Усечённая пирамида

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Боковая поверхность — это сумма площадей боковых граней.
Для нахождения боковой поверхности в правильной пирамиде можно использовать формулу: Sб.п.= 1/2•Р•ℓ
Полная поверхность — это сумма площади боковой поверхности и площади основания.
Для нахождения полной поверхности в правильной пирамиде можно использовать формулу: Sп.п. = 1/2•Р•ℓ+Sосн.
Объем пирамиды (любой) может быть вычислен по формул: V = 1/3•Sосн.•Н
Сечения пирамиды:



диагональное сечение плоскостью параллельной сечение плоскостью
под углом к основанию
Пример: Найти площадь боковой, полной поверхности, объем пирамиды.
Ход работы
А) Для нахождения площади боковой поверхности пирамиды нужно измерить линейкой следующие элементы: апофему, стороны основания, высоту. Подставить значения в формулу для нахождения пощади (если пирамида правильная). Если пирамида наклонная, то боковую поверхность находим из суммы площадей граней.
Б) Для нахождения площади полной поверхности пирамиды нужно найти площадь основания пирамиды (площадь треугольника, прямоугольника, ромба)
В) Площадь полной поверхности пирамиды находиться как сумма площадей боковой поверхности и основания.
Г) Для нахождения объема нужно знать высоту пирамиды и площадь основания.
Оформление работы:

| Дано: SАВСД – пирамида, АВ=3см, ВС= 6см, пирамида неправильная, Н=10см, ℓ1=10,5см., ℓ2=10,2см Найти: Sб.п. Sп.п. V Решение: т.к. пирамида неправильная, то Sб.п. находят как сумму площадей ее боковых граней, т.е. площадей треугольников. S1 = 1/2 ·ℓ1·АВ=1/2·10,5·3=15,75(см2) - это площадь одной грани, а их две одинаковых, т.е S1,2 =15,75·2=31,5(см2) |
| S3=1/2·ℓ2·ВС= 1/2·10,2·6=30,6 (см2), S3,4=2·30,6=61,2(см2) Sб.п.= 31,5+61,2 =92,7(см2) Sосн.= АВ·ВС=3·6=18(см2), Sп.п.= Sб.п+ Sосн.= 92,7+18=110,7 (см2) (если пирамида правильная, то пользуемся формулами) V=1/3· Sосн·Н = 1/3·18·10 = 60(см3) – формула объема справедлива для любой пирамиды. | |
Задания для самостоятельной работы:
1. Сколько ребер у шестиугольной пирамида:
2. Какое наименьшее число граней может иметь пирамида:
3. В правильной четырехугольной пирамиде высота равна 4см, а длина диагонали основания - 6  см. Найдите площадь полной поверхности пирамиды.
см. Найдите площадь полной поверхности пирамиды.
4. Сколько граней у шестиугольной пирамиды:
5. Высота правильной треугольной пирамиды равна 12см, сторона основания 15см. Найти площадь полной поверхности пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Рис. 17
Для усеченной пирамиды справедливы формулы:

 (4)
(4)
где S1, S2 – площади верхнего и нижнего оснований;
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:

где p1 , p2 – периметры оснований;
hа – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).

|
Рис. 18
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами:  и
и 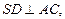 т.е.
т.е.  Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс
Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс  необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части:
необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части:  и
и  Из
Из  находим SO:
находим SO:  Из
Из  находим:
находим: 
Ответ: 
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны  см и
см и  см, а высота 4 см.
см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований 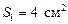 и
и 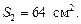 Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Подставив все данные в формулу, вычислим объем усеченной пирамиды:

Ответ: 112 см3.
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).

|
Рис. 19
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из 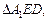 где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований.
где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. 

 так как
так как 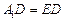 (см. рис. 20) и
(см. рис. 20) и 
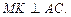 С другой стороны ОК – радиус вписанной в
С другой стороны ОК – радиус вписанной в  окружности и
окружности и  ОМ – радиус вписанной в
ОМ – радиус вписанной в 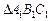 окружности:
окружности:

 MK = DE.
MK = DE.
По теореме Пифагора из 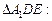

Площадь боковой грани: 
 Рис. 20
Рис. 20
Ответ: 
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j. Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей 


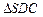 и площади трапеции ABCD.
и площади трапеции ABCD.
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
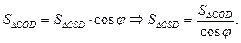

Рис. 21
Аналогично 

 и значит
и значит  Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
 Рис. 22
Рис. 22
Так как в трапецию можно вписать окружность, то  или
или  Из
Из 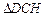 по теореме Пифагора имеем
по теореме Пифагора имеем



Тогда 
Площадь трапеции: 
Значит,

Ответ: 
Пример 5. Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.
Решение. Сделаем рисунок (рис. 23).

Рис. 23
Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( 
 ), два других – равные треугольники
), два других – равные треугольники  Рассмотрим
Рассмотрим 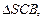


 – по условию. Вычислим его площадь:
– по условию. Вычислим его площадь:  Так как
Так как  равнобедренный, то
равнобедренный, то  а так как
а так как  то
то  и следовательно в
и следовательно в 


Тогда 
Рассмотрим 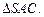
 SE найдем из
SE найдем из 
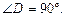 По теореме Пифагора имеем
По теореме Пифагора имеем  Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24).
Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24). 

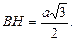 В
В  отрезок DE является средней линией, значит,
отрезок DE является средней линией, значит,  Находим SE:
Находим SE:


Рис. 24
Теперь 
Площадь боковой поверхности пирамиды равна:
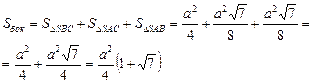
Ответ: 
|
из
5.00
|
Обсуждение в статье: Практическая работа №2 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

