 |
Главная |
Самостоятельная работа
|
из
5.00
|
1. Вычислить:
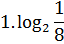
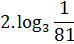
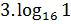
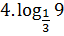
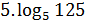
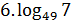
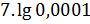


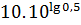
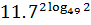

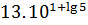
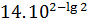
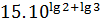
2. Упростить:
1. 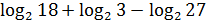
2. 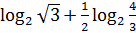
3. 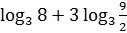
4. 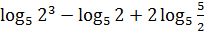
5. 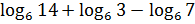
6. 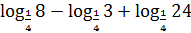
7. 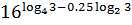
8. 
9. 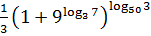
10. 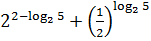
3.Сравнить:
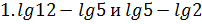
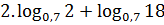 и
и 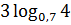
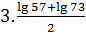 и
и 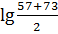
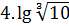 и lg2
и lg2
5.lg1.05 и lg (1.05)-2
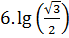 и
и 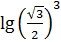
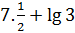 и lg20-lg3
и lg20-lg3
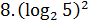 и
и 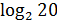
 и 4
и 4
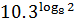 и
и 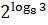
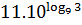 и
и 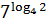
Практическая работа №4
Логарифмирование
Обучающая часть
Логарифмирование — действие, заключающееся в нахождении логарифма числа или выражения.
Логарифмирование является одним из двух действий, обратных возведению в степень. Если 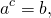 то
то 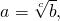
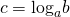
Методом логарифмирования могут быть решены некоторые логарифмические уравнения.
Решение уравнения логарифмированием схематически можно описать приблизительно так.
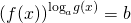
ОДЗ:
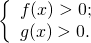
Логарифмируем обе части уравнения по основанию a:
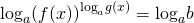
(просто приписываем к обеим частям уравнения логарифм по основанию a. a — основание логарифма, стоящего в показателе степени).
Показатель степени выносим за знак логарифма:
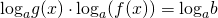
Примеры решения уравнений методом логарифмирования.
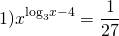
ОДЗ: x>0.
Логарифмируем обе части уравнения по основанию 3:
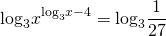
В левой части уравнения показатель степени выносим за знак логарифма. В правой части находим значение логарифма:
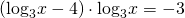
(Обратите внимание: показатель степени — разность. Сумму и разность при вынесении за знак логарифма обязательно нужно взять в скобки).
Полученное уравнение решаем с помощью замены переменной .
Пусть
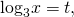 тогда
тогда
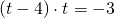
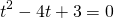
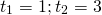
Обратная замена:
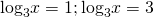
Эти простейшие логарифмические уравнения решаем по определению логарифма:
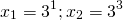
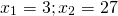
Ответ: 1; 27.
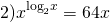
ОДЗ: x>0.
Логарифмируем обе части уравнения по основанию 2:
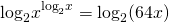
(Обратите внимание: произведение в правой части уравнения записываем в скобках).
В левой части уравнения показатель степени выносим за знак логарифма. В правой части от логарифма произведения переходим к сумме логарифмов:
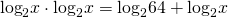
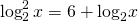
Пусть
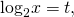 тогда
тогда
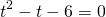
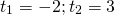
Возвращаемся к исходной переменной:
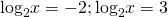
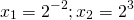
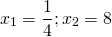
Ответ: 1/4; 8.

ОДЗ:
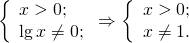
Прологарифмируем обе части уравнения по основанию 10:
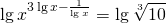
В левой части показатель степени выносим за знак логарифма. Логарифм в правой части вычисляем:
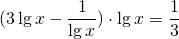
Замена
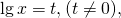
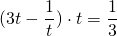
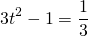
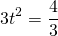

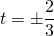
Обратная замена

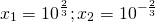
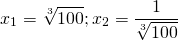
Ответ:
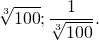
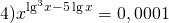
ОЗД: x>0.
Прологарифмируем обе части уравнения по основанию 10:
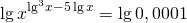
Показатель степени вынесем за знак логарифма
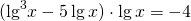
Здесь сначала удобно раскрыть скобки
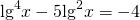
Замена
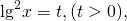
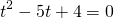
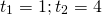
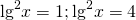
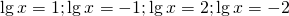
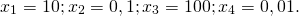
Самостоятельная работа
1. 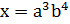
2. 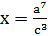
3. 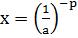
4. 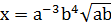
5. 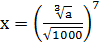
6. 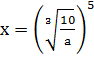
7. 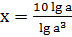
8. 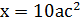
9. 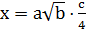
10. 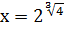
11. 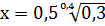
12. 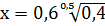
13. 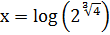
14. 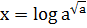
15. 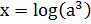
16. 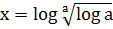
Тема 3
«Основы тригонометрии»
Практическая работа №1
Радианный метод измерения углов вращения и связь с градусной мерой
Обучающая часть
Перевод градусов в радианы и обратно.
1.
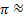 3,14
1°= 3,14
1°=  радиан радиан
|
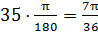
2. 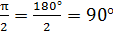
3. 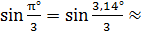 sin 1,05°
sin 1,05°
4. 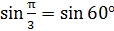
Четверть углов
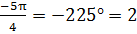 четверть
четверть
-30°= 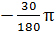 =
=  = 4 четверть
= 4 четверть
Определение знака выражения :
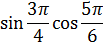
Переводим все углы в градусную меру , затем смотрим в какой координатной четверти лежит полученное число .
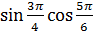 =
= 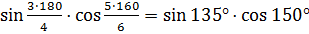
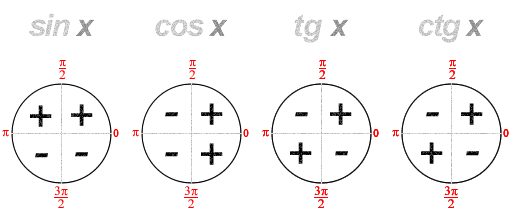 sin135°
sin135° 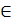 2 четверти(знак +)
2 четверти(знак +)
cos150° 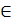 2 четверти(знак -)
2 четверти(знак -)
Следу правилу «минус на плюс даёт минус» получаем :
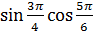 <0
<0
|
из
5.00
|
Обсуждение в статье: Самостоятельная работа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

