Обучающая часть работы.

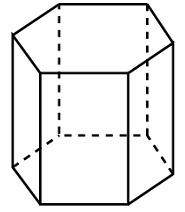
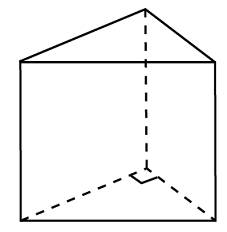
1.1. Призма:

Призма — многогранник, две грани которого являются многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.           

Виды призм

· Призма, основанием которой является параллелограмм, называется параллелепипедом.

· Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.

· Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.

· Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.

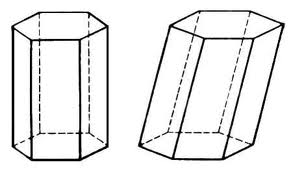
                                    прямая призма        наклонная призма

Свойства призмы:

· Основания призмы являются равными многоугольниками.

· Боковые грани призмы являются параллелограммами.

· Боковые ребра призмы параллельны и равны.

Площадь боковой поверхности прямой призмы: S_б.п. = P•H где P — периметр основания призмы (сумма всех сторон основания), H — высота призмы.

Объём призмы равен произведению её высоты на площадь основания: V = S_осн.•H

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания: S_п.п. = P•H +2• S_осн

Диагональ прямой призмы:  

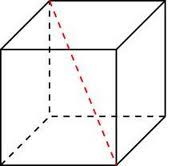Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его линейных размеров: d² = a² +b² +c²

Сечения призмы:                   диагональные сечения

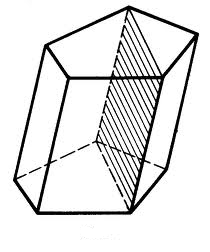
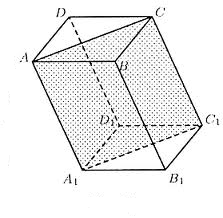
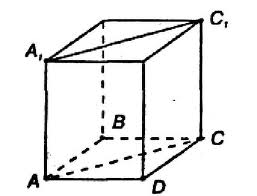
Сечения призмы под углом к плоскости основания:

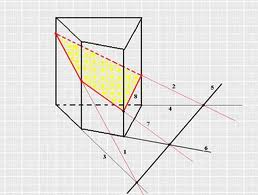
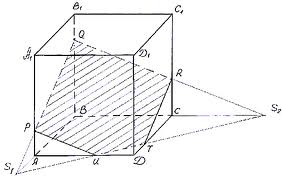
Сечение плоскостью перпендикулярной ребрам наклонной призмы:

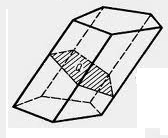
Пример 1: Найти площадь боковой, полной поверхности, объем призмы.

А) Для нахождения площади боковой поверхности призмы нужно измерить линейкой следующие элементы призмы: стороны основания, высоту. Подставить значения в формулу для нахождения пощади (если призма прямая). Если призма наклонная, то боковую поверхность находим из суммы площадей граней.

Б) Для нахождения площади полной поверхности призмы нужно найти площадь основания призмы (площадь треугольника, прямоугольника, ромба)

Площадь полной поверхности призмы находиться как сумма площадей боковой поверхности и двух оснований.

В) Для нахождения объема нужно знать высоту призмы и площадь основания.

Дано: АВСС1В1А1 треугольная призма, прямая, правильная АВ=ВС=АС = 5 см, Н = 10 см   Найти: Sб.п., Sп.п. V   Решение: Sб.п. = P•H Р=5+5+5=15, Н=10 Sб.п.= 15•10 = 150 (см2)   Фо́рмула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, b, c: Sосн= √р(р-а)(р-в)(р-с) где p — полупериметр треугольника: р = (а+в+с):2 р= 15:2 =7,5

Sосн= √7,5(7,5-5)(7,5-5)(7,5-5)= 7,7 (см2) Sп.п. = P•H +2• Sосн, = 150 + 2•7,7 = 164,4 (см2) V = Sосн.•H = 7,7•10 =77 (см3) Пример2.Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 10. Решение: Площадь боковой поверхности правильной шестиугольной призмы складывается из площадей 6-ти равных прямоугольников (одна сторона прямоугольника – сторона основания, вторая – высота призмы). S=6*3*10=180. Ответ: 180. Пример3.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 20, боковое ребро равно 5. Найдите объем призмы. Решение: Объем призмы вычисляется по следующей формуле: V=Sосн*H (H– высота, в данном случае и боковое ребро прямой призмы). При этом в основании – прямоугольный треугольник, площадь которого находится как полупроизведение катетов: Sосн=1/2*8*20=80 Тогда V=80*5=400. Ответ: 400.

Задания для самостоятельной работы:

1. Сколько ребер у шестиугольной призмы?

2. Какое наименьшее число граней может иметь призма?

3. Какое наименьшее число ребер может иметь призма?

4.Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 4, а высота — 15.

5. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 4, боковые рёбра равны 12. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1

6.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы.