 |
Главная |
Вычисление площадей плоских фигур.
|
из
5.00
|
Цель: Применять определенный интеграл для вычисления площадей, длин и объемов фигур.
Теоретические сведения к практической работе
Площади плоских фигур
1. Вычисление площадей плоских фигур в декартовой системе координат
Если плоская фигура (рис. 1) ограничена линиями 
 , где
, где  для всех
для всех  , и прямыми
, и прямыми  ,
,  , то ее площадь вычисляется по формуле:
, то ее площадь вычисляется по формуле:
 (8)
(8)

| 
|
| Рис. 1 | Рис. 2 |
Пример. Найти площадь фигуры, ограниченной линиями:

Решение. Построим схематический рисунок (рис. 2). Для построения параболы возьмем несколько точек:
| x | 0 | 1 | –1 | 2 | –2 | 3 | –3 | 4 | –4 |
| y | –2 | –1 | –1 | 2 | 2 | 7 | 7 | 14 | 14 |
Для построения прямой достаточно двух точек, например  и
и  .
.
Найдем координаты точек  и
и  пересечения параболы
пересечения параболы 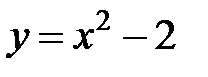 и прямой
и прямой 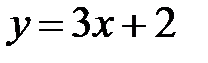 .
.
Для этого решим систему уравнений

Тогда  Итак,
Итак, 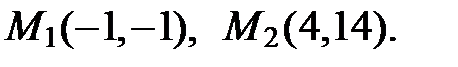
Площадь полученной фигуры найдем по формуле (8), в которой
 поскольку
поскольку  для всех
для всех  . Получим:
. Получим:

2. Вычисление площадей фигур, ограниченных линиями, заданными параметрически
Если функции  и
и  имеют непрерывные производные первого порядка для всех
имеют непрерывные производные первого порядка для всех  , то площадь плоской фигуры, ограниченной линией
, то площадь плоской фигуры, ограниченной линией  прямыми x = a, x = b, где a = x(t0),
прямыми x = a, x = b, где a = x(t0),
b = x(t1), и осью OX, вычисляется по формуле:
 (9)
(9)
Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически:

Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра 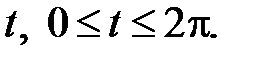
| t | 0 | 
| 
| 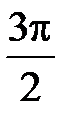
| 
|
| x | 2 | 0 | –2 | 0 | 2 |
| y | 0 | 3 | 0 | –3 | 0 |

|
| Рис. 3 |
Нанесем точки (x, y) на координатную плоскость XOY и соединим плавной линией. Когда параметр  изменяется от
изменяется от  до
до  , соответствующая точка
, соответствующая точка  описывает эллипс (известно, что
описывает эллипс (известно, что  — параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдем её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (9) получим:
— параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдем её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (9) получим:

Длина дуги плоской кривой
1. Вычисление дуги плоской кривой в декартовых координатах

|
| Рис. 4 |
Если кривая задана уравнением  , функция
, функция 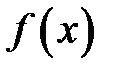 имеет непрерывную первую производную при всех
имеет непрерывную первую производную при всех  , то длина дуги
, то длина дуги  (рис. 4) этой кривой, заключенной между точками
(рис. 4) этой кривой, заключенной между точками  и
и  , вычисляется по формуле:
, вычисляется по формуле:
 (10)
(10)
2. Вычисление длины дуги кривой, заданной параметрически
Если кривая задана параметрически  , и функции
, и функции  имеют непрерывные производные 1-го порядка при всех
имеют непрерывные производные 1-го порядка при всех  , то длина дуги
, то длина дуги  , соответствующей изменению параметра от
, соответствующей изменению параметра от  до
до  , вычисляется по формуле:
, вычисляется по формуле:
 (11)
(11)
Пример. Найти длину дуги кривой
а)  б)
б) 
Решение.
а) Так как кривая задана в декартовой системе координат уравнением  , то для вычисления длины дуги воспользуемся формулой (10). Найдем
, то для вычисления длины дуги воспользуемся формулой (10). Найдем  :
:  и подставим в (10):
и подставим в (10):

б) 
Кривая задана параметрически, поэтому воспользуемся формулой (11). Найдем  :
:
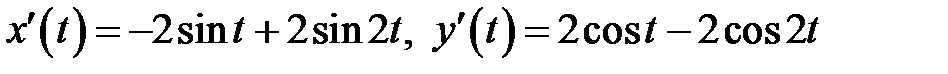 и подставим в (11):
и подставим в (11):

Вычисление объемов тел вращения
Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой  , осью OX и прямыми
, осью OX и прямыми  ,
,  (рис. 5), то его объем вычисляется по формуле:
(рис. 5), то его объем вычисляется по формуле:
 (12)
(12)

| 
|
| Рис. 5 | Рис. 6 |
Пример. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: 
Решение. Построим криволинейную трапецию, вращением которой получается тело вращения (рис. 6).
Чтобы получить объем тела вращения из объема  тела, полученного вращением фигуры ОАВС, вычтем объем
тела, полученного вращением фигуры ОАВС, вычтем объем 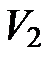 тела, полученного вращением фигуры ОАВ. Тогда искомый объем
тела, полученного вращением фигуры ОАВ. Тогда искомый объем  . По формуле (12) найдем
. По формуле (12) найдем  и
и  :
:  (ед. объема);
(ед. объема);
 (ед. объема);
(ед. объема);
 (ед. объема).
(ед. объема).
Содержание практической работы
Задание 1. Найти площадь фигуры, ограниченной линиями.
1) 
2) 
3) 
4) 
5) 
6) 
Задание 2. Найти площадь фигуры, ограниченной линиями, заданными параметрически.
1) 
2) 
3) 
4) 
5) 
6) 
Задание 3. Найти длину дуги кривой.
1) 
2) 
3) 
4) 
5) 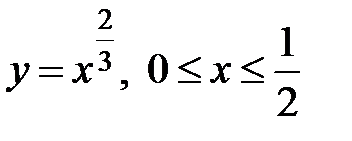
6) 
Задание 4. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями.
1) 
2) 
3) 
4) 
5) 
6) 
Тема 10
«Координаты и векторы»
Обучающая часть
Вектор - направленный отрезок.
Обозначение АВ или а.
А - начало вектора, В - конец.
Нулевой вектор - вектор, начало и конец которого совпадают.
Обозначение ММ или б.
Длиной вектора (абсолютной величиной вектора) называется длина отрезка.
Обозначение АВ или а .
Коллинеарные векторы - ненулевые векторы, которые лежат
на одной прямой или на параллельных прямых.
Если коллинеарные векторы направлены в одну сторону относительно
прямой, проходящей через их начало, то векторы называются
сонаправленными, если в разные стороны - то противоположно
направленными.
Действия с векторами
1) а+ b= b+ а - переместительный закон
2) (а+ b)+ с= а+ (b+ с) - сочетательный закон
3) (kI)a= к× (Iа)= I• (ка) - сочетательный закон
4) (к+ I) a= k-a+ l×a - I распределительный закон
5) к×(а+ b)= ka + кb - II распределительный закон


Скалярным произведением двух векторов называется произведение их длина косинус угла между ними. 
Уравнение окружности
( х - х 0 ) 2 + ( у - у 0 ) 2=/?2
(х0, у0) - координаты центра окружности, R - радиус.
Если центр окружности лежит в начале системы координат,
то уравнение имеет вид: х2+у2= R 2

Обучающая часть
Понятие вектора
Векторы занимают особое место среди объектов, рассматриваемых в высшей математике, поскольку каждый вектор имеет не только числовое значение - длину, но и физическое и геометрическое - направленность. Вектор, представленный направленным отрезком, идущим от точки A к точке B, обозначается так:  .
.

Вектор - это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1(левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в искомой точке.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
 Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка, т.е. отрезка, у которого различают начало и конец.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка, т.е. отрезка, у которого различают начало и конец.
Если A - начало вектора, а B - его конец, то вектор обозначается символом  или одной строчной буквой
или одной строчной буквой  . На рисунке конец вектора указывается стрелкой (рис. 1)
. На рисунке конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора  называется длина порождающего его отрезка
называется длина порождающего его отрезка 
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
|
из
5.00
|
Обсуждение в статье: Вычисление площадей плоских фигур. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

