Задачи с применением формул комбинаторики

 

Цель: Научиться решать задачи на нахождение вероятностей

Теоретические сведения к практической работе

Классическое определение вероятности

Раздел математики, изучающий закономерности случайных событий, называется теорией вероятностей.

Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называют отношение числа исходов m, благоприятствующих событию А, к числуn всех исходов испытания.

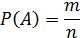
Пример 1: В партии из 30 миксеров 2 бракованных. Найти вероятность купить исправный миксер.

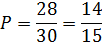
Аксиомы вероятностей:

Каждому событию А поставлено в соответствие неотрицательное число Р(А), называемое вероятностью события А.

Если события А₁, А₂ … попарно несовместны, то Р(А₁+А₂+…)=Р(А₁)+Р(А₂)+…

Свойства вероятностей:

Вероятность невозможного события равна нулю Р=0.

Вероятность достоверного события равна единице Р=1.

Вероятность произвольного случайного события А заключается между 0 и 1: 0<Р(А)<1.

Пример 2: Из 34 экзаменационных билетов, пронумерованных с помощью чисел от 1 до 34, наудачу извлекается один. Какова вероятность, что номер вытянутого билета есть число, кратное трем.

Решение: Найдем количество чисел от 1 до 34, кратных трем. Это числа 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33. Всего таких чисел 11. Таким образом, искомая вероятность

События А и В называются совместными, если они могут одновременно произойти, и несовместными, если при осуществлении одного события не может произойти другое.

События А и В называются независимыми, если вероятность наступления одного события не зависит от того, произошло другое событие или нет.

Вероятность суммы двух совместных событий равна сумме вероятностей слагаемых без вероятности произведения: Р(А+В)=Р(А)+Р(В)-Р(АВ)

Пример 3: Вероятность поражения одной мишени – 0,7, а другой – 0,8. Какова вероятность, что будет поражена хотя бы одна мишень, если по ним стреляют независимо друг от друга.

Решение: Т.к. события совместны, то

Вероятность суммы двух несовместных событий равна сумме вероятностей слагаемых: Р(А+В)=Р(А)+Р(В).

Р(А)+Р( )=1

Условная вероятность – вероятность одного события, при условии, что другое событие уже произошло.

Вероятность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого: Р(АВ)=Р(А)∙Р(А/В) или Р(ВА)=Р(А)∙Р(В/А)

Вероятность произведения двух независимых событий А и В равна произведению вероятностей сомножителей: Р(АВ)=Р(А)∙Р(В).

    Пример 4: В двух коробках лежат ручки разного цвета. В первой коробке – 4 красных и 6 черных, во второй – 3 красных, 5 синих и 2 черных. Из обеих коробок вынимают по одной ручки. Найти вероятность, что обе ручки красные.

Решение: Найдем вероятности вытащить красную ручку из каждой коробки

Тогда вероятность того, что обе ручки красные:

Полная вероятность. Формула Байеса

Если событие А может произойти только при выполнении одного из событий Н₁, Н₂, …, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

Эта формула называется формулой полной вероятности.

Если выполняются все условия, имеющие место для формулы полной вероятности, и 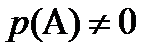, то выполняется равенство, называемое формулой Байеса:

Пример 1: В первой партии 20 ламп, во второй – 30 ламп и в третьей – 50 ламп. Вероятности того, что проработает заданное время, равна для первой партии 0,7, для второй – 0,8 и для третьей партии – 0,9. Какова вероятность того, что наудачу взятая лампа проработает заданное время? Найти вероятность, что эта лампа принадлежит первой партии?

Решение: Пусть событие А – наудачу взятая лампа проработает заданное время.

Тогда, пусть Н₁ – лампа из первой партии, Н₂ – лампа из второй партии и Н₃ – лампа из третьей партии. Тогда событие А/Н₁ – лампа из первой партии проработает заданное время, А/Н₂ – лампа из второй партии проработает заданное время и А/Н₃ – лампа из третьей партии проработает заданное время. Найдем вероятности

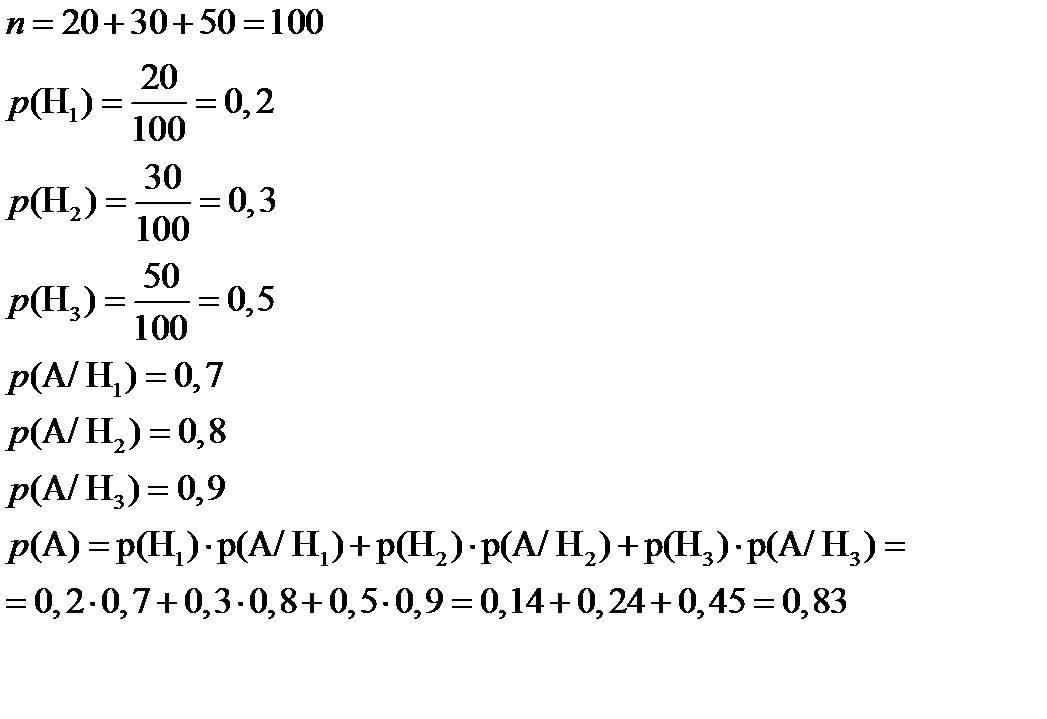
Теперь, используя формулу Байеса найдем вероятность того, что эта лампа принадлежит первой партии

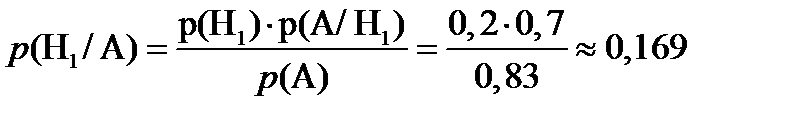
Пример 2: Имеются 3 одинаковые урны. В первой урне находятся 5 белых и 7 черных шаров, во второй – только белые и в третьей – только черные. Наугад выбираются урна и из нее извлекается один шар. Какова вероятность, что этот шар белый?

Решение: Пусть событие А – извлекается белый шар.

Тогда, пусть Н₁ – шар из первой урны, Н₂ – шар из второй урны и Н₃ – шар из третьей урны. Тогда событие А/Н₁ – белый шар из первой урны, А/Н₂ – белый шар из второй урны и А/Н₃ – белый шар из третьей урны. Найдем вероятности

Формула Бернулли

1) Вероятность того, что событие А наступит ровно m раз при проведении n независимых испытаний, каждый из которых имеет ровно два исхода вычисляется по формуле Бернулли

Пример 1: Вероятность выигрыша по одному лотерейному билету равна 0,2. Найти вероятность, что из 6 приобретенных билетов 2 окажутся выигрышными.Решение:

2) Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, удовлетворяющих схеме Бернулли, равна

Пример 2: Прибор состоит из шести элементов, работающих независимо друг от друга. Вероятность безотказной работы каждого элемента за определенное время равна 0,6. Для безотказной работы прибора необходимо, чтобы хотя бы один элемент был исправен. Какова вероятность, что за данное время прибор будет работать безотказно?

Решение:

3) Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, удовлетворяющих схеме Бернулли, наступит не менее m₁ и не более m₂ раз вычисляется по формуле

Пример 3: Найти вероятность осуществления от двух до четырех разговоров по телефону при наблюдении пяти независимых вызовов, если вероятность того, что разговор состоится, равна 0,7.

Решение:

4) Наивероятнейшее значение m₀ числа наступления события А при проведении n повторных независимых испытаний, удовлетворяющих схеме Бернулли, вычисляется по формуле

Пример 4: Магазин получил 50 деталей. Вероятность наличия нестандартной детали в партии равна 0,05. Найти наиболее вероятное число нестандартных деталей в партии.

Решение:

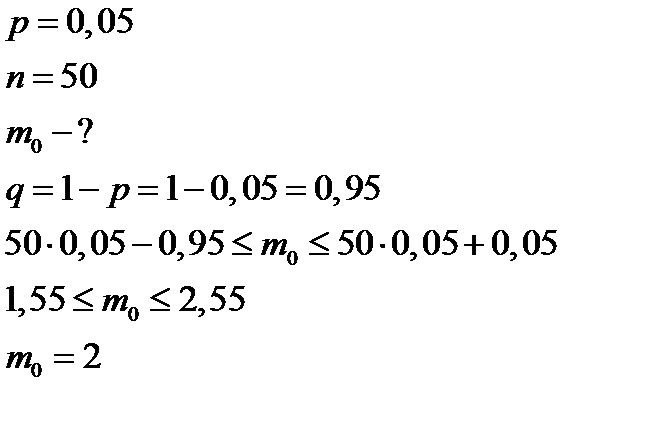
Дискретная случайная величина и ее числовые характеристики

Случайная величина Х – это числовая функция , определенная на пространстве элементарных событий. Случайные величины, имеющие счетные множества возможных значений, называются дискретными. Дискретная случайная величина определена, если известны все ее значения и соответствующие им вероятности. Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называют распределением вероятностей случайной величины. Для дискретной случайной величины это соответствие может быть записано в виде таблицы:

xi	x1	x2	…	xn
pi	p1	p2	…	pn

 

Математическим ожиданием (средним значением) дискретной случайной величины Х называют сумму произведений всех ее возможных значений на соответствующие им вероятности

Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания . Дисперсия дискретной случайной величины вычисляется по формулам:

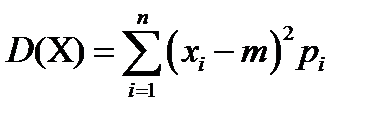
Средним квадратичным отклонением дискретной случайной величины называют корень квадратный из дисперсии .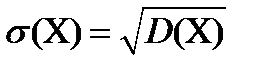

Если случайная величина Х имеет биномиальное распределение вероятностей, то

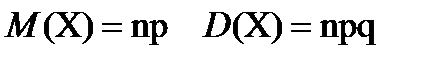
Пример 1: Случайная величина Х задана таблицей распределения вероятностей. Найти М(Х), D(Х), σ(Х).

хi	2	5	8	9
рi	0,1	0,4	0,3	0,2

Решение:

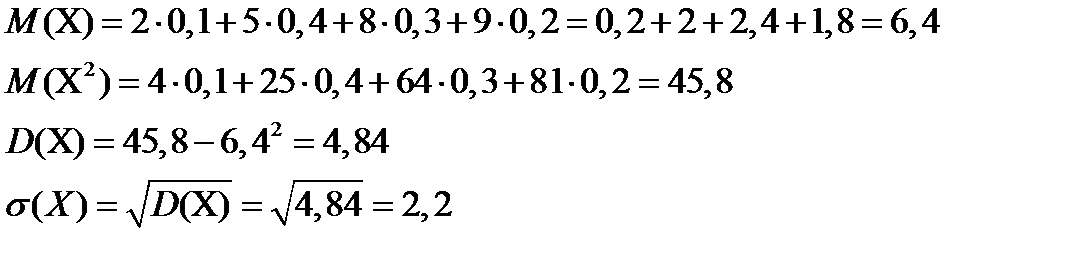
Пример 2: Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 100 билетов, а вероятность выигрыша на каждый билет равна 0,05.

Решение:

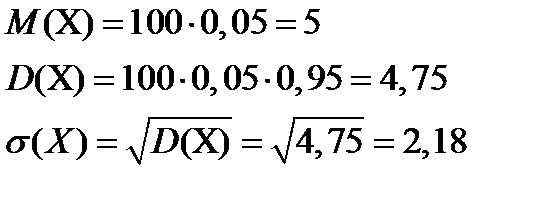
Содержание практической работы

Задание 1. Используя классическое определение вероятности события, решить следующие задачи:

1. В коробке 4 красных, 5 зеленых, 8 желтых, 7 белых и 1 черный шар. Найти вероятность вытащить: красный шар; синий шар; белый шар; цветной шар; или зеленый или белый шар; не красный шар; шар одного из цветов светофора.

2. В семье – двое детей. Какова вероятность, что старший ребенок – девочка, если известно, что в семье есть дети обоего пола?

3. Мастер, имея 10 деталей, из которых 4 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?

4. В одном ящике 3 белых и 7 черных шаров, в другом ящике – 6 белых и 8 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.

5. Издательство отправило газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,9, во второе - 0,7, в третье - 0,85. Найти вероятность следующих событий:

а) только одно отделение получит газеты вовремя;

б) хотя бы одно отделение получит газеты с опозданием.

6. В первой урне находятся 12 белых и 4 черных шаров, а во второй 5 белых и 10 черных шаров. Из каждой урны вынули по шару. Какова вероятность того, что оба шара окажутся черными? Какова вероятность, что оба шара окажутся белыми?

7. В партии из 25 деталей находятся 8 бракованных. Вынимают из партии наудачу две детали. Определить, какова вероятность того, что обе детали окажутся бракованными.

8. Подброшены две игральные кости. Найти вероятность события A того, что выпадет хотя бы одна шестерка.

9. Найти вероятность, что при бросании игральной кости выпадет число, большее 4.

10. Найти вероятность, что при бросании игральной кости выпадет число, не меньшее 2 и не большее 5.

Задание 2. Используя формулы полной вероятности и Байеса, решить следующие задачи:

1. Имеются 2 одинаковые урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 6 белых и 4 черных. Наугад выбираются урна и из нее извлекается один шар. Выбранный шар оказался черным. Какова вероятность, что этот шар из 2 урны?

2. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру =0,5, ко второму =0,6. Вероятность того, что годная деталь будет признана стандартной первым контролером =0,94, а вторым =0,92. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

3. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная равна 0,9, а второго – 0,8. Найти вероятность того, что взятая наудачу деталь – стандартная.

4. Имеются 3 одинаковые урны. В первой урне находятся 6 синих и 4 черных шаров, во второй – только синие и в третьей – только черные. Наугад выбираются урна и из нее извлекается один шар. Какова вероятность, что этот шар синий?

5. Имеются 2 одинаковые урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 6 белых и 4 черных. Наугад выбираются урна и из нее извлекается один шар. Выбранный шар оказался черным. Какова вероятность, что этот шар из 1 урны?

Задание 3. Используя формулу Бернулли, решить следующие задачи:

1. Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

2. Найти вероятность осуществления от одного до трех разговоров по телефону при наблюдении шести независимых вызовов, если вероятность того, что разговор состоится, равна 0,6.

3. Прибор состоит из пяти элементов, включенных в цепь параллельно и работающих независимо друг от друга. Вероятность безотказной работы каждого элемента за время Т равна 0,5. Для безаварийной работы прибора достаточно, чтобы хотя бы один элемент был исправен. Какова вероятность того, что за время Т прибор будет работать безотказно?

4. Вероятность выигрыша по одному лотерейному билету =0,3. Какова вероятность того, что из семи приобретенных билетов три билета окажутся выигрышными?

5. Магазин получил 40 деталей. Вероятность наличия нестандартной детали в партии равна 0,04. Найти наиболее вероятное число нестандартных деталей в этой партии.

6. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найдя вероятности возможного числа появления бракованных деталей среди 5 отобранных, найти наивероятнейшее число появления бракованных деталей из 5 отобранных, указав его вероятность.

7. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было равно 10?

8. Для данного участника игры вероятность набросить кольцо на колышек =0,3. Какова вероятность того, что при шести бросках 3 кольца окажутся на колышке?

9. На самолете имеются 4 одинаковых двигателя. Вероятность нормальной работы каждого двигателя в полете равна р. Найти вероятность того, что в полете могут возникнуть неполадки в одном двигателе.

10. Вероятность отказа каждого прибора при испытании равна 0,4. Что вероятнее ожидать: отказ двух приборов при испытании четырех или отказ трех приборов при испытании шести, если приборы испытываются независимо друг от друга?

11. Вероятность того, что на некотором предприятии расход электроэнергии не превысит суточной нормы равна 0,8. Какова вероятность того, что в течение пяти рабочих дней из семи перерасхода электроэнергии не будет?

Задание 4. Найти числовые характеристики дискретных случайных величин:

1. Найти математическое ожидание случайной величины Х, зная закон ее распределения:

хi	3	5	2
рi	0,1	0,6	0,3

2. Вероятность попадания в цель при стрельбе из орудия 0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

3. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

хi	1	2	5
рi	0,3	0,5	0,2

 

4.Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

хi	2	3	5
рi	0,1	0,6	0,3

 

5. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины Х – числа появления события в этих испытаниях.

Тема 12
«Элементы теории вероятности и математической статистики»