ДИАГРАММЫ ЭЙЛЕРА-ВЕННА

Множеством называют всякую вполне определенную совокупность различаемых объектов. Например, «множество всех натуральных чисел», «множество букв русского алфавита», «множество действительных корней уравнения », «множество людей, побывавших на Луне в
XX веке».

Множества состоят из элементов. Договоримся для обозначения множеств использовать заглавные буквы латинского алфавита (A , B , C и т.д.), а для обозначения элементов множеств – строчные буквы латинского алфавита, возможно с индексом  и т.д.)

Запись  читается «  принадлежит А» и означает, что  является элементом множества А. Если  не является элементом множества А, то пишут – «  не принадлежит А».

Множество, которое не содержит ни одного элемента, называется пустым и обозначается . Множество называется непустым, если оно содержит хотя бы один элемент.

Множества A и B называются равными, если они состоят из одних и тех же элементов:

.

(Символ  читается «равносильно по определению».)

Имеем

,

«А – непустое множество» Û .

Говорят, что множество А содержится в множестве В (или, что А включается в множество В, или что А – подмножество множества В) и пишут , если каждый элемент множества А является элементом множества В: .

Теорема 1.1. Для любых множеств А, В, С имеют место следующие соотношения:

1)  (рефлексивность включения);

2)  (транзитивность включения);

3)  (антисимметричность включения). „

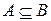Говорят, что множество А строго включается в множество В и пишут , если  и :

.

Пусть  («омега») – некоторое фиксированное непустое множество. Будем называть  универсальным множеством и считать, что все множества, которые далее будут нам встречаться, являются подмножествами множества .

Для изображения подмножеств множества  удобно использовать диаграммы Эйлера-Венна. Вот примеры таких диаграмм для множеств ,  и непустого :

Совокупность всех подмножеств произвольного множества А обозначается :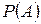

.

Понятно, что  и  для произвольного множества А.

Множество  называется конечным, если оно имеет конечное число элементов. Конечное –элементное  множество А можно задать путем перечисления всех его элементов:

.

При этом число  называется мощностью множества А и обозначается .

По определению считают, что мощность пустого множества  равна нулю: .

Множество  называют бесконечным, если оно не является конечным. Бесконечные множества задают, указывая то свойство , которое определяет принадлежность элемента  данному множеству:

 «А состоит из тех и только тех элементов множества , которые обладают свойством », т.е.  (запись « » читается «х обладает свойством »).

Пример 1.4.

1)

2)  – множество всех натуральных четных
чисел.

Используя этот способ, можно задавать и конечные множества. Например, множество С действительных корней уравнения  можно задать так: .

Понятно, что .

Операции над множествами

Пусть .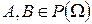

Дополнением множества А называется множество  (символ «:=» читается «равно по определению»).

Пересечением множеств А и В называется множество

.

Объединением множеств А и В называется множество

.

Разностью множеств А и В называется множество

.

Симметрической разностью множеств А и В называется множество

 АDВ:=(А\В)È(В\А).

Вот диаграммы Эйлера-Венна для множеств , , АÈВ, А\В, АDВ:

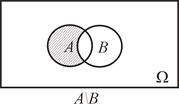
Теорема 1.2. Пусть А, В, СÎР(W). Тогда имеют место следующие равенства:

I 1) АÈА=А; 2) АÇА=А (идемпотентность операций È и Ç);

II 1) АÈВ=ВÈА; 2) АÇВ=ВÇА (коммутативность операций È и Ç);

III 1) (АÈВ)ÈС=АÈ(ВÈС); 2) (АÇВ)ÇС=АÇ(ВÇС) (ассоциативность операций È и Ç);

IV 1) АÈ(АÇВ)=А; 2) АÇ(АÈВ)=А (законы поглощения);

V 1) АÈ(ВÇС)=(АÈВ)Ç(АÈС) (дистрибутивность операции È относительно операции Ç);

2) АÇ(ВÈС)=(АÇВ)È(АÇС) (дистрибутивность операции Ç относительно операции È);

VI 1) АÈÆ=А; АÇÆ=Æ; 2) АÈW=W; АÇW=А (свойства Æ и W);

VII 1) Æ; 2) (cвойства дополнения);

VIII  (инволютивность дополнения);

IX 1) ; 2) (законы Де Моргана).

Для доказательства перечисленных равенств можно использовать метод диаграмм. Докажем, например, этим методом первый закон
Де Моргана

.

Изображаем последовательно диаграммы Эйлера-Венна для множеств А, В, АÈВ, : (на каждой диаграмме должны быть оба множества А и В):

Теперь изображаем последовательно диаграммы Эйлера-Венна для множеств А, В, , , :

Совпадение финальных диаграмм полученных цепочек и доказывает нужное равенство. „