Глава 1. Множества и отношения

В.Н. Салий, М.М. Кац, В.И. Лаврушин, И.Д. Сагаева

 

 

ДИСКРЕТНАЯ МАТЕМАТИКА

Учебное пособие

для студентов заочного отделения

механико-математического факультета

 

 

Издательство Саратовского университета

2003

УДК 519.7

ББК 22.14я73

С16

 

 

Салий В. Н., Кац М. М., Лаврушин В. И., Сагаева И. Д.

С16 Дискретная математика: Учеб. пособие для студентов заоч. отд-ния мех.-мат. фак. – Саратов: Изд-во Сарат. ун-та, 2003. – 56 с.: ил. (Б-ка “Основы математики”; Вып. 15).

       ISBN 5-292-

 

В пособии излагаются основные факты из алгебры множеств и отношений, рассматриваются простейшие свойства автоматов, приводятся начальные сведения о булевых функциях. Разбор примеров и самостоятельное решение контрольных заданий помогут лучшему усвоению теоретического материала.

Для студентов, изучающих курс дискретной математики, и всех, интересующихся ее приложениями.

 

Рекомендуют к печати:

               

Кафедра математической кибернетики и компьютерных наук

Саратовского государственного университета

Доктор физико-математических наук, профессор Д. А. Бредихин

 

 

УДК 519.7

ББК 22.14я73

 

Работа издана в авторской редакции

 

ISBN 5-292-                                                  Ó В. Н. Салий, М. М. Кац, В. И. Лаврушин,

И. Д. Сагаева, 2003

 

 

Учебное издание

 

Салий Вячеслав Николаевич, Кац Михаил Матвеевич,

Лаврушин Владимир Иванович, Сагаева Ирина Дмитриевна

 

ДИСКРЕТНАЯ МАТЕМАТИКА

 

Учебное пособие для студентов заочного отделения

Механико-математического факультета

 

Библиотека “Основы математики”. Выпуск 15

 

Ответственный за выпуск В. А. Иванов

Технический редактор Л. В. Агальцова

 

Подписано в печать 27.03.2003. Формат 60x84 1/16. Бумага офсетная. Гарнитура Таймс. Печать офсетная. Усл. печ. л. 3,25(3,5). Уч.-изд. л. 3,4. Тираж 150 экз. Заказ

Издательство Саратовского университета. 410026, Саратов, Астраханская, 83.
Типография Издательства Саратовского университета.
410026, Саратов, Астраханская, 83.

 

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ ........................................................................................................................      4

Глава 1. Множества и отношения .................................................................................      5

1.1. Высказывания. Логические операции. Предикаты. Кванторы ............      5

1.2. Понятие множества. Способы задания множеств. Операции над мно-

  жествами. Диаграммы Эйлера-Венна ........................................................      8

1.3. Двоичная булева алгебра. Конечные множества и двоичные булевы

  векторы ..........................................................................................................    12

1.4. Декартово произведение множеств и бинарные отношения между

  множествами .................................................................................................    13

1.5. Бинарные отношения на множестве ...........................................................    15

1.6. Бинарные отношения на конечных множествах,  ориентированные

  графы и двоичные булевы матрицы ...........................................................    17

1.7. Свойства бинарных отношений ..................................................................    19

1.8. Классы бинарных отношений .....................................................................    21

Глава 2. Элементы теории автоматов .........................................................................    27

2.1. Основные понятия теории автоматов......................................................... 27

2.2. Минимизация конечных автоматов............................................................. 34

Глава 3. Алгебра логики .................................................................................................    40

3.1. Функции алгебры логики. Табличное и цепочное задание функций.

  Элементарные функции. Формулы алгебры логики................................ 40

3.2. Эквивалентность формул. Логические операции и их свойства.

  Принцип двойственности. Разложение булевых функций по перемен-

  ным. Совершенные дизъюнктивные и конъюнктивные нормальные

  формы.............................................................................................................. 44

3.3. Полнота и замкнутость.................................................................................. 47

Библиографический список ................................................................................................    50

Контрольная работа ........................................................................................................    51

Приложение ........................................................................................................................    54

 

ВВЕДЕНИЕ

 

Пособие предназначено для студентов заочного отделения механико-математического факультета, обучающихся по специальностям «Прикладная информатика в экономике», «Прикладная информатика в юриспруденции». Оно состоит из трех глав, разбитых на параграфы. Первая глава «Множества и отношения» является базовой для всего курса. Вторая и третья главы посвящены изучению элементов двух важнейших разделов дискретной математики – теории конечных автоматов и алгебры логики. Для лучшего усвоения материала многие из приводимых понятий и утверждений иллюстрируются примерами. Из-за ограниченности объема пособия почти все теоремы даны без доказательств. Доказательства приведенных теорем и дальнейшую информацию по затронутым вопросам можно найти в литературе, список которой дан в конце пособия. Предлагаемая контрольная работа поможет студентам закрепить полученные знания.

 

 

Глава 1. Множества и отношения

 

1.1. ВЫСКАЗЫВАНИЯ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ.

ПРЕДИКАТЫ. КВАНТОРЫ

 

Высказывание – это повествовательное предложение, о котором можно судить, истинно оно или ложно.

Пример 1.1. Высказываниями будут следующие предложения:

1) « » (истинное высказывание);

2) « » (ложное высказывание);

3) «1000 – четное число» (истинное высказывание);

4) «уравнение  имеет два различных действительных корня» (истинное высказывание);

5) «существует прямоугольный треугольник со сторонами 3, 4, 6» (ложное высказывание);

6) «любые две прямые на плоскости параллельны» (ложное высказывание);

7) «Саратовский государственный университет основан в 1909 году» (истинное высказывание).

Высказывания будем обозначать строчными латинскими буквами, например p , q , r , …

Введем две логические константы: и – «истина» и л – «ложь». Каждому высказыванию p поставим в соответствие логическую константу  по правилу:

 

Логическая константа  называется логическим значением высказывания p.

Логические операции (или связки) позволяют получать новые высказывания из уже имеющихся. Операции подразделяются на унарные
(т.е. применяемые к одному аргументу – высказыванию) и бинарные
(т.е. применяемые к двум аргументам – высказываниям). Перечислим логические операции.

 

Название операции	Символ операции	Тип операции
Отрицание		Унарная
Конъюнкция (логическое умножение)	&	Бинарная
Дизъюнкция (логическое сложение)	Ú	Бинарная
Импликация (логическое следование)	Þ	Бинарная
Эквивалентность (логическое равенство)	Û	Бинарная

 

Приведем некоторые способы прочтения выражений, получающихся из высказываний при помощи логических операций (ниже p и q – произвольные высказывания).

 

Выражение	Способы прочтения
	«не p», «неверно, что p»
	«p и q»
	«p или q»
	«если p, то q», «p влечет q», «из p следует q»
	«p равносильно q», «p тогда и только тогда, когда q»

 

Логическое значение  высказывания  вычисляется согласно следующей таблице.

 

и	л
л	и

 

Логические значения высказываний , , ,  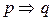вычисляются в зависимости от логических значений высказываний p и q, согласно следующей таблице.

 

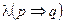
и	и	и	и	и	и
и	л	л	и	л	л
л	и	л	и	и	л
л	л	л	л	и	и

 

Предикатом от перем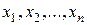енных  называется всякое предложение, зависящее от переменных 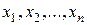, которое после подстановки вместо указанных переменных произвольных допустимых значений превращается в высказывание.

Предикаты, зависящие от n переменных , называются n -местными и обозначаются ,  и т.д.
Нуль-местными предикатами называются высказывания.

Пример 1.2.

1. Рассмотрим одноместный  предикат : , где переменная x может принимать любые действительные значения. При  предикат  превращается в истинное высказывание : , а при  – в ложное высказывание : .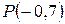

2. Рассмотрим двуместный  предикат : , где переменные  и  могут принимать любые целочисленные значения.

Имеем:

а) : – истинное высказывание,

б) : – истинное высказывание,

в) : – ложное высказывание.

3. Рассмотрим четырехместный  предикат , где переменные  и  могут принимать любые действительные значения, переменная  может быть произвольным ненулевым действительным числом, а переменная  – любым целым неотрицательным числом. При этом  означает: «квадратное уравнение  имеет  различных действительных корней». Имеем:

а) : «квадратное уравнение  имеет 1 действительный корень» – истинное высказывание;

б) : «квадратное уравнение 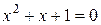 имеет нуль действительных корней» – истинное высказывание;

в) : «квадратное уравнение  имеет нуль действительных корней» – ложное высказывание.

С использованием логических операций  можно получать новые предикаты из уже имеющихся.

Пример 1.3.

1) : ;

2) : ;

3) : ;

4) : .

Пусть  – одноместный предикат.

Высказывание  читается «для любого  имеет место ». Это высказывание истинно тогда и только тогда, когда предикат  при любых допустимых значениях переменной  превращается в истинное высказывание. Символ  называется квантором общности.

Высказывание  читается «существует  такое, что ». Это высказывание истинно тогда и только тогда, когда найдется такое допустимое значение переменной , при котором  будет истинным высказыванием. Символ  называется квантором существования.

Введенные кванторы применяются также к n -местным предикатам при . При этом получаются предикаты местности . Например, если  – двуместный предикат, то  – одноместный предикат от переменной .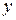

 

ПОНЯТИЕ МНОЖЕСТВА.