ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АВТОМАТОВ

 

Конечным детерминированным автоматом называется пятерка объектов , где  – конечные непустые множества соответственно состояний, входных и выходных сигналов, d – отображение множества  в множество S, называемое функцией переходов, а l – отображение множества  в множество Y, называемое функцией выходов.

Автомат A «работает» в дискретной временной шкале по следующему правилу: если  – состояние автомата A в данный момент времени и на его вход подан сигнал ,то в следующий момент времени автомат перейдет в состояние  и даст на выходе сигнал .

Полуавтоматом называется тройка объектов , где все символы несут тот же смысл, что и в определении автомата A.

Полуавтомат  называется редуктом автомата .

Автомат A может быть задан таблицей, состоящей из двух подтаблиц – переходов и выходов. Строки обеих таблиц помечаются элементами множества S, а столбцы – символами входного алфавита X. На пересечении строки s и столбца x в подтаблице переходов помещается элемент , а в подтаблице выходов – элемент .

Полуавтомат описывается только одной таблицей – таблицей переходов (отсутствует подтаблица, связанная с выходными сигналами).

Пример 2.1. Пусть задан автомат A, в котором ,  и функции d и l заданы следующей таблицей.

 

A	x1	x2	x1	x2
s1	s2	s1	0	1
s2	s3	s2	1	0
s3	s3	s2	1	0
s4	s4	s3	0	1

Из таблицы видно, например, что автомат A, находясь в состоянии , под воздействием сигнала  перейдет в состояние  и выдаст выходной сигнал 1.

Другим способом задания автомата является построение его диаграммы – графа с помеченными дугами. Вершины этого графа соответствуют состояниям автомата, и из вершины  в вершину  проводится дуга с метками 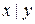, если 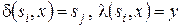. Например, диаграмма для автомата из примера 2.1 выглядит следующим образом:

Пусть ,  – произвольные автоматы. Гомоморфизм  (гомоморфизм автомата A₁ в автомат A₂) определяется как тройка отображений , , удовлетворяющих соотношениям

,

 для любых sÎS₁, xÎX₁.

Два автомата называются сравнимыми, если они имеют одинаковые множества входных сигналов и одинаковые множества выходных сигналов.

Пусть  и  – сравнимые автоматы. Отображение , по определению, является гомоморфизмом, если для любых  выполняются равенства

, .

Пример 2.2. Автомат A=(S,X,Y,d,l), где , ,  задан диаграммой

Автомат 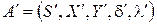, где , ,  задан диаграммой

 

 

 представляет собой гомоморфный образ автомата A. Тройка отображений  образует гомоморфизм автомата A на автомат .

Автомат  называется изоморфным автомату  (обозначение: ), если существует тройка взаимно однозначных соответствий  таких, что ,  для любых , .

Для сравнимых автоматов  и  изоморфизм автомата  на автомат  определяется как взаимно однозначное соответствие , удовлетворяющее равенствам ,  для любых , .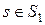

Изоморфные автоматы считаются разными копиями одного и того же абстрактного автомата.

Отношение изоморфности автоматов является отношением эквивалентности.

Обозначим через 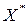 множество всех последовательностей конечной длины (слов), образованных из элементов множества X, называемого алфавитом. В множество  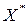включают и пустое слово e, не содержащее ни одной буквы.

Под длиной  слова  понимается количество содержащихся в p букв.

Функции переходов и выходов автомата 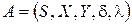 можно расширить на произвольные входные слова согласно индуктивным (по длине слов) формулам

,

.

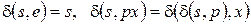Здесь  – произвольные элементы соответствующих множеств, а умножение в , которое присутствует в правой части четвертой формулы, понимается как приписывание к первому слову второго (операция конкатенации).

Индукцией по длине слова q легко доказываются следующие равенства:

, .

Значение продолженной функции переходов  определяет
состояние автомата, в которое он переходит из состояния s под воздействием входного слова p. Значение продолженной функции выходов  – это выходное слово, которое выдает автомат в результате указанного перехода.

Таким образом, автомат является моделью устройства, которое осуществляет некоторое отображение множества входных слов  в множество выходных слов .

Будем говорить, что состояние t достижимо из состояния s в автомате A, если существует входное слово , переводящее автомат A из состояния s в состояние t, т.е. если .

Каждое состояние достижимо из себя: d(s , e)=s. Состояния s и t взаимно достижимы в автомате A, если они достижимы друг из друга.

Отношение взаимной достижимости обозначим через . Таким образом,

.

 является отношением эквивалентности на множестве состояний автомата A. Классы этого отношения называются слоями автомата A.

Пример 2.3. Автомат задан диаграммой

 

 

Отношение взаимной достижимости  разбивает множество состояний автомата на два класса (три слоя автомата):

.

Пример 2.4. Выпишем значения продолженных функций перехода и выхода для автомата из примера 2.1, если автомат находится в состоянии s₁ и на вход подано слово .

,

,

,

;

,

,

,

,

.

Автомат называется сильно связным, если любые два его состояния взаимно достижимы, т.е. если  универсально на нем: .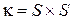

Пусть  – полуавтомат. Подмножество  называется устойчивым в A, если , т.е. когда никакими входными сигналами нельзя вывести полуавтомат из состояний класса .

В любом полуавтомате множество состояний S и его пустое подмножество Æ устойчивы.

Пусть  – устойчивое подмножество в полуавтомате . Полуавтомат  называется подавтоматом полуавтомата A, если  является ограничением функции d на множестве . В дальнейшем будем писать .

Каждый полуавтомат A имеет по крайней мере два подавтомата. Во-первых, сам полуавтомат A является своим подавтоматом, а во-вторых, подавтоматом будет и так называемый нулевой подавтомат O=(Æ,X,Æ) с пустыми множеством состояний и функцией переходов.

Ненулевые отличные от полуавтомата A его подавтоматы называются собственными. Совокупность всех подавтоматов полуавтомата A обозначается символом Sub A.

Если  и  – подавтоматы полуавтомата A, то положим

.

Очевидно, что введенное отношение £ является отношением порядка на множестве Sub A. Упорядоченное множество (Sub A,£) является решеткой (решетка подавтоматов полуавтомата A).

Действительно, упорядоченное множество (Sub A,£) имеет наибольший элемент (им является сам полуавтомат A) и для любых двух подавтоматов  и  существует наибольший содержащийся в них подавтомат, именно, .

Пример 2.5. Для автомата  из примера 2.3 редукт  будет иметь ту же диаграмму только без пометок на дугах выходными сигналами. Для 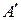 подмножества  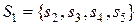и  – устойчивые и  и  – подавтоматы автомата .

Пусть  – некоторый полуавтомат. Эквивалентность q на множестве S называется конгруэнцией полуавтомата A, если она устойчива относительно функции переходов d в том смысле, что для любых состояний  и любого входного сигнала  выполняется условие

(т.е. если состояния  и  находятся в одном q-классе, то состояния, получаемые из них под действием входного сигнала x, тоже окажутся в одном q-классе).

В любом полуавтомате конгруэнциями будут тождественное отношение D и универсальное отношение .

Отношение взаимной достижимости состояний будет конгруэнцией в любом полуавтомате.

Совокупность всех конгруэнций полуавтомата A обозначим через Con A. Упорядоченное множество (Con A, Í) – есть решетка, так как пересечение  двух конгруэнций снова является конгруэнцией и  – тоже конгруэнция.

Пример 2.6. Полуавтомат , где ,   задан диаграммой

 

 

Устойчивыми относительно входного сигнала  будут разбиения

.

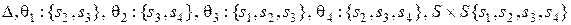(эквивалентности отождествляются с соответствующими разбиениями и указываются только неодноэлементные блоки).

Устойчивостью относительно  обладают разбиения

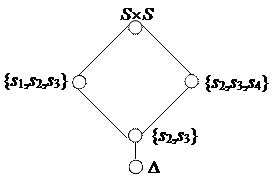и .

Диаграмма решетки Con A выглядит следующим образом:

Фактормножеством множества S по эквивалентности e будет множество , элементами которого являются всевозможные e-классы.

Отображение , сопоставляющее каждому элементу множества S класс отношения эквивалентности , содержащий этот элемент, называется естественным отображением множества S на фактормножество . Таким образом, .

Пусть  – некоторое отображение. Ядром его называют отношение

.

Другими словами, пара  входит в ядро Ker f тогда и только тогда, когда элементы  и  имеют один и тот же f-образ. Очевидно, что Ker f является эквивалентностью на множестве A.

Факторавтоматом полуавтомата A=(S,X,d) по конгруэнции q называется полуавтомат , где  для любых .

Пример 2.7. Ядром гомоморфизма 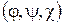 автомата A на автомат 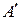, рассмотренного в примере 2.2, является конгруэнция q, состоящая из разбиения  множества S и тождественных отношений  и  (отображения y и c взаимно однозначны). Факторавтомат  представлен диаграммой

 

 

Факторавтомат  изоморфен автомату  (гомоморфному образу автомата A). Изоморфизм осуществляется соответствиями , , ; , ; .