 |
Главная |
ТАБЛИЧНОЕ И ЦЕПОЧНОЕ ЗАДАНИЕ ФУНКЦИЙ. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ
|
из
5.00
|
Пусть 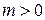 ,
,  – алфавит переменных, а
– алфавит переменных, а  – основное множество. Пусть
– основное множество. Пусть 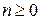 ,
,  , тогда
, тогда  называется множеством
называется множеством  -местных функций алгебры логики. Множество всех функций алгебры логики обозначается через
-местных функций алгебры логики. Множество всех функций алгебры логики обозначается через  .
.
Элементы множества  часто называют логическими функциями или булевыми функциями.
часто называют логическими функциями или булевыми функциями.
Пусть  , тогда
, тогда  и
и  ,
,  . Каждому элементу
. Каждому элементу  можно поставить во взаимно однозначное соответствие целое положительное число
можно поставить во взаимно однозначное соответствие целое положительное число  следующим образом:
следующим образом:
 .
.
Очевидно, что  . Это отмечено в 1.3.
. Это отмечено в 1.3.
Любая функция из 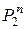 может быть задана с помощью таблицы, состоящей из
может быть задана с помощью таблицы, состоящей из 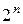 строк и двух столбцов. В строке i, где
строк и двух столбцов. В строке i, где 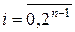 , в первом столбце записывается набор значений переменных
, в первом столбце записывается набор значений переменных  такой, что
такой, что  , а во втором столбце записывается значение функции
, а во втором столбце записывается значение функции  . Такое расположение элементов
. Такое расположение элементов  в таблице называется стандартным, а вся последовательность наборов – стандартной последовательностью наборов значений и обозначается через
в таблице называется стандартным, а вся последовательность наборов – стандартной последовательностью наборов значений и обозначается через 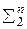 . Если значения функции, заданной на
. Если значения функции, заданной на 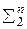 , записать в строку в виде цепочки элементов из
, записать в строку в виде цепочки элементов из 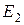 , то получим цепочку над
, то получим цепочку над  длины
длины 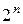 . Таким образом, функции из
. Таким образом, функции из 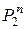 можно задавать не только в виде таблицы, но и в виде цепочки над
можно задавать не только в виде таблицы, но и в виде цепочки над  длины
длины 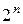 . Отсюда следует, что
. Отсюда следует, что 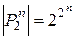 .
.
Пример 3.1. Пусть функция  задана таблицей.
задана таблицей.
(  , ,  ) )
| 
|
| (0,0) | 1 |
| (0,1) | 1 |
| (1,0) | 1 |
| (1,1) | 0 |
Тогда эта функция, заданная в виде цепочки, будет иметь вид  .
.
Функция  существенно зависит от переменной
существенно зависит от переменной  ,
,  , если существуют такие значения
, если существуют такие значения 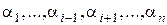 переменных
переменных  , что
, что

 .
.
При этом переменная 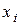 называется существенной. Переменные не являющиеся существенными называются фиктивными.
называется существенной. Переменные не являющиеся существенными называются фиктивными.
Пусть для функции 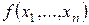 переменная
переменная 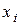 является фиктивной. В таблице для этой функции вычеркиваем все строки вида
является фиктивной. В таблице для этой функции вычеркиваем все строки вида  . Получим новую таблицу, которая будет определять некоторую функцию
. Получим новую таблицу, которая будет определять некоторую функцию 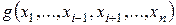 от
от  переменной. Говорят, что функция
переменной. Говорят, что функция  получена из функции
получена из функции  путем удаления фиктивной переменной
путем удаления фиктивной переменной 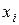 , а функция
, а функция  получена из функции
получена из функции  путем введения фиктивной переменной
путем введения фиктивной переменной  .
.
Функции 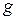 и
и  называется равными, если функцию
называется равными, если функцию 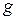 можно получить из функции
можно получить из функции  путем добавления или изъятия фиктивных переменных.
путем добавления или изъятия фиктивных переменных.
Пусть  , где
, где  ,
,  , и
, и  . Если к каждой функции
. Если к каждой функции  добавим
добавим  фиктивных переменных, то получим множество
фиктивных переменных, то получим множество  таких функций, что
таких функций, что  с точностью до фиктивных переменных.
с точностью до фиктивных переменных.
Обычно булевы функции при  называются простейшими или элементарными функциями. Рассмотрим элементарные функции, дадим им названия и приведем их обозначения.
называются простейшими или элементарными функциями. Рассмотрим элементарные функции, дадим им названия и приведем их обозначения.
Пусть 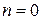 , тогда
, тогда  . В множестве
. В множестве 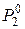 две функции, не зависящие от переменных. Это элементы множества
две функции, не зависящие от переменных. Это элементы множества 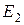 : константа
: константа 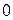 и константа
и константа  .
.
Пусть  , тогда
, тогда  . В множестве
. В множестве 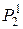 четыре функции, которые представлены в следующей таблице.
четыре функции, которые представлены в следующей таблице.
| Аргумент и функции | x | 
| 
| 
| 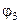
|
| Значения функций на наборах | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | |
| Обозначение функций | 0 | 
| x | 1 |
Названия:  – константа 0;
– константа 0;  – отрицание аргумента
– отрицание аргумента  , читается «не
, читается «не  »;
»;  – тождественная функция;
– тождественная функция;  – константа 1. Функции
– константа 1. Функции 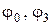 являются константами из
являются константами из  , так как переменная
, так как переменная  в них является фиктивной.
в них является фиктивной.
Пусть  , тогда
, тогда  . Функции из
. Функции из  представлены в следующей таблице.
представлены в следующей таблице.
(  ) )
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 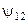
| 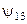
| 
| 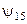
|
| (0,0) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| (0,1) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| (1,0) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| (1,1) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 
| 
| 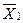
| 
| 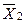
| 
| | | & | 
| 
| 
| 
| 
| 
| 1 |
В этой таблице содержатся функции, равные функциям из 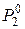 и
и 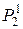 , когда одна или обе переменные являются фиктивными.
, когда одна или обе переменные являются фиктивными.
Функции  и
и 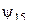 – это константы 0 и 1 соответственно и
– это константы 0 и 1 соответственно и 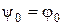 ,
, 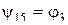 .
.
Функции  и
и  – функции одного переменного. Для них переменная
– функции одного переменного. Для них переменная  является фиктивной и
является фиктивной и  , а
, а  .
.
Функции  и
и  – функции одного переменного. Для них переменная
– функции одного переменного. Для них переменная  является фиктивной и
является фиктивной и 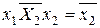 , а
, а  .
.
Все остальные функции не имеют фиктивных переменных.
Функция  называется стрелкой Пирса и обозначается
называется стрелкой Пирса и обозначается  .
.
Функция  не имеет названия и является отрицанием обратной импликации,
не имеет названия и является отрицанием обратной импликации,  и обозначается
и обозначается 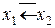 .
.
Функция 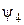 не имеет названия и является отрицанием импликации,
не имеет названия и является отрицанием импликации, 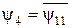 и обозначается
и обозначается  .
.
Функция  называется сложением
называется сложением  и
и  по модулю 2, обозначается
по модулю 2, обозначается  и читается «
и читается «  плюс
плюс  ».
».
Функция 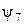 называется штрихом Шеффера и обозначается
называется штрихом Шеффера и обозначается  .
.
Функция  называется конъюнкцией, обозначается
называется конъюнкцией, обозначается  или
или  , или
, или  , или
, или  и читается «
и читается «  и
и  ».
».
Функция 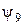 называется эквивалентностью, обозначается
называется эквивалентностью, обозначается  и читается «
и читается «  эквивалентно
эквивалентно  ».
».
Функция  называется импликацией, обозначается
называется импликацией, обозначается  или
или 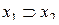 и читается «
и читается «  влечет
влечет  » или «
» или «  имплицирует
имплицирует  ».
».
Функция 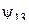 называется обратной импликацией, обозначается
называется обратной импликацией, обозначается  и читается «
и читается «  следует из
следует из  ».
».
Функция  называется дизъюнкцией, обозначается
называется дизъюнкцией, обозначается  или
или  и читается «
и читается «  или
или 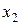 ».
».
При изучении функций было введено понятие суперпозиции функций. Суперпозицией функций над множеством (базисом) 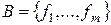 называется функция
называется функция  , полученная с помощью подстановок функций из множества
, полученная с помощью подстановок функций из множества 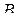 друг в друга и переименования имен переменных. Выражение, описывающее суперпозицию, называется формулой для функции
друг в друга и переименования имен переменных. Выражение, описывающее суперпозицию, называется формулой для функции  . Обычно формулы обозначаются большими латинскими буквами.
. Обычно формулы обозначаются большими латинскими буквами.
Пусть 
 и
и  .
.
1. Имена переменных будем называть формулами над 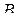 .
.
2. Пусть  ,
,  – формулы над
– формулы над 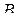 , тогда выражение
, тогда выражение  есть формула над
есть формула над  . Формулы
. Формулы  называются подформулами формулы
называются подформулами формулы  .
.
Очевидно, что любая формула 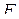 , выражающая функцию
, выражающая функцию  как суперпозицию функций из множества
как суперпозицию функций из множества  , задает способ ее вычисления при условии, что известны таблицы функций из множества
, задает способ ее вычисления при условии, что известны таблицы функций из множества  , входящих в формулу
, входящих в формулу 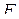 . Поэтому говорят, что формула
. Поэтому говорят, что формула  реализует функцию
реализует функцию  или, что функция
или, что функция  реализована формулой
реализована формулой 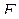 .
.
Пример 3.2. Пусть  . По определению формулы алгебры логики
. По определению формулы алгебры логики 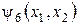 ,
,  и
и  являются формулами над множеством
являются формулами над множеством 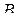 . В формуле
. В формуле 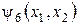 переименуем имена переменных. Вместо
переименуем имена переменных. Вместо 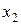 запишем
запишем 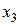 , а вместо
, а вместо  запишем
запишем  . Получим
. Получим 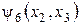 . Возьмем
. Возьмем  и подставим
и подставим  и
и 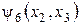 в
в  вместо
вместо  и
и  соответственно. Получим формулу
соответственно. Получим формулу  . В данной суперпозиции была использована префиксная запись функций. Для функций от двух переменных можно использовать инфиксную запись.
. В данной суперпозиции была использована префиксная запись функций. Для функций от двух переменных можно использовать инфиксную запись.
Тогда  . Используя обозначения для элементарных функций, получим
. Используя обозначения для элементарных функций, получим  . Так как таблицы функций
. Так как таблицы функций  ,
,  ,
, 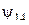 известны, то по формуле
известны, то по формуле 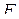 можно вычислить значение функции, реализованной этой формулой на любом наборе значений имен переменных. Вычислим
можно вычислить значение функции, реализованной этой формулой на любом наборе значений имен переменных. Вычислим  на наборе
на наборе  ,
,  ,
,  . Получим
. Получим  ,
,  ,
,  . Если формулу вычислить на всех
. Если формулу вычислить на всех 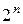 наборах, то можно получить таблицу функции, которую данная формула реализует. Следовательно, формула может служить еще одним способом задания функций.
наборах, то можно получить таблицу функции, которую данная формула реализует. Следовательно, формула может служить еще одним способом задания функций.
|
из
5.00
|
Обсуждение в статье: ТАБЛИЧНОЕ И ЦЕПОЧНОЕ ЗАДАНИЕ ФУНКЦИЙ. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

