РАЗЛОЖЕНИЕ БУЛЕВЫХ ФУНКЦИЙ ПО ПЕРЕМЕННЫМ. СОВЕРШЕННЫЕ ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ

 

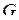Формулы  и 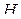, реализующие функци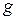и  и 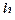 соответственно, называются эквивалентными, если .

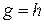Пример 3.3. Пусть 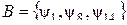, тогда 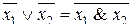. Каждая из этих формул реализует функцию , .

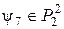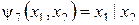Проблема эквивалентности формул 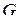 и 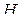 решается следующим образом. По формулам  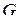и 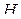 строятся таблицы функци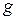й  и 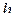. Если таблицы равны, то  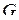и 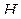 эквивалентны. Существуют и другие методы установления эквивалентности формул и получения новых формул, эквивалентных исходной.

При рассмотрении формул обозначения функций, из которых они построены, называются логическими или булевыми операциями, а имена переменных называются операндами. Рассмотрим основные свойства некоторых булевых операций, называемые иногда законами.

Коммутативность: 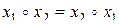, где .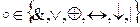

Ассоциативность: 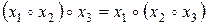, где .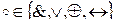

В следующих пяти законах 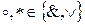 и .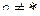

Дистрибутивность операции 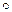 относительно операции *:

.

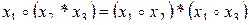Закон Де Моргана: .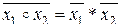

Закон поглощения: .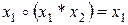

Закон склеивания: .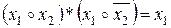

Идемпотентность: .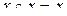

Двойное отрицание: .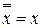

Закон противоречия: .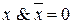

Закон «исключенного третьего» или закон тавтологии: .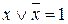

Исключение эквивалентности:

.

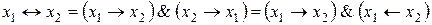Исключение импликации: .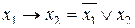

Законы для констант:

; ; ; ; , ; .

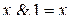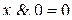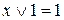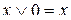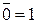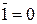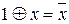Исключение сложения по : .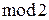

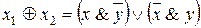Данные равенства легко проверить, построив таблицы функций для левой и правой частей равенства. Так как формулы не только являются символическими представлениями функций, но и реализуют их, то можно говорить и о значениях формул на любом наборе значений их операндов. Операнды формул принимают значение из 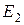 и значения формул принадлежат 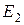, поэтому в любом равенстве для эквивалентных формул можно вместо всех вхождений любого операнда подставить какую-либо формулу, при этом равенство не нарушится. Данное правило подстановки формулы  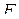вместо 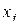, где 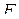– любая формула алгебры логики, а  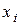– любой операнд равенства, позволяет получать новые равенства.

Пример 3.4. Пусть дано равенство

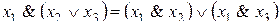
и формулы 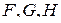, тогда верны следующие равенства:

;

;

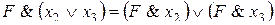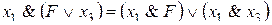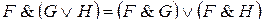, и так далее.

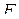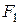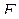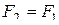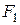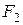Пусть  – какая-либо формула,  – подформула формулы  и . Так как  и  реализуют одну и ту же функцию, то  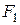в 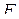 можно заменить на 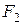, при этом получится новая формула  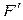реализующая ту же функцию, что и формула 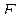, т.е. 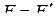. Данное правило замены позволяет получать формулы, эквивалентные исходной.

Пусть дана функция 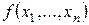. Функция  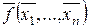называется двойственной к функции  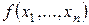и обозначается как .

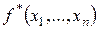Теорема 3.1. Пусть функция 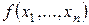 двойственна к функции 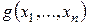. Тогда .

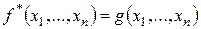Доказательство.

. „

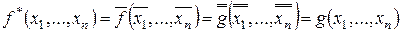Если 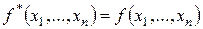, то функция  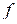называется самодвойственной.

Запишем двойственные функции для функций из 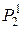 и .

; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .

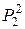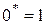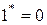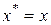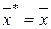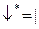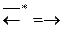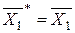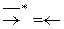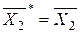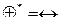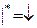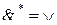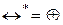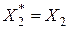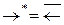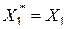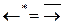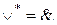Теорема 3.2.

Если 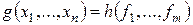, то .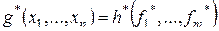

Доказательство.

. „

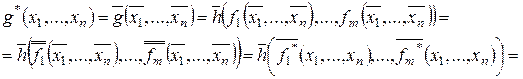
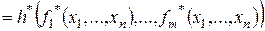Из этой теоремы следует утверждение, называемое принципом двойственности: пусть 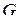 – формула, реализующая функцию 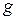; для получения формулы, реализующей функцию, двойственную к 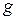, необходимо
в формуле 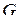 все знаки логических операций заменить на двойственные
к ним.

Принцип двойственности позволяет переходить от равенства 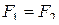 к равенству 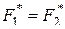, т.е. получать новые эквивалентные соотношения.

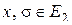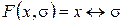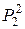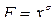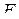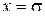
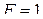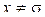
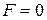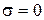
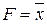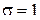
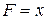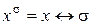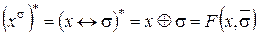Пусть . Возьмем функцию  из  и изменим ее обозначение на . По таблице для  имеем при , при , при , при . Так как , то . Поэтому .

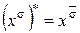Теорема 3.3. Любая булева функция 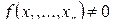 может быть представлена в виде

,

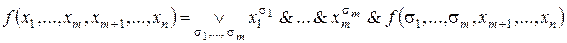где 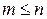, а дизъюнкция берется по всем  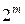наборам значений переменных .

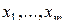Доказательство. Возьмем произвольный набор значений 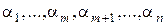 и подставим его в правую часть равенства, получим

.

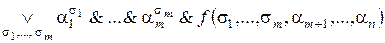Так как 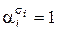 при 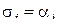, то из всех  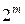конъюнкций  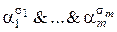только одна будет равна 1 – та, в которой 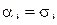, 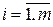. В результате получаем . „

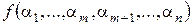Равенство, доказанное в теореме, называется разложением функции по 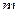 переменным .

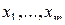Ясно, что аналогичное разложение справедливо для любого подмножества имен переменных, входящих в функцию.

Пример 3.5. Разложим функцию 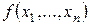 по переменной 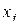, где .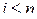

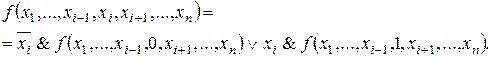
Пусть 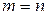. При этом все переменные в правой части формулы из теоремы 3.3 получают фиксированные значения, и функции в конъюнкциях становятся равными 0 или 1. Поэтому

,

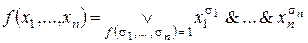где дизъюнкция берется по всем наборам 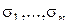, на которых .

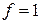Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции 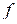. В СДНФ функции  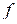каждому набору, на котором 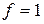, соответствует конъюнкция всех переменных, в которой  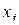взято с отрицанием, если 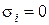, и без отрицания, если 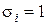. Таким образом, существует взаимно однозначное соответствие между функциями  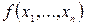и их СДНФ. Единственная функция, не имеющая СДНФ, – это константа 0.

Теорема 3.4. Любая булева функция может быть представлена булевой формулой над множеством .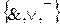

Доказательство. Любую функцию, кроме константы 0, можно представить в виде СДНФ. Константу 0 можно представить булевой формулой . „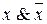

Пусть 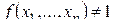, тогда очевидно, что 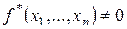. Поэтому

.

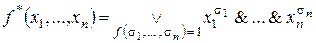Применим принцип двойственности к данной формуле, получим:

.

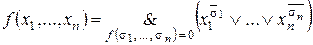Это выражение называется совершенной конъюнктивной нормальной формой (СКНФ) функции f.

 

ПОЛНОТА И ЗАМКНУТОСТЬ

 

Выше были рассмотрены два способа задания булевых функций – табличный и формульный. Таблицей функция задается как соответствие между n-наборами значений переменных и значениями функции на этих наборах. Любую функцию от 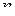 переменных из  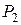можно задать таблицей, содержащей  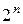строк. Формульный способ очень компактный, однако функция из  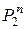при этом способе задается через другие функции, входящие в некоторый базис 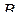, местность которых обычно не больше двух.

Множество функций 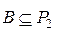 называется функционально полной системой, если любая булева функция может быть реализована формулой над 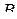, т.е. любую функцию из  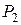можно представить в виде суперпозиции функций из .

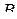Отметим, что множества 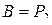 и 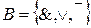 являются функционально полными системами.

Теорема 3.5 (о двух системах функций).

Пусть 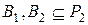, , 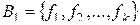 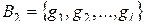и 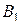 есть функционально полная система. Если любую функцию из  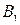можно представить в виде формулы над 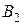, то множество функций  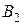является функционально полной системой.

Доказательство. Пусть 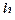 – произвольная функция из 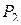. Из полноты системы  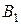следует, что  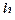можно выразить формулой над 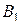. В формуле для  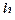все функции из  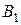выразим через функции из 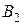. Получим, что любую функцию из  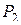можно выразить через функции системы 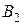. Отсюда следует, что 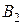– функционально полная система. „

Пример 3.6.

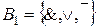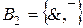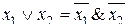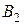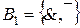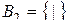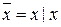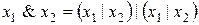Пусть , . Так как , то  – функционально полная система. Пусть , . Так как  и , то 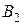– функционально полная
система.

Пусть 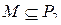. Замыканием множества  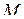называется множество всех функций, представимых в виде суперпозиций функций из 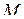. Обозначается замыкание через .

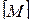Отметим некоторые свойства замыкания:

1) ,

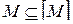2) ,

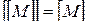3) если 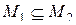, то ,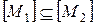

4) .

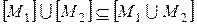Множество 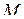 называется функционально замкнутым, если .

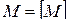Множество 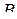 есть функционально полная система, если .

 

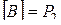Некоторые замкнутые классы из P ₂

 

Класс 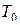.  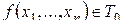тогда и только тогда, когда 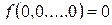. Таким образом,  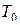– это класс функций, сохраняющих константу 0. Мощность этого класса .

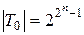Класс 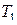.  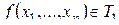тогда и только тогда, когда 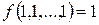. Таким образом,  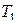– это класс функций, сохраняющих константу 1. Мощность этого класса 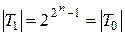, и .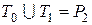

Класс 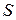.  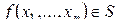тогда и только тогда, когда 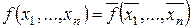. Мощность этого класса 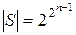. Он называется классом самодвойственных функций.

Класс 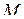. Пусть 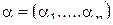,  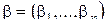и 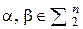. На множестве наборов значений переменных введем отношения порядка 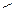, называемое отношением предшествования, следующим образом: 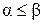, если , .

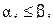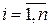Функция 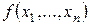 называется монотонной, если для любых  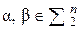таких, что 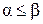, 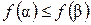. Класс  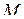– это класс монотонных функций.

Класс 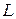. Функция  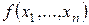называется линейной, если она представима в виде 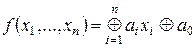. Класс  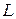называется классом линейных функций. Мощность этого класса .

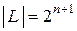Можно показать, что все перечисленные классы являются замкнутыми относительно суперпозиций, т.е. , , , , .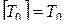

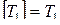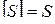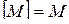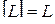ТЕОРЕМА 3.6 (о функции, не сохраняющей константу 0).

Если 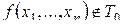, то из нее с помощью отождествления имен переменных можно получить либо константу 1, либо функцию .

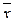ТЕОРЕМА 3.7 (о функции, не сохраняющей константу 1).

Если 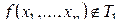, то из нее с помощью отождествления имен переменных можно получить либо константу 0, либо функцию .

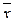ТЕОРЕМА 3.8 (о несамодвойственной функции).

Из несамодвойственной функции с помощью подстановк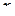и  или 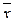 можно получить константы 0 или 1.

ТЕОРЕМА 3.9 (о немонотонной функции).

Из немонотонной функции с помощью подстановки констант можно получить функцию .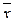

ТЕОРЕМА 3.10 (о нелинейной функции).

Из нелинейной функции с помощью подстановки констант и 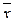 можно получить следующие функции: конъюнкцию 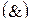, дизъюнкцию 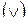, стрелку Пирса 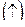, штрих Шеффера .

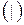ТЕОРЕМА 3.11 (о функциональной полноте).

Для того чтобы система функций 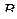 была функционально полной, необходимо и достаточно, чтобы она не содержалась ни в одном из пяти замкнутых классов , , , , .

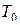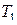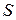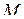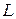Доказательство. Необходимость. Пусть 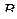 – функционально полная система функций и 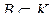, где 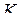 – один из указанных замкнутых классов. Тогда, так как 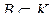, то 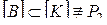. Что не верно, так как .

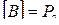Достаточность. Пусть 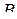 не содержится ни в одном из указанных замкнутых классов. Тогда в  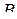найдутся функции, не принадлежащие ни одному из замкнутых классов. Согласно теоремам 3.6 – 3.10, с помощью этих функций можно построить отрицание и конъюнкцию, а так как  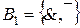– функционально полная система, то  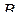– функционально полная система. „