 |
Главная |
МИНИМИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ
|
из
5.00
|
Состояния  автомата А называются неразличимыми (
автомата А называются неразличимыми (  или
или  ), если под воздействием любого входного слова
), если под воздействием любого входного слова  автомат А, находящийся в этих состояниях, выдаёт одинаковые выходные слова:
автомат А, находящийся в этих состояниях, выдаёт одинаковые выходные слова:  .
.
Если s и t не являются неразличимыми, то говорят, что они различимы и пишут s  t.
t.
e-неразличимость состояний в автомате есть отношение эквивалентности. Для построения e вводится понятие k-неразличимых состояний.
Состояния  называются k -неразличимыми (
называются k -неразличимыми (  или
или  ), если для любого входного слова
), если для любого входного слова  длины не более k при переходе из этих состояний выдаются одинаковые выходные слова
длины не более k при переходе из этих состояний выдаются одинаковые выходные слова
 .
.
При 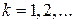 получается убывающая цепочка эквивалентностей
получается убывающая цепочка эквивалентностей  , каждая из которых содержит отношение e, так как если два состояния неразличимы, то они k-неразличимы при любом k. В силу конечности множества S будет конечно и множество
, каждая из которых содержит отношение e, так как если два состояния неразличимы, то они k-неразличимы при любом k. В силу конечности множества S будет конечно и множество 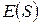 эквивалентностей на нём. Следовательно, указанная цепочка оборвётся на каком-то месте:
эквивалентностей на нём. Следовательно, указанная цепочка оборвётся на каком-то месте:  . По определению
. По определению
 ,
,  .
.
Понятие неразличимости состояний можно распространить на случай двух разных сравнимых автоматов. Если  – состояние автомата
– состояние автомата  , а
, а  – состояние автомата
– состояние автомата  , то полагаем:
, то полагаем:  .
.
Класс сравнимых автоматов  называется исключительным, если при
называется исключительным, если при  любое состояние автомата
любое состояние автомата  отличимо от любого состояния автомата
отличимо от любого состояния автомата 
Автомат А эквивалентен автомату В, если каждое состояние автомата А неразличимо с некоторым состоянием автомата В, и наоборот, каждое состояние автомата В неразличимо с некоторым состоянием автомата А.
О неэквивалентных автоматах говорят также, что они различимы. Содержательно эквивалентность двух автоматов А и В означает, что работу первого автомата А, начатую в любом из его состояний, может воспроизвести второй автомат В при соответствующем выборе его начального состояния, и наоборот. При этом внутренняя логика работы этих устройств может быть совершенно различной, существенным является лишь выдача одинаковых выходных слов на одни и те же входные слова. В этом существенное различие эквивалентности автоматов от их изоморфизма. Изоморфные сравнимые автоматы, очевидно, эквивалентны, но обратное в общем случае не верно.
Пример 2.8. Автоматы А и В заданы своими таблицами.
| B | x1 x2 | x1 x2 |
| t1 | t1 t2 | 0 1 |
| t2 | t2 t1 | 1 0 |
| А | x1 x2 | x1 x2 |
| s1 | s1 s2 | 0 1 |
| s2 | s3 s1 | 1 0 |
| s3 | s2 s1 | 1 0 |
Ясно, что  неразличимы в автомате А. Оба эти состояния неразличимы с
неразличимы в автомате А. Оба эти состояния неразличимы с  в автомате В, а
в автомате В, а  неразличимо с
неразличимо с  . Следовательно, автоматы А и В эквивалентны.
. Следовательно, автоматы А и В эквивалентны.
Теорема 2.1. Отношение неразличимости состояний в автомате  является конгруэнцией его редукта
является конгруэнцией его редукта  . ÿ
. ÿ
Признак эквивалентности сравнимых сильно связных автоматов. Пусть А и В – сильно связные сравнимые автоматы. Если в автомате А имеется хотя бы одно состояние, неразличимое с некоторым состоянием автомата В, то А и В – эквивалентны. „
Пусть 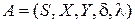 – некоторый автомат. Автомат с наименьшим возможным числом состояний среди автоматов, эквивалентных автомату А, называется минимальным автоматом в данном классе эквивалентных автоматов.
– некоторый автомат. Автомат с наименьшим возможным числом состояний среди автоматов, эквивалентных автомату А, называется минимальным автоматом в данном классе эквивалентных автоматов.
Очевидно, что автомат минимален тогда и только тогда, когда любые два его состояния различимы, т.е. когда отношение неразличимости состояний  тождественно на данном автомате.
тождественно на данном автомате.
Под конгруэнциями автомата  далее понимается конгруэнции его редукта
далее понимается конгруэнции его редукта  .
.
Теорема 2.2. Отношение неразличимости состояний  является наибольшей из конгруэнций автомата
является наибольшей из конгруэнций автомата  , содержащихся в отношении
, содержащихся в отношении
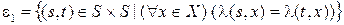 .
.
Доказательство. Само отношение  является конгруэнцией автомата А.
является конгруэнцией автомата А.
Пусть 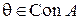 и
и  . Покажем, что
. Покажем, что  . Для этого достаточно установить, что
. Для этого достаточно установить, что  -конгруэнтные состояния автомата А не различимы входными словами никакой длины k. При
-конгруэнтные состояния автомата А не различимы входными словами никакой длины k. При  это следует из включения
это следует из включения  . Дальше действуем индукцией. Пусть
. Дальше действуем индукцией. Пусть  и
и  . Тогда для любого
. Тогда для любого  будет
будет  . Беря произвольное слово р длины k и произвольный входной сигнал
. Беря произвольное слово р длины k и произвольный входной сигнал  , получаем
, получаем
 , т.е.
, т.е.
 .
.
Таким образом  . „
. „
О конгруэнциях автомата, содержащихся в эквивалентности  , говорят, что они согласованы с функцией выходов.
, говорят, что они согласованы с функцией выходов.
Теорема 2.2 утверждает, что отношение неразличимости 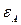 состояний автомата
состояний автомата  есть конгруэнция, согласованная с функцией выходов. Факторавтоматом автомата
есть конгруэнция, согласованная с функцией выходов. Факторавтоматом автомата  по конгруэнции
по конгруэнции 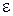 , согласованной с функцией выходов, называется автомат
, согласованной с функцией выходов, называется автомат  , где
, где  и
и  определены равенствами
определены равенствами
 ,
,
 ,
,
где  –
–  -класс состояния s.
-класс состояния s.
Теорема 2.3. Конгруэнция  автомата
автомата  тогда и только тогда является ядром некоторого гомоморфизма этого автомата, когда она согласована с функцией выходов l.
тогда и только тогда является ядром некоторого гомоморфизма этого автомата, когда она согласована с функцией выходов l.
Доказательство. Если j – гомоморфизм автомата А и  , т.е.
, т.е.  , то для любого
, то для любого 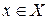 имеем
имеем
 , откуда
, откуда  .
.
С другой стороны, если 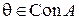 и
и  , то для любых
, то для любых
 -конгруэнтных состояний
-конгруэнтных состояний  будет
будет  при всех
при всех  . Значит, в факторавтомате
. Значит, в факторавтомате  имеем
имеем  для любых
для любых  ,
,  . Тогда естественное отображение
. Тогда естественное отображение  , оказывается гомоморфизмом автомата А на факторавтомат
, оказывается гомоморфизмом автомата А на факторавтомат  , причем
, причем
 . „
. „
СЛЕДСТВИЕ 2.1. Каждый автомат эквивалентен любому своему сравнимому гомоморфному образу.
Доказательство. Пусть j – гомоморфизм автомата  на сравнимый с A автомат
на сравнимый с A автомат  . Так как
. Так как  при любых
при любых  ,
,  , то для расширенной функции выходов имеем
, то для расширенной функции выходов имеем  , каковы бы ни были
, каковы бы ни были  ,
,  . Но это равенство означает, что состояние s автомата A неразличимо с состоянием
. Но это равенство означает, что состояние s автомата A неразличимо с состоянием  автомата B. В силу сюръективности отображения j каждое состояние автомата B имеет вид
автомата B. В силу сюръективности отображения j каждое состояние автомата B имеет вид  ,
,  , и поэтому неразличимо с соответствующим состоянием s автомата A. „
, и поэтому неразличимо с соответствующим состоянием s автомата A. „
СЛЕДСТВИЕ 2.2. Каждый автомат эквивалентен своему факторавтомату по отношению неразличимости состояний:  .. „
.. „
Следующая лемма и следствие из нее устанавливают некоторые свойства решетки эквивалентностей на конечном множестве.
Лемма 2.1. В решетке  разбиений n-элементного множества высота элемента
разбиений n-элементного множества высота элемента  может быть вычислена по формуле
может быть вычислена по формуле  , где
, где  – число блоков разбиения
– число блоков разбиения  .
.
Доказательство. Действуем индукцией по n. Для  утверждение очевидно. Пусть доказываемое утверждение справедливо при
утверждение очевидно. Пусть доказываемое утверждение справедливо при  . Рассмотрим решетку
. Рассмотрим решетку  разбиений множества
разбиений множества  . Каждое разбиение
. Каждое разбиение 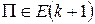 получается из некоторого однозначно определенного разбиения
получается из некоторого однозначно определенного разбиения  одним из двух способов: 1) присоединением одноэлементного блока
одним из двух способов: 1) присоединением одноэлементного блока  , 2) добавлением в один из
, 2) добавлением в один из  -блоков элемента
-блоков элемента  . В первом случае, очевидно,
. В первом случае, очевидно,  (высоты вычисляются в соответствующих решетках), а во втором
(высоты вычисляются в соответствующих решетках), а во втором  . В обеих ситуациях
. В обеих ситуациях  . „
. „
Длиной конечного упорядоченного множества называется наибольшая из высот его элементов, т.е. наибольшая из длин его цепей.
СЛЕДСТВИЕ 2.3. Решетка  разбиений n-элементного множества имеет длину
разбиений n-элементного множества имеет длину  .
.
Доказательство. Наибольшим элементом решетки  является разбиение, соответствующее универсальной эквивалентности. Оно имеет один блок и потому, согласно лемме, его высота равна
является разбиение, соответствующее универсальной эквивалентности. Оно имеет один блок и потому, согласно лемме, его высота равна  . Это число и будет длиной решетки
. Это число и будет длиной решетки  .
.
Теорема 2.4 (Мур). Для автомата с n состояниями  .
.
Доказательство. Поскольку цепь  составлена из эквивалентностей на n-элементном множестве, длина ее, ввиду предыдущего следствия, не может быть больше, чем
составлена из эквивалентностей на n-элементном множестве, длина ее, ввиду предыдущего следствия, не может быть больше, чем  . „
. „
Теорема Мура утверждает, что если в автомате с n состояниями состояния s и t не различимы входными последовательностями длины, не превосходящей  , то эти состояния не различимы никакими входными последовательностями.
, то эти состояния не различимы никакими входными последовательностями.
Теорема 2.5. В каждом классе сравнимых эквивалентных автоматов существует единственный с точностью до изоморфизма минимальный автомат, который может быть получен по формуле  , где А – произвольный автомат из класса сравнимых эквивалентных автоматов,
, где А – произвольный автомат из класса сравнимых эквивалентных автоматов, 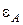 – от ношение неразличимости состояний автомата А.
– от ношение неразличимости состояний автомата А.
Методы минимизации автоматов сводятся к построению отношения неразличимости состояний e в данном автомате A и последующей факторизации автомата A по конгруэнции e. Отношение  легко определяется по таблице, задающей автомат. Если решетка конгруэнций автомата A известна, то в ней без труда выделяется наибольшая из конгруэнций, содержащихся в
легко определяется по таблице, задающей автомат. Если решетка конгруэнций автомата A известна, то в ней без труда выделяется наибольшая из конгруэнций, содержащихся в  . Это и будет e.
. Это и будет e.
Если Con A не известна, то e (отношение неразличимости) легко получить следующим образом.
Сначала строятся  -классы состояний (по таблице автомата). Состояния
-классы состояний (по таблице автомата). Состояния 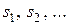 попадают в один
попадают в один  -класс, если выходные сигналы
-класс, если выходные сигналы  ,
,  , … совпадают при любом выборе входного сигнала x.
, … совпадают при любом выборе входного сигнала x.
 -классы разбиваются на
-классы разбиваются на  -классы: состояния
-классы: состояния  , содержащиеся в одном и том же
, содержащиеся в одном и том же  -классе, объединяются в один и тот же
-классе, объединяются в один и тот же  -класс, если при любом выборе входного сигнала x состояния
-класс, если при любом выборе входного сигнала x состояния  ,
,  , … содержатся в одном и том же
, … содержатся в одном и том же  -классе, зависящим от выбора x, но не зависящим от выбора состояний
-классе, зависящим от выбора x, но не зависящим от выбора состояний 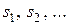 в
в  -классе.
-классе.
Затем разбиваются  -классы аналогичным образом на
-классы аналогичным образом на  -классы и т.д. В случае конечных автоматов через конечное число шагов для некоторого
-классы и т.д. В случае конечных автоматов через конечное число шагов для некоторого 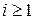
 -классы совпадут с
-классы совпадут с  -классами. Эти
-классами. Эти  -классы и будут искомыми e-классами отношения e.
-классы и будут искомыми e-классами отношения e.
Факторавтомат  и будет минимальным автоматом в классе автоматов, эквивалентных автомату A.
и будет минимальным автоматом в классе автоматов, эквивалентных автомату A.
Пример 2.9. В автомате A из примера 2.1 отношение 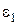 имеет своими классами подмножества
имеет своими классами подмножества  (в подтаблице выходов совпадают строки 1 и 4, а также 2 и 3). Решетка конгруэнций автомата A (пример 2.6) содержит 5 элементов. Наибольшей конгруэнцией, включающейся в отношение
(в подтаблице выходов совпадают строки 1 и 4, а также 2 и 3). Решетка конгруэнций автомата A (пример 2.6) содержит 5 элементов. Наибольшей конгруэнцией, включающейся в отношение 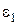 , будет
, будет  . Следовательно,
. Следовательно, 
и минимальный автомат  можно задать диаграммой из примера 2.7
можно задать диаграммой из примера 2.7
(с учетом пометок выходных сигналов).
Пример 2.10. Автомат A задан таблицей.
| A | x1 x2 | x1 x2 |
| 1 | 2 8 | 0 0 |
| 2 | 5 3 | 0 1 |
| 3 | 4 6 | 0 0 |
| 4 | 7 1 | 0 1 |
| 5 | 1 8 | 0 0 |
| 6 | 5 2 | 1 1 |
| 7 | 3 6 | 0 0 |
| 8 | 7 4 | 1 1 |
Непосредственно из таблицы находим отношение  (оно состоит из трех классов
(оно состоит из трех классов 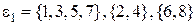 ).
).  -класс
-класс  не расщепляется на
не расщепляется на
 -классы, так как по сигналу
-классы, так как по сигналу  состояния 2 и 4 соответственно переходят в состояния 5 и 7, которые принадлежат одному
состояния 2 и 4 соответственно переходят в состояния 5 и 7, которые принадлежат одному  -классу, и по сигналу
-классу, и по сигналу  переходят в 3 и 1, которые также принадлежат одному
переходят в 3 и 1, которые также принадлежат одному  -классу. Аналогично не расщепляется на
-классу. Аналогично не расщепляется на  -классы и
-классы и  . Класс
. Класс  расщепляется на два
расщепляется на два  -класса
-класса  ,
, 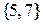 , которые далее уже не дают новых
, которые далее уже не дают новых  -классов. Не дают новых классов и
-классов. Не дают новых классов и  ,
,  . Таким образом,
. Таким образом,  ,
,  . Факторавтомат
. Факторавтомат  , где
, где  ,
,  ,
,  ,
, 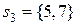 ,
,  задается следующей таблицей.
задается следующей таблицей.
| A | x1 x2 | x1 x2 |
| s1 | s2 s4 | 0 0 |
| s2 | s3 s1 | 0 1 |
| s3 | s1 s4 | 0 0 |
| s4 | s3 s2 | 1 1 |
Пример 2.11. Автомат A задан таблицей.
| A | x1 x2 x3 | x1 x2 x3 |
| 1 | 2 2 5 | 1 0 0 |
| 2 | 1 4 4 | 0 1 1 |
| 3 | 2 2 5 | 1 0 0 |
| 4 | 3 2 2 | 0 1 1 |
| 5 | 6 4 3 | 1 0 0 |
| 6 | 8 9 6 | 0 1 1 |
| 7 | 6 2 8 | 1 0 0 |
| 8 | 4 4 7 | 1 0 0 |
| 9 | 7 9 7 | 0 1 1 |
Выпишем классы отношений  ,
,  , и т.д.
, и т.д.
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Так как  , то
, то  и в таблице, задающей факторавтомат
и в таблице, задающей факторавтомат  (минимальный автомат),
(минимальный автомат),  .
.
| A/e | x1 x2 x3 | x1 x2 x3 |
| s1 s2 s3 s4 s5 | s2 s2 s3 s1 s2 s2 s4 s2 s1 s1 s5 s4 s3 s5 s3 | 1 0 0 0 1 1 1 0 0 0 1 1 0 1 1 |
Глава 3. Алгебра логики
|
из
5.00
|
Обсуждение в статье: МИНИМИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

