Отношения эквивалентности и разбиения множеств

Пусть Æ. Отношение  называется отношением эквивалентности (кратко: эквивалентностью) на множестве A, если оно рефлексивно, симметрично и транзитивно.

Из определения следует, что e будет эквивалентностью тогда и только тогда, когда e транзитивно и является толерантностью.

Пример 1.13.

1. Отношение  из пункта 1 в примере 1.12 не будет транзитивным при любом 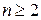 (при 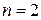 отсутствие свойства транзитивности у t хорошо «видно» на приведенном рисунке графа 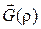). Следовательно, при  отношение t не будет эквивалентностью. При  отношение t={((0),(0)),((1),(1))} является эквивалентностью на .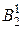

2. Отношение º_k из пункта 2 примера 1.12 транзитивно и, следовательно, является эквивалентностью на N (при любом kÎN).

3. Диагональ D_A на произвольном множестве Æ является эквивалентностью.

4. Универсальное отношение 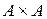 также является эквивалентностью на любом множестве Æ.

5. Пусть L – множество всех прямых на плоскости. Рассмотрим отношение || на L, где l₁||l₂ означает, что прямая l₁ параллельна прямой l₂. Отношение || является отношением эквивалентности на L.

6. На множестве R введем отношение l, положив 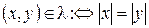 для произвольных . Отношение l – эквивалентность на R.

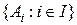Пусть Æ. Совокупность A =  непустых подмножеств множества A называется разбиением множества A, если выполнены следующие условия:

1) ;

2) .

Множества , называются блоками разбиения А.

Пусть  – эквивалентность на множестве Æ, 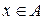. Множество  называется e-классом элемента х.

Теорема 1.8 (основная теорема об эквивалентностях). Пусть 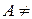Æ.

1. Каждому отношению эквивалентности e на множестве A соответствует разбиение A ={e(х)| хÎA } этого множества.

2. Каждому разбиению A множества A соответствует эквивалентность

e(A):={(x,y)ÎA´A| “х находится в одном блоке разбиения A с y”} на множестве A.

3. Указанные соответствия взаимно однозначны и взаимно обратны в том смысле, что e(A(e))=e, A(e(A))=A.ÿ

Пусть A¹Æ, e – эквивалентность на A. Разбиение A(e), о котором говорилось в теореме 1.8, называется фактормножеством множества A по эквивалентности e и обозначается A/e.

Пример 1.14.

1. Рассмотрим эквивалентность º_k на N при различных kÎN. Имеем:

а) N/º₁={{1,2,3,…}}, так как все натуральные числа при делении на 1 дают один и тот же остаток 0;

б) N/º₂={{1,3,5,7,…}, {2,4,6,8,…}}, так как все нечетные числа при делении на 2 дают один и тот же остаток 1, а все четные числа – остаток 0;

в) N/º₃={{1,4,7,10,…}, {2,5,8,11,…}, {3,6,9,12,…}}.

2. Если Æ, то A/D_A={{a}|aÎA} (все D_A -классы одноэлементны).

3. Если Æ, то A/A´A={A} (фактормножество множества A по универсальному отношению 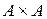 состоит из одного блока – самого множества A).

4. Для эквивалентности l={(x,y)ÎR´R:|x|=|y|} имеем

R/l={{0}}È{{x,- x}|x>0}.