 |
Главная |
Арифметические операции над
|
из
5.00
|
Действительными числами
Пусть а=а0,а1а2…an… - произвольное действительное число. Пусть для определенности a > 0. Оборвем дробь на k - ом знаке после запятой. Получим рациональное число а0,а1а2…ak . Увеличив его на 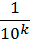 , получим другое рациональное число а0,а1а2…ak +
, получим другое рациональное число а0,а1а2…ak + 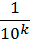 . По правилу сравнение действительных чисел имеем а0,а1а2…ak ≤ а0,а1а2…ak… ≤ а0,а1а2…ak +
. По правилу сравнение действительных чисел имеем а0,а1а2…ak ≤ а0,а1а2…ak… ≤ а0,а1а2…ak + 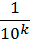 ,
, 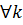 . При увеличении k дробь
. При увеличении k дробь 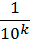 может быть сделана как угодно малой. Значит, для любого действительного числа а и любого как угодно малого числа ε < 0 найдутся рациональные числа α1 и α2 такие, что α1 ≤ α ≤ α2. α2 - α1 < ε.
может быть сделана как угодно малой. Значит, для любого действительного числа а и любого как угодно малого числа ε < 0 найдутся рациональные числа α1 и α2 такие, что α1 ≤ α ≤ α2. α2 - α1 < ε.
Пусть а и b – действительные числа, α1 ≤ а ≤ α2, β1 ≤ b ≤ β2, где α1 и α2, β1 и β2 – рациональные числа, построенные как выше.
Определение 1. Суммой действительных чисел а и в назовем действительное число с, удовлетворяющим неравенствам α1+ β1 ≤ с ≤ α2+ β2.
Можно показать, что такое число с существует и единственно. Нетрудно догадаться, что этим числом является верхняя грань множества всех сумм α1+ β1. Это множество не пусто и ограничено сверху, т.е. имеет верхнюю грань. Она совпадает с нижней гранью множества всех сумм α2+ β2.
Определение 2. Разностью а – b действительных чисел а и b назовем действительное число r такое, что b + r = a.
Определение 3. Произведением положительных действительных чисел а и b назовем такое действительное число p, что α1β1 ≤ p ≤ α2β2.
Произведение действительных чисел любого вида определяется по правилу:
1) а∙0 = 0∙а = 0
2) Если а и b одного знака, то а∙b > 0, если а и b разных знаков, то а∙b < 0.
Определение 4. Частным  (b≠0) действительных чисел а и b называется число l такое, что b∙l = a.
(b≠0) действительных чисел а и b называется число l такое, что b∙l = a.
Неравенство Бернулли.
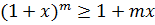 (m – натуральное число, х – действительное число, х>-1).
(m – натуральное число, х – действительное число, х>-1).
Доказательство методом математической индукции.
m = 1. Соотношение справедливо: 1+x = 1+ x.
m = k. Допустим, что справедливо
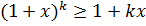 . (1)
. (1)
m = k+1. Умножим обе части неравенства (1) на 1+x >0.
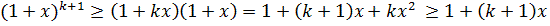
То есть неравенство справедливо при любом натуральном k.
Абсолютная величина действительного числа
Число, обозначаемое через 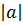 и определенное для любого действительного числа a по формуле
и определенное для любого действительного числа a по формуле 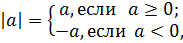 называется абсолютной величиной числа a.
называется абсолютной величиной числа a.
Теорема 1. Неравенства 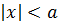 и –a<x<a равносильны.
и –a<x<a равносильны.
Доказательство. 1) Дано 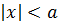 , т.е.
, т.е.  ,
, 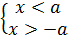 , –a< x < a.
, –a< x < a.
2)Дано –a < x < a. Значит 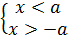 ,
,  .
.
Одно из чисел x или (-x) есть 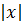 . Значит
. Значит 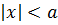 . Теорема доказана.
. Теорема доказана.
Теорема 2. 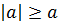 ,
, 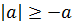 .
.
Доказательство. Если a ≥ 0, то 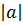 = a. Значит –a ≤ 0 ≤ a =
= a. Значит –a ≤ 0 ≤ a = 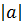 . Если a < 0, то a < 0 < - a =
. Если a < 0, то a < 0 < - a = 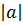 . Теорема доказана.
. Теорема доказана.
Из теорем 2 и 1 можно записать – 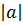 ≤ a ≤
≤ a ≤ 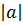
Теорема 3. 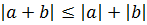 ,
, 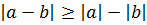 .
.
Доказательство. 1) – 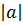 ≤ a ≤
≤ a ≤ 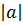 , –
, – 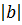 ≤ b ≤
≤ b ≤ 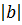 . Сложив эти неравенства, имеем
. Сложив эти неравенства, имеем  и по теореме 1
и по теореме 1 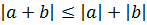 . 2) a=(a-b)+b.
. 2) a=(a-b)+b.  , т.е.
, т.е. 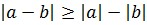 . Теорема доказана.
. Теорема доказана.
Теорема 4. 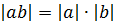 ,
, 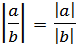 .
.
Доказательство следует из правил умножения и деления действительных чисел.
Промежутки
Множество  , состоящее из множества R действительных и двух символов, или точек, - ∞ и + ∞, называется расширенным множеством действительных чисел. На символы - ∞ и + ∞ распространяется отношение порядка по правилу - ∞ < x, + ∞ > x, - ∞ < + ∞,
, состоящее из множества R действительных и двух символов, или точек, - ∞ и + ∞, называется расширенным множеством действительных чисел. На символы - ∞ и + ∞ распространяется отношение порядка по правилу - ∞ < x, + ∞ > x, - ∞ < + ∞, 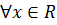 .
.
Обычные действительные числа в отличии от - ∞ и + ∞ называются конечными действительными числами. По определению x + (+ ∞) = + ∞, x + (- ∞) = - ∞, 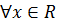 ; (+∞) + ( - ∞) не имеет смысла. Для
; (+∞) + ( - ∞) не имеет смысла. Для 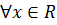 , x > 0 x ∙ (+ ∞) = + ∞, x ∙ (- ∞) = - ∞, (- x) ∙ (+∞) = - ∞, ( - x) ∙ ( - ∞) = + ∞, ( + ∞) ∙ (+ ∞) = + ∞, (- ∞) ∙ ( - ∞) = + ∞, (+ ∞) ∙ ( - ∞) = - ∞. Не определено 0∙( + ∞) и 0 ∙ ( - ∞).
, x > 0 x ∙ (+ ∞) = + ∞, x ∙ (- ∞) = - ∞, (- x) ∙ (+∞) = - ∞, ( - x) ∙ ( - ∞) = + ∞, ( + ∞) ∙ (+ ∞) = + ∞, (- ∞) ∙ ( - ∞) = + ∞, (+ ∞) ∙ ( - ∞) = - ∞. Не определено 0∙( + ∞) и 0 ∙ ( - ∞).
Множества действительных чисел, называемые промежутками, имеют специальные обозначения.
| Удовлетворяет условиям | Обозначается | Называется | Изображается | |||
| a ≤ x ≤ b | [a,b] | Сегмент, отрезок, замкнутый промежуток. |
a b
| |||
| a < x < b | (a,b) | Интервал, открытый промежуток. |
  a b
a b
  a b
a b
| |||
| a ≤ x <b | [a,b) | Полуинтервал. |    a b
a b
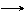   a b
a b
| |||
| a ≤ x a ≥ x | [a, + ∞) ( - ∞, a] | Полупрямая, луч. |   A
A
| |||
| a >x a < x | (- ∞,a) (a, + ∞) | Открытая полупрямая. |  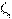 A
A
| |||
| Множество всех дейст. чисел. | ( - ∞, +∞) | Прямая. |
Например, множество M = {x ϵ R, a ≤ x < b} = [a,b).
Для заданного x всякий интервал вида, (x - ε, x+ε), где ε > 0, называется ε – окрестностью или просто окрестностью числа x на числовой прямой.
Глава 2. Функции
|
из
5.00
|
Обсуждение в статье: Арифметические операции над |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


