 |
Главная |
Верхняя и нижняя грани числового множества
|
из
5.00
|
Определение 1. Множество М действительных чисел называется ограниченным сверху (снизу), если существуют такое действительное число а, что для всякого 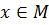 выполняется неравенство
выполняется неравенство 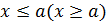 . Число а ограничивает множество М сверху (снизу) и называется верхней (нижней) границей множества М.
. Число а ограничивает множество М сверху (снизу) и называется верхней (нижней) границей множества М.
Определение 2. Множество, ограниченное сверху и снизу, называется ограниченным множеством.
Пример. Множество натуральных чисел ограничено снизу, но ограниченным не является. Множество корней уравнения х2 – 4=0 ограничено.
Если множество не является ограниченным (сверху, снизу), то оно называется неограниченным (сверху, снизу).
Если множество М ограниченно сверху, то оно имеет бесконечно много верхних границ, т.к. если а- верхняя граница, то любое b >а тоже является верхней границей.
Определение 3. Наименьшее из верхних границ ограниченного сверху множества называется точной верхней границей или верхней гранью. Пишут sup M или 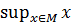 (supremum (лат) – наивысшее).
(supremum (лат) – наивысшее).
Пример. М - множество отрицательных целых чисел, 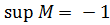 . М={x:1≤ x <2}. sup M = 2.
. М={x:1≤ x <2}. sup M = 2.
Верхняя грань может принадлежать самому множеству М, а может и не принадлежать ему.
Если существует такой элемент 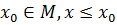 ,
, 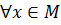 , то
, то 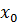 называется наибольшим или максимальным элементом множества М. Пишут
называется наибольшим или максимальным элементом множества М. Пишут 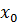 =max M. Если в множестве М имеется наибольший элемент
=max M. Если в множестве М имеется наибольший элемент 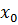 , то sup M =
, то sup M = 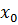 .
.
Определение 3. Наибольшая из нижних границ ограниченного снизу множества М называется точной нижней границей или нижней гранью множества М. Пишут inf M или 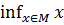 . (infimum (лат.) - наинизшее).
. (infimum (лат.) - наинизшее).
Еслисуществуетэлемент 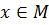 такой, что
такой, что 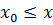 ,
, 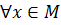 , то
, то 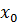 называется наименьшим элементом множества М. пишут
называется наименьшим элементом множества М. пишут 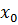 = min M. В этом случае inf M =
= min M. В этом случае inf M = 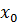 .
.
Теорема 1. Если непустое множество М действительных чисел ограничено сверху, то оно имеет верхнюю грань.
Доказательство. Так как множество М ограничено сверху, то существует действительное число а такое, что 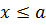 ,
, 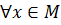 . Возможны два случая.
. Возможны два случая.
1)Множество М содержит хотя бы одно неотрицательное число.
2)Все элементы множества М отрицательны.
Сначала рассмотрим случай. 1). Отделим все неотрицательные числа и каждое из них представим в виде бесконечной десятичной дроби. Так как все эти числа ≤ а, то среди этих целых частей найдется наибольшая. Обозначим ее через 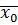 .
.
Сохраним только те числа из М, у которых целая часть равна 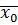 . У этих чисел рассмотрим первые десятичные знаки. Наибольший из них обозначим через
. У этих чисел рассмотрим первые десятичные знаки. Наибольший из них обозначим через 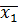 и т. д. Продолжая этот процесс неограниченно, получим действительное число
и т. д. Продолжая этот процесс неограниченно, получим действительное число 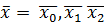 …
… 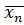 … Покажем, что
… Покажем, что 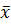 – верхняя грань множества М. Для этого нужно доказать: а)
– верхняя грань множества М. Для этого нужно доказать: а) 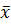 – верхняя граница, т. е.
– верхняя граница, т. е. 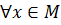 будет
будет 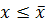 ; b)
; b) 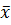 - наименьшая из верхних границ. Это доказать можно так: если
- наименьшая из верхних границ. Это доказать можно так: если 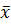 - наименьшая из верхних границ, то если взять любое действительное число
- наименьшая из верхних границ, то если взять любое действительное число 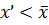 , то найдется
, то найдется 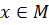 , x
, x 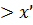 .
.
Итак, сначала докажем, что 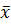 - верхняя граница. Ясно, что
- верхняя граница. Ясно, что 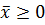 . Поэтому для любого отрицательного числа
. Поэтому для любого отрицательного числа 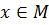 будет x<
будет x< 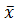 . Пусть х – произвольное отрицательное число из М, x
. Пусть х – произвольное отрицательное число из М, x 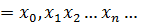
По построению 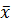 имеем
имеем 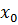 ≤
≤ 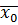 . Если
. Если 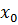 <
< 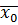 , то x<
, то x< 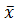 и
и 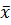 - верхняя граница. Если
- верхняя граница. Если 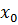 =
= 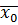 , то по построению
, то по построению 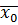 имеем x1 ≤
имеем x1 ≤ 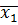 . Если здесь x1 <
. Если здесь x1 < 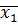 , то x<
, то x< 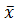 , т. е.
, т. е. 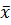 - верхняя граница.
- верхняя граница.
Продолжая этот процесс неограниченно, получим либо x< 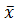 , либо бесконечное множество равенств
, либо бесконечное множество равенств 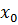 =
= 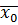 , x1 =
, x1 = 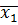 , … , xn =
, … , xn = 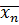 ,… В этом случае х =
,… В этом случае х = 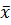 , т. е. и здесь
, т. е. и здесь 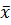 - верхняя граница.
- верхняя граница.
Осталось доказать, что 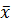 - наименьшая из верхних границ. Возьмем произвольное действительное число х' <
- наименьшая из верхних границ. Возьмем произвольное действительное число х' < 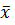 , х' = х'0, x'1x'2… x'n … Т. к. х' <
, х' = х'0, x'1x'2… x'n … Т. к. х' < 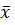 , то найдется номер k такой, что
, то найдется номер k такой, что
х'0 = 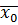 , x'1=
, x'1= 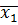 … x'k-1=
… x'k-1= 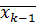 , x'k <
, x'k < 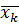 . (1)
. (1)
С другой стороны, число 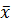 строилась так, что среди элементов множества М найдется число х=х0, x1 х2… xn… такое, что
строилась так, что среди элементов множества М найдется число х=х0, x1 х2… xn… такое, что
х0 = 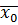 , x1=
, x1= 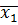 … xk-1=
… xk-1= 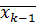 , xk =
, xk = 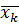 . (2)
. (2)
Сопоставив (1) и (2), имеем х>х', 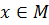 . Таким образом
. Таким образом 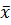 - верхняя грань.
- верхняя грань.
Случай 2), когда все элементы множества М отрицательны. Метод доказательства остается тот же. Число 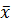 строим так:
строим так: 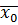 - наименьшая из целых частей (без знака),
- наименьшая из целых частей (без знака), 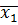 – наименьший из первых десятичных знаков и т.д. Получим отрицательное действительное число
– наименьший из первых десятичных знаков и т.д. Получим отрицательное действительное число 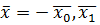 …
… 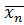 … Аналогично 1) доказываем, что
… Аналогично 1) доказываем, что 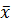 =supM. Теорема доказана.
=supM. Теорема доказана.
Теорема 2. Если непустое множество M действительных чисел ограничено снизу, то оно имеет нижнюю грань. (Доказательство аналогично).
Следствие. Всякое непустое ограниченное множество действительных чисел имеет верхнюю и нижнюю грани.
Если множество M неограниченно сверху (снизу), то никакое действительное число не может являться верхней (нижней) гранью. По определению полагаем supM=+∞ (infM= -∞).
Пример. 1) M = {1, 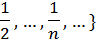 . supM = max M =1. inf M = 0. 0 ∉ М,
. supM = max M =1. inf M = 0. 0 ∉ М, 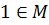 .
.
2) М = {1,2,…,n,…}. supM =+∞. infM = minM =1. 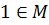 .
.
|
из
5.00
|
Обсуждение в статье: Верхняя и нижняя грани числового множества |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

