 |
Главная |
Свойства функции, имеющей предел
|
из
5.00
|
Теорема 1. Если  и A < C, то существует окрестность точки x0 такая, что во всех точках этой окрестности, кроме, быть может, самой токи x0, выполняется неравенство
и A < C, то существует окрестность точки x0 такая, что во всех точках этой окрестности, кроме, быть может, самой токи x0, выполняется неравенство  .
.
Доказательство. Возьмем ε = C – A. Так как  , то
, то 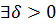 такое, что при
такое, что при  выполняется
выполняется 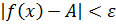 , т.е.
, т.е.  . Теорема доказана.
. Теорема доказана.
Теорема 2. Если  и A > C, то существует окрестность точки x0 такая, что во всех точках этой окрестности, кроме, быть может, самой токи x0, выполняется неравенство
и A > C, то существует окрестность точки x0 такая, что во всех точках этой окрестности, кроме, быть может, самой токи x0, выполняется неравенство  .
.
Доказательство. Возьмем ε = A – C.  , что при
, что при  выполняется
выполняется  , т.е.
, т.е.  . Но
. Но  и
и 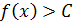 в этой окрестности. Теорема доказана.
в этой окрестности. Теорема доказана.
Теорема 3. Если  и для всех
и для всех  из некоторой окрестности точки
из некоторой окрестности точки  выполняется неравенство
выполняется неравенство  , то
, то  .
.
Доказательство. От противного. Пусть A > C. Тогда по теореме 2 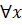 из некоторой окрестности будет
из некоторой окрестности будет  . Противоречие с условием теоремы. Теорема доказана.
. Противоречие с условием теоремы. Теорема доказана.
Теорема 4. Если функция имеет предел в точке  , то она ограничена в достаточно малой окрестности этой точки.
, то она ограничена в достаточно малой окрестности этой точки.
Доказательство. Пусть  . Возьмем
. Возьмем  .
.  , что
, что  при всех x,
при всех x,  . Так как
. Так как 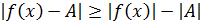 , то
, то  , т.е.
, т.е. 
 ,
, 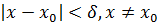 . Теорема доказана.
. Теорема доказана.
Бесконечно малые функции
Определение1. Функция  называется бесконечно малой функцией (или просто бесконечно малой) при
называется бесконечно малой функцией (или просто бесконечно малой) при  , если
, если 
Полагая в определении предела функции в точки по Коши A = 0, определение 1 запишем: 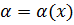 называется бесконечно малой, если
называется бесконечно малой, если  такое, что
такое, что  ,
, 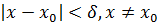 выполняется неравенство
выполняется неравенство  .
.
Теорема 1.  тогда и только тогда, когда
тогда и только тогда, когда  из достаточно малой окрестности токи
из достаточно малой окрестности токи  , где
, где  – бесконечна малая при
– бесконечна малая при  .
.
Доказательство. Необходимость. Пусть  , т.е.
, т.е.  , что
, что 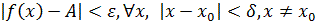 . Обозначим
. Обозначим 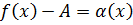 . Тогда
. Тогда 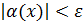 для тех же x, т.е.
для тех же x, т.е.  – бесконечна малая и
– бесконечна малая и  .
.
Достаточность.  ,
,  – бесконечна малая в токи
– бесконечна малая в токи  , т.е.
, т.е.  ,
,  . Значит
. Значит  при тех же x, т.е.
при тех же x, т.е. 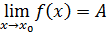 . Теорема доказана.
. Теорема доказана.
Лемма 1. Алгебраическая сумма двух бесконечно малых есть бесконечно малая.
Доказательство. Пусть  и
и  – две бесконечно малые в точке
– две бесконечно малые в точке  . Возьмем
. Возьмем  . Для
. Для 
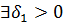 , что
, что
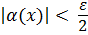
 . (1)
. (1)
и  , что
, что

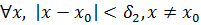 . (2)
. (2)
Пусть min{ 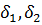 } =
} =  . Если
. Если  , то (1) и (2) выполняются одновременно. Имеем
, то (1) и (2) выполняются одновременно. Имеем  ,
,
т.е. 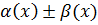 - бесконечно малые в точке
- бесконечно малые в точке  . Лемма доказана.
. Лемма доказана.
Лемма 2. Пусть функция 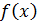 ограничена в некоторой окрестности точки
ограничена в некоторой окрестности точки  , а
, а  – бесконечна малая в токе
– бесконечна малая в токе  . Тогда
. Тогда  – бесконечно малая в точке
– бесконечно малая в точке  .
.
Доказательство. По условию теоремы  . Возьмем
. Возьмем  . Т.к.
. Т.к.  – бесконечно малая в точке
– бесконечно малая в точке  , то для
, то для  найдется
найдется  , что
, что 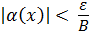
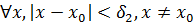 . Пусть min{
. Пусть min{ 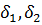 } =
} = 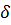 . Тогда если
. Тогда если 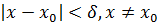 , то
, то  = ε. Лемма доказана.
= ε. Лемма доказана.
Следствие 1. Произведение бесконечно малой на постоянную есть бесконечно малая.
Следствие 2. Произведение бесконечно малых есть бесконечно малая.
Теоремы о пределах функций
Предел абсолютной величины.
Теорема 1. Если  , то
, то  .
.
Доказательство. Дано  , т.е.
, т.е.  , если
, если  ,
, 
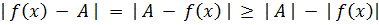 , т.е.
, т.е.  . Кратного
. Кратного  . Таким образом
. Таким образом  ,
,  ,
,  ,
,  . Теорема доказана.
. Теорема доказана.
Предел суммы.
Теорема 2. Если в точке  существуют пределы функции
существуют пределы функции  и
и  , то существуют и пределы функций
, то существуют и пределы функций  , причем
, причем  .
.
Доказательство. Пусть  ,
,  . По теореме 1 параграфа 15
. По теореме 1 параграфа 15  ,
,  ,
,  и
и  – бесконечно малые в точке
– бесконечно малые в точке  .
.  . По лемме 1 параграфа 15
. По лемме 1 параграфа 15  – бесконечно малые в точке
– бесконечно малые в точке  . Снова по теореме 1 параграфа 15
. Снова по теореме 1 параграфа 15  . Теорема доказана.
. Теорема доказана.
Легко обобщить на любое конечное число слагаемых.
Предел произведения.
Теорема 3. Если в точке  существуют пределы функции
существуют пределы функции  и
и  , то существуют и пределы функции
, то существуют и пределы функции  , причем
, причем  .
.
Доказательство. Пусть  ,
,  . Тогда
. Тогда  ,
,  ,
,  . Скобка – бесконечно малая в точке
. Скобка – бесконечно малая в точке  .
.  . Теорема доказана.
. Теорема доказана.
Следствие 1.  , c – const.
, c – const.
Действительно,  .
.
Следствие 2.  , k – натуральное число.
, k – натуральное число.
Действительно,  .
.
Предел частного.
Теорема 4. Если в точке  существуют пределы функции
существуют пределы функции  и
и  , причем
, причем  , то существует и предел функции
, то существует и предел функции  , причем
, причем 
 .
.
Доказательство. Пусть  ,
, 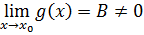 . Рассмотрим разность
. Рассмотрим разность  . Здесь
. Здесь  . Т.к.
. Т.к. 
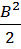 , то по теореме 2 параграфа 14 в достаточно малой окрестности точки
, то по теореме 2 параграфа 14 в достаточно малой окрестности точки  будет
будет 
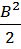 , т.е. 0 <
, т.е. 0 <  <
<  . Так что
. Так что  ограничена в соответствующей окрестности точки
ограничена в соответствующей окрестности точки  . Числитель является бесконечно малой при
. Числитель является бесконечно малой при  , т.к.
, т.к. 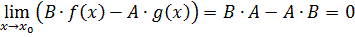 . В итоге
. В итоге  . Теорема доказана.
. Теорема доказана.
Пример. 


 .
.
|
из
5.00
|
Обсуждение в статье: Свойства функции, имеющей предел |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

