 |
Главная |
Непрерывность функции в точке
|
из
5.00
|
При рассмотрении  поведение функции
поведение функции 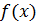 в точке
в точке  не учитывается. Если этот предел существует, то в точке
не учитывается. Если этот предел существует, то в точке  возможны случаи:
возможны случаи:
1)  в точке
в точке  не определена;
не определена;
2) 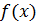 в точке
в точке  определена, но
определена, но 
3) в точке  определена и
определена и 
В особый класс функций выделяются те, у которых имеет место случай  .
.
Определение 1. Функция  , определенная на
, определенная на  , называется непрерывной в точке
, называется непрерывной в точке 
 , если предел функции в точке
, если предел функции в точке  равен значению функции в этой точке, т.е.
равен значению функции в этой точке, т.е. 
Используя определения предела, получим эквивалентые определения.
Определение 2. Функция  называется непрерывной в точке
называется непрерывной в точке 
 , если для любой последовательности {
, если для любой последовательности {  },
},  ,
, 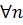 ,
,  , соответствующая последовательность значений функции {
, соответствующая последовательность значений функции {  } сходится к
} сходится к  .
.
Определение 3. Функция 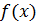 называется непрерывной в точке
называется непрерывной в точке 
 , если
, если 

 такое, что
такое, что  , |
, |  |<
|<  выполняется неравенство |
выполняется неравенство |  -
-  )|<
)|<  .
.
В определении предела функции в точке имеется еще условие
 (
(  ). В определениях 2 и 3 эти условия не нужны, т.к.
). В определениях 2 и 3 эти условия не нужны, т.к. 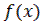 в точке
в точке  должна быть определена.
должна быть определена.
Разность  называется приращением аргумента в точке
называется приращением аргумента в точке  и обозначается через
и обозначается через  ;разность
;разность  называется приращением функции
называется приращением функции  в точке
в точке  и обозначается через
и обозначается через  ).Любое значение аргумента
).Любое значение аргумента  +
+  , причем
, причем  при
при  и
и  при
при  . Соответственно
. Соответственно  .
.
Определение 4. Функция 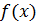 называется непрерывной в точке
называется непрерывной в точке  , если
, если 
 такое, что
такое, что  выполняется неравенство |
выполняется неравенство |  |<
|<  , если |
, если |  |<
|<  .
.
Это определение означает, что  в точке
в точке  является бесконечно малой функцией от
является бесконечно малой функцией от  , если
, если 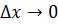 .
.
Определение 5. Функция  называется непрерывной в точке
называется непрерывной в точке  , если бесконечно малому приращению аргумента в точке
, если бесконечно малому приращению аргумента в точке  соответствует бесконечно малое приращение функции, т.е.
соответствует бесконечно малое приращение функции, т.е.  =0.
=0.
2
Свойство непрерывности является локальным свойством, т.е. зависит от поведения функции лишь вблизи точки  . Функция может быть непрерывна в одних и не быть таковой в других точках.
. Функция может быть непрерывна в одних и не быть таковой в других точках.
Пример 1.  .
. 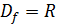 .
.  .
.
Пример 2. 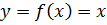 .
. 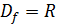 .
. 
Пример 3. 
 .
.  .
.  .
.
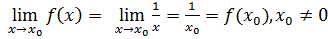 .
.
Пример 4.  .
. 
При |  |≤
|≤  имеем |
имеем |  |≤|
|≤| 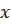 | (см. параграф 19). Если |
| (см. параграф 19). Если | 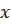 |>
|>  , то
, то
|  |< |
|< | 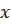 |, т.к. |
|, т.к. |  |<1. Так что |
|<1. Так что |  |≤|
|≤| 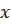 |,
|, 
|  |= |
|= |  -
-  |=|2
|=|2 
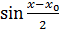 |≤2∙1∙
|≤2∙1∙ 
 , т.е
, т.е 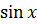 непрерывна в любой точке.
непрерывна в любой точке.
Если известно, что функция 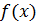 непрерывна в точке
непрерывна в точке  , то при вычислении предела
, то при вычислении предела  достаточно приравнять его
достаточно приравнять его 
Пример 5.  .
.
26. Непрерывность суммы,
произведения, частного
Теорема 1. Если функции  и
и 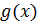 непрерывны в точке
непрерывны в точке  , то функции
, то функции  непрерывны в точке
непрерывны в точке 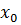 . Если, кроме того,
. Если, кроме того, 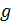 (
(  , то
, то 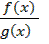 непрерывна в точке
непрерывна в точке  .
.
Доказательство. Доказательство следует из соответствующих свойств пределов функций (параграф 17). Т.к. доказательство во всех случаях одинаково, то рассмотрим один из случаев. Докажем для  . Пусть
. Пусть  =
=  ,
,  =
= 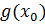 .
.
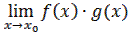 =
=  ∙
∙  =
=  ∙
∙ 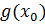 .
.
Теорема легко распространяется на любое конечное число функций.
Пример 1. 
 +…+
+…+  +
+  .
.  .
.
3
Функция  непрерывна в любой точке
непрерывна в любой точке 
 тоже непрерывна в любой точке
тоже непрерывна в любой точке 
 . Тогда
. Тогда  непрерывна в любой точке
непрерывна в любой точке  как сумма непрерывных функций.
как сумма непрерывных функций.
Пример 2.  =
=  .
. 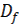 - все действительные числа, кроме нулей знаменателя. Числитель и знаменатель непрерывны
- все действительные числа, кроме нулей знаменателя. Числитель и знаменатель непрерывны 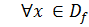 .
.
Следовательно,  непрерывна в любой точке, в которой знаменатель отличен от нуля.
непрерывна в любой точке, в которой знаменатель отличен от нуля.
27. Переход к пределу под знаком
непрерывной функции.
Непрерывность сложной функции
Теорема 1. Пусть задана сложная функция  (
(  и пусть
и пусть  , а функция
, а функция  непрерывна в точке
непрерывна в точке  . Тогда
. Тогда 
Доказательство. По условию
 ,
, 


Из  следует, что
следует, что 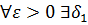 >0 такое, что
>0 такое, что
|  )|
)|  ,
,  , |
, |  |
| 

Из  по указанному
по указанному  >0 найдется
>0 найдется  >0 такое, что|
>0 такое, что|  |<
|< 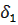 ,
, 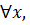
 x ≠
x ≠  .
.
Т.о.  , |
, |  выполняется неравенство |
выполняется неравенство |  , а следовательно и неравенство |
, а следовательно и неравенство |  -
-  |
|  . Это означает, что
. Это означает, что
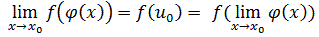 .Теорема доказана.
.Теорема доказана.
Теорема 2. Пусть функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  ) . Тогда сложная функция
) . Тогда сложная функция  (
(  ) ) непрерывна в точке
) ) непрерывна в точке  .
.
Доказательство. Из определения непрерывности функции в точке следует, что  определена в некоторой окружности точки
определена в некоторой окружности точки  .
.
Из непрерывности функции  и определения сложной функции
и определения сложной функции
4
следует, что сложная функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Значит, имеет смысл говорить о непрерывности этой функции в точке
. Значит, имеет смысл говорить о непрерывности этой функции в точке  .
.
У нас выполняются все условия теоремы 1, причем
 . Поэтому
. Поэтому  т.е.
т.е.  непрерывна в точке
непрерывна в точке  . Теорема доказана.
. Теорема доказана.
Пример 1.  . Непрерывна в любой точке (параграф 27,пример 4).
. Непрерывна в любой точке (параграф 27,пример 4).  . Непрерывна в любой точке
. Непрерывна в любой точке 
 .
.
 )
)  непрерывна по теореме 2 в любой точке
непрерывна по теореме 2 в любой точке  .
.
Пример
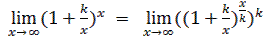 =(
=( 
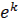 . Здесь
. Здесь  непрерывна при
непрерывна при 
28. Односторонняя непрерывность.
Точки разрыва
Определение 1. Если 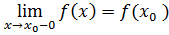 , то
, то  называется непрерывной слева, а если
называется непрерывной слева, а если  , то
, то  называется непрерывной справа в точке
называется непрерывной справа в точке  .
.
Функция  непрерывна в точке
непрерывна в точке  тогда и только тогда, когда
тогда и только тогда, когда  непрерывна в точке
непрерывна в точке  как слева, так и справа (теорема 1, параграф 20).
как слева, так и справа (теорема 1, параграф 20).
Пример 1.  .
. 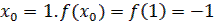


Функция непрерывна справа, не является непрерывной слева.
Определение 2. Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если не выполняется условие
, если не выполняется условие  .
.
Если  - точка разрыва функции f(x), то
- точка разрыва функции f(x), то
1. либо не существует  ;
;
2. либо  не определена в точке
не определена в точке  ;
;
3. либо  определена в точке
определена в точке  и имеет предел в этой точке, но
и имеет предел в этой точке, но  .
.
5
Определение 3. Точка разрыва  функции
функции  называется точкой разрыва 1 рода, если существуют конечные односторонние пределы
называется точкой разрыва 1 рода, если существуют конечные односторонние пределы
(оба) 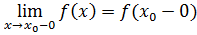 и
и  . Величина
. Величина
 (
(  называется скачком функции
называется скачком функции  в точке
в точке  . Если
. Если  то точка
то точка 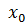 называется точкой устранимого разрыва, а разрыв устранимым.
называется точкой устранимого разрыва, а разрыв устранимым.
Определение 4. Точка разрыва  функции
функции  называется точкой разрыва 2 рода, если хотя бы один из односторонних пределов в точке
называется точкой разрыва 2 рода, если хотя бы один из односторонних пределов в точке  не существует.
не существует.
Здесь как и всегда под пределом понимаем конечное число. Разрыв 2 рода называется бесконечным, если хотя бы один из односторонних
пределов бесконечен.
Пример 1.  ,
,  . В точке
. В точке  разрыв 1 рода. Скачок
разрыв 1 рода. Скачок 
Пример 2 . 
| 
|

| ± 
| ± 
| ± | ±2 
|

|
|  1 1
| 0,9 | 0,64 | 0 | -0,21 | 0 | 0,13 |
 .
.
В точке  разрыв 1 рода, устранимый.
разрыв 1 рода, устранимый.
Доопределив  , устраняем разрыв. Новая функция непрерывна
, устраняем разрыв. Новая функция непрерывна  .
.
Пример 3. 
 . Но
. Но  Разрыв 1 рода , устранимый. Положив
Разрыв 1 рода , устранимый. Положив  , получим непрерывную функцию.
, получим непрерывную функцию.
Пример 4. 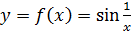 .
.
 не существуют. (параграф 11, пример 3). Разрыв 2 рода.
не существуют. (параграф 11, пример 3). Разрыв 2 рода.
Пример 5.  ;
;  ,
,  .Разрыв 2 рода, бесконечный.
.Разрыв 2 рода, бесконечный.
29. Пределы и точки разрыва монотонной функции
Теорема 1. Если функция  не убывает на
не убывает на  , то в точках
, то в точках 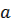 и
и  существуют конечные или бесконечные пределы
существуют конечные или бесконечные пределы 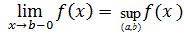 ,
,
 . Если
. Если  не возрастает на
не возрастает на  , то
, то
 ,
,  .
.
Доказательство. Пусть 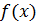 не убывает на
не убывает на  , и ограничена сверху. Тогда существует верхняя грань множества всех значений функции
, и ограничена сверху. Тогда существует верхняя грань множества всех значений функции 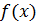 для
для 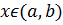
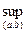
 По определению верхней грани
По определению верхней грани
 что
что  Возьмем
Возьмем  Т.к.
Т.к.  ≥
≥ 
 , то при
, то при  -
- 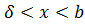 будет
будет  Т.к.
Т.к.  произвольно, то это означает, что
произвольно, то это означает, что 
Если  не убывает и неограниченна сверху на
не убывает и неограниченна сверху на  , то
, то

 что
что  Возьмем
Возьмем 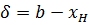 .
.  (
(  ) имеем
) имеем  , т.е.
, т.е. 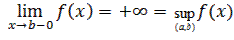 .
.
Для неубывающей функции доказательство аналогично.
Следствие. Если функция  монотонна на
монотонна на 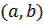 , то в каждой точке интервала она имеет конечные пределы как слева, так и справа.
, то в каждой точке интервала она имеет конечные пределы как слева, так и справа.
Доказательство. Пусть  не убывает на
не убывает на  .
. 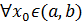 будет
будет
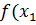 )≤
)≤  )≤
)≤ 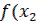 ), где
), где 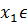 (
(  ),
),  . Поэтому
. Поэтому

 )
)  .
.
Пределы  и
и  существует по теореме 1 и конечны по предыдущему неравенству.
существует по теореме 1 и конечны по предыдущему неравенству.
Теорема 2.Если функция  монотонна на
монотонна на  , то она может иметь разрывы только 1 рода.
, то она может иметь разрывы только 1 рода.
Доказательство. Все значения функции заключены между  и
и  , т.е.
, т.е.  ограничена на
ограничена на  . В
. В  функция
функция 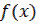 имеет конечные односторонние пределы
имеет конечные односторонние пределы  и
и  +0) в силу следствия теоремы 1. Тогда если
+0) в силу следствия теоремы 1. Тогда если  -точка разрыва, то это разрыв 1 рода. Теорема доказана.
-точка разрыва, то это разрыв 1 рода. Теорема доказана.
30. Промежуточные значения непрерывной функции
Определение 1. Функция 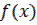 называется непрерывной на
называется непрерывной на  ,если она непрерывна в каждой точке этого интервала. Функция
,если она непрерывна в каждой точке этого интервала. Функция 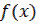 непрерывна на
непрерывна на  , если она непрерывна в каждой внутренней точке сегмента, непрерывна справа в точке а и непрерывна слева в точке
, если она непрерывна в каждой внутренней точке сегмента, непрерывна справа в точке а и непрерывна слева в точке  .
.
Непрерывность на промежутках других видов определяется аналогично. Теорема 1 . ( теорема Больцано ).Если  непрерывна на
непрерывна на  и на концах сегмента принимает значения разных знаков, то существует по крайней мере одна внутренняя точка
и на концах сегмента принимает значения разных знаков, то существует по крайней мере одна внутренняя точка  этого сегмента
этого сегмента  в которой
в которой  .
.
Доказательство. Пусть для определенности  ,
,  . Разделим
. Разделим  пополам точкой
пополам точкой  . Если
. Если  )=0, то теорема доказана. Если
)=0, то теорема доказана. Если  , то на концах одной из половин функции
, то на концах одной из половин функции  принимает значения разных знаков. Обозначим эту половину через [
принимает значения разных знаков. Обозначим эту половину через [ 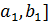 ,
,  ) < 0,
) < 0,  ) > 0. Снова разделим [
) > 0. Снова разделим [  ] пополам. Если
] пополам. Если  )
)  0, то теорема доказана. Если нет, то имеем [
0, то теорема доказана. Если нет, то имеем [ 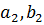 ],
], 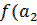 )<0,
)<0, 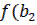 )>0 и т.д.
)>0 и т.д.
Могут быть две возможности.
1)  )=0 при некотором
)=0 при некотором  . Теорема доказана.
. Теорема доказана.
2) Процесс продолжается неограниченно. Имеем систему вложенных сегментов 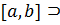 [
[  ] ⊃…⊃[
] ⊃…⊃[  ] ⊃
] ⊃ 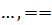 0. По принципу вложенных отрезков ( параграф 23,теорема 3) существует единственная точка
0. По принципу вложенных отрезков ( параграф 23,теорема 3) существует единственная точка  такая, что
такая, что  ,
,  ,
,  . По условию теоремы функция
. По условию теоремы функция 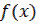 непрерывна на т.е. непрерывна
непрерывна на т.е. непрерывна  и в точке
и в точке  . Значит
. Значит  ,
,  .Т.к.
.Т.к.  ,
, 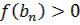 , то, переходя здесь к пределу получаем
, то, переходя здесь к пределу получаем  ,
,
 , Т.к.
, Т.к.  ,то
,то 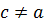 ;
;  , то
, то  ;
;
8
так что  . Теорема доказана.
. Теорема доказана.
Теорема 2. Если  непрерывна на
непрерывна на  и на концах сегмента принимает не равные значения, то функция
и на концах сегмента принимает не равные значения, то функция  на
на 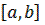 принимает любое значение, промежуточное между
принимает любое значение, промежуточное между  и
и  .
.
Доказательство. Пусть  - произвольное число, удовлетворяющее условию
- произвольное число, удовлетворяющее условию  Рассмотрим функцию
Рассмотрим функцию
 . Она непрерывна на
. Она непрерывна на  причем
причем  и
и  . По теореме 1 т.е.
. По теореме 1 т.е.  .Теорема доказана.
.Теорема доказана.
33. Непрерывность обратной функции
Определение 1. Функция  называется инъективной, если для любых двух различных точек
называется инъективной, если для любых двух различных точек  ,
,  функции
функции 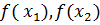
тоже различны.
Пусть  инъективна. Возьмем любую точку
инъективна. Возьмем любую точку  . Для нее найдется
. Для нее найдется  что
что  , причем другой точки
, причем другой точки  ,
,  , нет. Если таким образом каждой точке
, нет. Если таким образом каждой точке  мы поставим в соответствие ту единственную точку
мы поставим в соответствие ту единственную точку  , для которой
, для которой  ,то на множестве Е будет определена некоторая функция переменной
,то на множестве Е будет определена некоторая функция переменной  . Эта функция называется обратной по отношению к функции
. Эта функция называется обратной по отношению к функции  и обозначается через
и обозначается через  . Так что обратную функцию можно определить только для инъективной функции. Из определения 1 следует, что
. Так что обратную функцию можно определить только для инъективной функции. Из определения 1 следует, что  тоже инъективна и имеют место равенство:
тоже инъективна и имеют место равенство:
(  ,
, 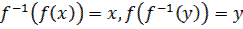
Пример 1. 1)  .
.  . Инъективна
. Инъективна  .
.
2)  .
. 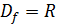 . На
. На 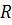 она не инъективна, т.к.
она не инъективна, т.к.  На множестве
На множестве  функция инъективна и здесь
функция инъективна и здесь 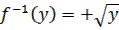
Теорема 1. Всякая строго монотонная функция  имеет обратную функцию.
имеет обратную функцию.
Доказательство. Пусть  монотонно возрастает, т.е. при
монотонно возрастает, т.е. при  <
<  имеем
имеем  <
<  . Это значит, что
. Это значит, что 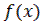 инъективна и потому имеет обратную функцию. Теорема доказана.
инъективна и потому имеет обратную функцию. Теорема доказана.
Если функция  строго кусочно-монотонна в
строго кусочно-монотонна в  , то
, то  можно разбить на промежутки так, что в ка
можно разбить на промежутки так, что в ка
|
из
5.00
|
Обсуждение в статье: Непрерывность функции в точке |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

