Сведения из линейной алгебры

Глава 10. Метод межотраслевого баланса и балансовые модели анализа и прогнозирования отраслевых показателей

Теоретические основы межотраслевого баланса были разработаны в СССР в 1923—1924 гг. В 1930-е годы Василий Леонтьев применил метод анализа межотраслевых связей с привлечением аппарата линейной алгебры для исследования экономики США. Метод стал известен под названием «затраты — выпуск» (input-output). В 1970—1980-х годах в СССР на основе данных межотраслевых балансов разрабатывались сложные межотраслевые модели и модельные комплексы, которые использовались в прогнозных расчетах и частично входили в технологию народнохозяйственного планирования. В этой области работали известные ученые-экономисты: В. С. Немчинов,   А. Н. Ефимов, Э. Ф. Баранов, Л. Я. Берри, Э. Б. Ершов, Ф. Н. Клоцвог, В. В. Коссов, Л. Е. Минц, С. С. Шаталин, М. Р. Эйдельман.

В настоящее время Госкомстат Беларуси  проводит составление МОБ в концепции системы национальных счетов (МОБ СНС), на основе которого в РБ разработаны межотраслевые модели прогнозирования основных показателей социально-экономического развития Республики.

В комплексе модельных инструментов межотраслевого баланса (МОБ) ведущую роль играют статическая и динамическая модели МОБ. В теме приведены методологические и методические аспекты построения и использования моделей межотраслевого баланса на макроуровне и на уровне предприятий, а также основные сведения из линейной алгебры, которая выступает как математическая база моделей МОБ. Более подробную информацию можно найти в учебниках [1–16].

 

Сведения из линейной алгебры

Основные определения.  Матрицей называют прямоугольную таблицу чисел. Чтобы подчеркнуть размеры матрицы A, пишут: A_m´n, и читают: матрица размеров m на n. Это значит, что матрица состоит из m строк и n столбцов.  Числа, из которых составлена матрица, называются элементами матрицы.

При двухиндексном обозначении элементов a_ij матрицы A первый индекс всегда обозначает номер строки, а второй индекс – номер столбца, на пересечении которых стоит данный элемент.

Записывают матрицы как таблицы заключенные в круглые или квадратные скобки, а иногда коротко . Последнее выражение означает, что матрица A размеров m´n,элементами которой являются числа a_ij, i=1,…m, j=1,…n .

Матрицы, состоящие из одной строки или одного столбца, часто называют векторами.

Две матрицы называются равными, если они одинаковых размеров и соответствующие элементы их равны.

Матрица, у которой все элементы нули, называется нулевой матрицей. Ее обычно обозначают буквой O.

Матрица, у которой число строк равно числу столбцов, называется квадратной. Порядком квадратной матрицы называется число ее строк (или столбцов).

Элементы a₁₁, a₂₂, …, a_nn составляют главную диагональ квадратной матрицы A порядка n .

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю.

Диагональная матрица называется единичной, если на главной диагонали стоят единицы. Обозначают единичную матрицу буквами E или I.

Операции над матрицами. Суммой A+B двух матриц и  одинаковых размеров называется матрица  такая, что c_ij= a_ij +b_ij,  

Произведением aA (или Aa) матрицы на число a называется матрица такая, что b_ij=aa_ij,   .

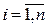Произведением двух матриц и  на матрицу называется матрица  такая, что    

Отметим, что две матрицы можно перемножать лишь в том случае, когда число столбцов первой равно числу строк второй. Если матрицу A можно умножить на B, то из этого не следует, что можно умножить матрицу B на A. Если даже существуют произведения AB и BA, то может быть AB¹BA.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной данной.

Матрицу, транспонированную к матрице A, обозначают A^T или A'.

Блочные матрицы. Частоприходится использовать матрицы разбитые на прямоугольные части, которые называют блоками. Если матрица A разбита на блоки, то ее можно представить в виде

,

где элементами матрицы A являются матрицы A_ij. Заметим, что матрицы A_ij при фиксированном i имеют одинаковое число строк, а при фиксированном j имеют одинаковое число столбцов.

Если две матрицы имеют одинаковые размеры и разбиты на одинаковые блоки, то их можно складывать по тому же правилу, как и обыкновенные матрицы.

Умножение блочной матрицы A=(A_ij) на блочную матрицу B=(B_ij) возможно лишь в том случае, когда число блоков в строке матрицы A равен число блоков столбце матрицы B. Для возможности блочного умножения дополнительно требуется, чтобы при разбиении на блоки все горизонтальные размеры в первом сомножителе совпадали с соответствующими размерами во втором

Тогда матрица С=AB будет иметь блочный вид

,

где       

Определитель матрицы.  Определителем квадратной матрицы будем называть число, поставленное по ниже приведенному правилу в соответствие данной матрице. Определитель матрицы A обозначают detA или |A|.

Для обозначения определителя матрицы употребляется также следующий символ: выписывается матрица, но заключаются ее элементы вместо круглых или квадратных скобок в прямоугольные черточки.

1. Определителем матрицы первого порядка A=(a₁₁) называют число detA= a₁₁.

2. Определителем матрицы второго порядка  называют число .

Чтобы ввести понятие определителя для матриц порядка выше второго проведем необходимые вспомогательные построения.

Дополнительным минором  элемента a_ij квадратной матрицы A называют определитель матрицы, полученной из A вычеркиванием из нее i-ой строки и j-ого столбца.

Алгебраическим дополнением до элемента a_ij матрицы A называется величина

3. Определителем матрицы A n-го порядка называют число .

Теорема. Определитель n-го порядка может быть вычислен по одной из формул

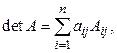
Обратная матрица. Матрица B называется обратной для квадратной матрицы A, если AB=BA=E. Матрицу обратную для матрицы A обозначают .

Квадратная матрица A называется невырожденной, если ее определитель отличен от нуля. Если определитель матрицы равен нулю, то матрица называется вырожденной.

Теорема. Для невырожденной матрицы A существует единственная обратная матрица , которая может быть вычислена следующим образом:

где  – алгебраическое дополнение до элемента a_ij матрицы A.

Решение системы n линейных уравнений с n неизвестными. Пусть дана система

                          (10.1)

Здесь  и  - заданные числа. Числа  называются коэффициентами системы,  - свободными членами, а символы  - неизвестными. Решением системы называется такая упорядоченная система чисел , которая при подстановке в систему (10.1)  на место неизвестных 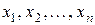 обращает все уравнения в тождества.

Матрица

составленная из коэффициентов системы, называется матрицей системы.

Обозначим

Тогда система (10.1) может быть записана в матричной форме

AX=B.                                  (10.2)

Если матрица A невырожденная, то, умножая систему (10.2) слева на , получим ее решение

                                 (10.3)

Из формулы (10.3) легко получаются формулы Крамера [6], согласно которым решение находится по формулам

где  а определители  получаются из определителя  заменой i-го столбца столбцом B.

 Ранг матрицы.  Выделим в матрице  k строк с номерами  и k столбцов с номерами . Элементы, расположенные на пересечении выделенных строк и столбцов, образуют квадратную матрицу k -го порядка, определитель которой называется минорном k -го порядка матрицы A и обозначается .

 Рангомматрицы называется наивысший порядок отличных от нуля ее миноров.

Можно дать другое определение ранга матрицы. Для этого введем важные понятия.

Строки (столбцы)  матрицы A называются линейно-зависимыми, если существует ненулевой набор чисел  (не все  равны нулю) таких, что имеет место равенство

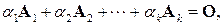                             (10.4)

где O – нулевая строка (столбец).

Строки (столбцы)  матрицы A называются линейно-независимыми, если равенство (3.1.4) имеет место лишь в том случае, когда все  равны нулю.

Рангом матрицы называют максимальное число линейно-зависимых строк (столбцов) матрицы.

Элементарными пре образованиями матрицы называется:

1) умножение строки или столбца матрицы на число отличное от нуля;

2) пребавление к какой-либо стороке или столбцу другой стороки или столбца умножения на число;

3) перестановки строк или столбцов.

Теорема. Элементарные преобразования матрицы не меняют ранга матрицы.

Элементарные преобразования матрицы A могут быть использованы для вычисления обратной матрицы. Строится матрица B=(A E), которая состоит из двух блоков: матрицы A и расположенной за ней единичной E тех же размеров , что и матрица A. Если умножить матрицу  на матрицу B, то получим  Следовательно, выполняя элементарные преобразования над строками матрицы B таким образом, чтобы на месте матрицы A получилась единичная матрица – на месте единичной матрицы получим .

С истемы m линейных уравнений с n неизвестными. Рассмотрим систему (10.2) с прямоугольной матрицей A_m´n, где m и n произвольные натуральные числа. Система (10.2) называется совместной, если она имеет по крайней мере одно решение. Система, не имеющая решений, называется несовместной.

Матрица составленная из коэффициентов системы называется матрицей системы, а матрица

,

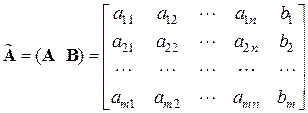у которой в матрице системы добавлен столбец правых частей, называется расширенной матрицей системы.

Теорема Кронекера-Капелли. Для совместности линейной системы необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы этой системы.

Ранг r матрицы совместной системы не может быть больше числа неизвестных n. Поэтому могут быть два случая:

1) если r = n, то система имеет единственное решение;

2) если r<n, то система имеет бесконечное множество решений.

Для построения решения системы линейной уравнений является понятие базисного минора.

Базисным минором матрицыназывается отличный от нуля минор, порядок которого равен рангу матрицы.

Неизвестные системы линейных уравнений, коэффициенты при которых образуют базисный минор, называются базисными, а остальные – свободными.

Для решения системы необходимо определить ранг матрицы, найти базисный минор и выделить базисные и свободные неизвестные. Затем отбросить уравнения, коэффициенты которых не входят в базисный минор. В оставшихся уравнениях слагаемые, содержащие свободные переменные, перенести в правую часть и присвоить им произвольные числовые значения. Решить полученную систему относительно базисных неизвестных можно, например, используя правило Крамера.

Из наиболее распространенных методов решения линейных систем следует выделить методы Гаусса и Гаусса – Жордана, подробно описанные в [1,2,5].