 |
Главная |
Статистическая модель МОБ «затраты-выпуск»
|
из
5.00
|
Матрица коэффициентов прямых затрат. Модели отчетного МОБ в виде соотношений (10.5) и (10.6) непригодны для прогнозных практических расчетов в силу открытого характера модели: 3 эндогенные переменные и 12 экзогенных, при этом экзогенные переменные также находятся между собой в определенной взаимосвязи. Поэтому определение элементов промежуточного потребления осуществляют на базе нормативов, называемых на макроуровне коэффициентами прямых затрат или технологическими коэффициентами. По данным отчетного МОБ (табл. 10.1) коэффициенты могут быть рассчитаны путем деления величин межотраслевых потоков на валовую продукцию потребляющих отраслей. Так, если первой отраслью является производство электроэнергии, а второй – легкая промышленность, то коэффициент a12 прямых затрат электроэнергии на единицу продукции легкой промышленности будет равен
 .
.
Аналогично можно рассчитать коэффициент a11 прямых затрат электроэнергии на единицу производства электроэнергии
 .
.
Для любой пары отраслей в общем случае коэффициент прямых затрат  составляет:
составляет:


 (10.7)
(10.7)
и характеризует количество продукции i -й отрасли, которое необходимо для производства единицы валовой продукции j-й отрасли. При i = j имеем коэффициент затрат собственной продукции отрасли на единицу валового выпуска.
Коэффициенты прямых затрат образуют квадратную матрицу A, содержащую в общем случае n -строк и n - столбцов:

Матрицу A называют матрицей коэффициентов прямых затрат или технологической матрицей. Ее особенность состоит в том, что при отсутствии в экономике технологических изменений технологическая матрица A постоянная.
Пример 10.3. На базе четырехотраслевого отчетного МОБ примера 10.1 рассчитать матрицу коэффициентов прямых затрат и дать их экономическую интерпретацию.
Решение. Матрицу коэффициентов прямых затрат А удобно рассчитывать по данным таблицы 10.4, где в одной таблице представлены межотраслевые потоки промежуточного продукта и валовые выпуски отраслей.
Матрица коэффициентов прямых затрат ( aij ) n * n рассчитывается на основе отчетного МОБ по формуле (10.7).
Для нашей задачи в соответствии с этой формулой, получаем:
 =
=  = 0,52,
= 0,52,
 =
=  = 0,12,
= 0,12,
и т.д.
Вычисления оформляются в виде матрицы прямых затрат  =
=
 ( млрд. д.е./ млрд. д.е.)
( млрд. д.е./ млрд. д.е.)
Показатели первого столбца показывают, что для производства валовой продукции промышленности на сумму 1 млрд. д.е. необходимо израсходовать валовой продукции промышленности на сумму 0,52 млрд. д.е. (520 млн. д.е.); продукции строительства на сумму 0,07 млрд. д.е.. (70 млн. д.е.); продукции прочих отраслей материального производства на сумму 40 млн. д.е.; объем услуг в размере 50 млн д.е.
Аналогичную интерпретацию имеют элементы остальных столбцов матрицы.
В частности элементы второго столбца показывают, что для производства валовой продукции строительства на сумму 1 млрд. д.е. необходимо израсходовать валовой продукции промышленности на сумму 0,12 млрд. д.е. (120 млн. д.е.)); продукции строительства на сумму 0,35 млрд. д.е. (350 млн. д.е.); продукции прочих отраслей материального производства на сумму 30 млн. д.е..; объем услуг в размере 30 млн. д.е..
Из формулы (10.7) следует, что



В этих обозначениях модель (10.5) может быть переписана в виде:


 (10.8)
(10.8)

Или в общем случае:



………………………… ( 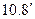 )
)

Модель ( 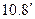 ) является базовой прогнозной моделью МОБ связи отраслевых структур валового выпуска и конечного спроса.
) является базовой прогнозной моделью МОБ связи отраслевых структур валового выпуска и конечного спроса.
Перепишем модель (  ) в матричной форме, введя предварительно следующие обозначения:
) в матричной форме, введя предварительно следующие обозначения:
 - вектор валовой продукции отраслей,
- вектор валовой продукции отраслей,
 - вектор конечного спроса на продукцию отраслей,
- вектор конечного спроса на продукцию отраслей,
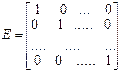 - единичная матрица.
- единичная матрица.
Тогда в матричном виде модель (  ) запишется:
) запишется:
 (10.9)
(10.9)
Система уравнений (10.9) содержит n уравнений и 2 n неизвестных. Такая система является неопределенной и имеет бесконечное множество решений. Для однозначного решения системы необходимо произвольно задать любые n неизвестные величины, тогда значения остальных n неизвестных будут определяться однозначно решением системы (10.9).
Модель (10.9) можно преобразовать следующим образом
 (10.10)
(10.10)
При условии, что матрица  обратима , последнее выражение можно записать в виде:
обратима , последнее выражение можно записать в виде:
 (10.11)
(10.11)
В экономической литературе матрицу  называют матрицей полных затрат и обозначают В:
называют матрицей полных затрат и обозначают В:
 . (10.12)
. (10.12)
Исследование обратимости матрицы  тесно связано с исследованием матрицы прямых затрат А на продуктивность, в рамках которого проверяется выполнение условия
тесно связано с исследованием матрицы прямых затрат А на продуктивность, в рамках которого проверяется выполнение условия  , что с позиций экономической интерпретации эквивалентно требованию (в соответствии с (10.10))
, что с позиций экономической интерпретации эквивалентно требованию (в соответствии с (10.10))  , т.е. поставки продукции отраслей в сферу конечного использования должны быть положительными элементами.
, т.е. поставки продукции отраслей в сферу конечного использования должны быть положительными элементами.
Рассмотрим более подробно понятие продуктивности технологической матрицы А.
Будем называть неотрицательную матрицу А продуктивной, если существует такой неотрицательный вектор 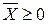 , что
, что 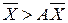 . В литературе [7,8,9] известен ряд критериев проверки продуктивности матрицы.
. В литературе [7,8,9] известен ряд критериев проверки продуктивности матрицы.
Для того, чтобы матрица коэффициентов прямых затрат была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
1). Матрица  неотрицательна обратима, т.е. существует обратная матрица
неотрицательна обратима, т.е. существует обратная матрица 
2). Матричный ряд  сходится, причем его сумма равна обратной матрице
сходится, причем его сумма равна обратной матрице 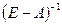 .
.
Но практическая проверка этих критериев является достаточно трудоемкой . Более простым, но только достаточным признаком продуктивности матрицы А является ограничение на величину наибольшей из сумм элементов матрицы А в каждом столбце  .
.
Приведенные математические условия продуктивности матрицы являются трудно экономически интерпретируемыми. Поэтому полезным представляется следующее утверждение.
Утверждение 10.1. Если в экономике не существует отраслей с нулевой и отрицательной валовой добавленной стоимостью, то матрица А, описывающая технологические процессы в такой экономике, является продуктивной.
Доказательство. В соответствии с системой уравнения (  ) и выражением (10.7) соотношение между промежуточными затратами и валовым выпуском j-й отрасли может быть записано в виде:
) и выражением (10.7) соотношение между промежуточными затратами и валовым выпуском j-й отрасли может быть записано в виде:
 ,
,  .
.
Поскольку валовая добавленная стоимость, исходя из положений утверждения– положительное число, т.е. zj >0  , то
, то


Или, при  ,
,
 ,
,  ,
,
что является достаточным условием продуктивности матрицы А.
При условии, что матрица А продуктивна, на основе модели (10.9) можно проводить следующие варианты расчета:
1. В модели задана валовая продукция отраслей (  ). Продукция отраслей, которая поступит в сферу конечного использования (
). Продукция отраслей, которая поступит в сферу конечного использования (  ), определяется в результате модельного расчета.
), определяется в результате модельного расчета.
2. В модели задан конечный спрос на продукцию отраслей (  ). На основе модельных расчетов можно определить требуемый для обеспечения данного конечного спроса валовой выпуск отраслей (
). На основе модельных расчетов можно определить требуемый для обеспечения данного конечного спроса валовой выпуск отраслей (  ).
).
3. По отдельным отраслям в модели задаются объемы валовой продукции ( 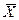 ), по другим — конечного выпуска (
), по другим — конечного выпуска (  ), но при этом число экзогенно задаваемых переменных должно совпадать с количеством рассматриваемых отраслей. Решение системы дает значения остальных переменных. Из экономического смысла целесообразно известными полагать: валовую продукцию ресурсообразующих отраслей (электроэнергетика, топливная и др.), а также конечный спрос на продукцию отраслей потребительского комплекса (легкая, пищевая и другие).
), но при этом число экзогенно задаваемых переменных должно совпадать с количеством рассматриваемых отраслей. Решение системы дает значения остальных переменных. Из экономического смысла целесообразно известными полагать: валовую продукцию ресурсообразующих отраслей (электроэнергетика, топливная и др.), а также конечный спрос на продукцию отраслей потребительского комплекса (легкая, пищевая и другие).
Замечание 10.1. В модели (10.9) предполагается, что на прогнозный период известна матрица прямых затрат А . Исходя из экономического содержания представленной модели, следует отметить, что коэффициенты прямых затрат  характеризуют в обобщенном виде технологию производства на макроуровне. Если принять во внимание определенную инерционность технологических процессов, можно принять предпосылку о неизменности нормативов расхода материалов и, следовательно, постоянстве технологической матрицы. В том случае, если данное предположение неверно, необходимо осуществить автономный прогноз коэффициентов матрицы прямых затрат на прогнозный период. В любом случае полагаем, что в модели (10.9) матрица А задается экзогенно.
характеризуют в обобщенном виде технологию производства на макроуровне. Если принять во внимание определенную инерционность технологических процессов, можно принять предпосылку о неизменности нормативов расхода материалов и, следовательно, постоянстве технологической матрицы. В том случае, если данное предположение неверно, необходимо осуществить автономный прогноз коэффициентов матрицы прямых затрат на прогнозный период. В любом случае полагаем, что в модели (10.9) матрица А задается экзогенно.
Решение систем линейных уравнений с использованием ППП. Сведения из линейной алгебре по математическим методам решения систем линейных уравнений изложены в п.10.1. Сейчас мы рассмотрим реализацию последних в системе Excel и с использованием специальных ППП.
Продемонстрируем их, используя данные примера 10.3.
Способ 1. Реализация матричного метода решения модели МОБ (10.9) соответственно формуле (10.11) предполагает
а) нахождение обратной матрицы к матрице (Е-А) (расчет матрицы полных затрат В);
б) выполнение операции умножения матриц полных затрат В и вектор-столбца конечного использования Y . Для определенности будем предполагать, что матрица (А) представлена матрицей примера 10.3 и имеет размерность 4´4.
Сначала опишем процедуру нахождения обратной матрицы к матрице (Е-А) (расчет матрицы полных затрат В) в Excel и ППП.
Сформируем искомую матрицу (Е-А)
 =
=  ,
,
и найдем обратную ей матрицу:
 ,
,
где в числителе матрица, присоединенная к матрице (Е-А), элементы которой представляют собой алгебраические дополнения для элементов транспонированной матрицы  , а в знаменателе – определитель матрицы (Е-А). Алгебраические дополнения в свою очередь для элемента с индексами i и j получаются умножением множителя
, а в знаменателе – определитель матрицы (Е-А). Алгебраические дополнения в свою очередь для элемента с индексами i и j получаются умножением множителя 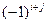 на минор, получаемый после вычеркивания из матрицы i -й строки и j -го столбца.
на минор, получаемый после вычеркивания из матрицы i -й строки и j -го столбца.
После нахождения обратной матрицы, выполнимоперацию умножения матриц полных затрат В и вектор-столбца конечного использования  , что реализует модель МОБ в матричной форме имеет вид аналогичный (10.11):
, что реализует модель МОБ в матричной форме имеет вид аналогичный (10.11):
 ,
,
где матрица полных затрат В найдена на предыдущем этапе, а вектор–столбец конечного использования продукции отраслей имеет вид:  .
.
Реализация в Excel . Нахождение обратной матрицы. Введем элементы матрицы (Е-А) в диапазон ячеек А4:D7. Выделим область (диапазон из 16-ти ячеек) E4:H7 для размещения обратной матрицы. Найдем обратную матрицу с помощью функции МОБР, для чего: выполним один щелчок левой кнопки мыши по кнопке  (вставка функции) стандартной панели инструментов (на экране диалоговое окно Мастер функций).
(вставка функции) стандартной панели инструментов (на экране диалоговое окно Мастер функций).
В левом окне подведем курсор на категорию Математические и выделим ее щелчком кнопки мыши. В поле Функция этого окна с помощью кнопок прокрутки найдем функцию МОБР ивыделим ее щелчком по мыши и нажмем кнопку ОК (рис. 10.1).
Рис. 10.1. Диалоговое окно активизации команды обращения матрицы.
В поле Массив с мигающим курсором введем диапазон размещения элементов матрицы (Е-А) – A4: D7 и нажмем клавиши <Ctrl>+<Shift>+<Enter> (одновременным нажатием этих клавиш мы указываем программе, что она должна выполнить операцию над массивами) (рис.10.2.).

Рис. 10.2. Диалоговое окно ввода данных инструмента МОБР.
На экране в выделенном диапазоне получим обратную матрицу. В нашем примере искомая обратная матрица приведена на рис. 10.3.
|
| Матрица (Е-А) |
| Обратная матрица |
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,48 | -0,12 | -0,04 | -0,2 | 2,233073 | 0,451158 | 0,184553 | 0,658239 |
| -0,07 | 0,65 | -0,03 | -0,12 | 0,277656 | 1,60969 | 0,103653 | 0,329007 |
| -0,04 | -0,03 | 0,7 | -0,14 | 0,171212 | 0,113615 | 1,461256 | 0,315565 |
| -0,05 | -0,03 | -0,04 | 0,8 | 0,15854 | 0,094242 | 0,088484 | 1,319256 |
Рис. 10.3. Результат применения инструмента.
Умножение матриц. Занесем вектор  в ячейки А9:А12. Выделим диапазон Е9:Е12 для размещения вектора решений
в ячейки А9:А12. Выделим диапазон Е9:Е12 для размещения вектора решений  . Умножение матриц В и
. Умножение матриц В и  выполним с помощью функции МУМНОЖ, для чего: выполним один щелчок левой кнопки мыши по кнопке
выполним с помощью функции МУМНОЖ, для чего: выполним один щелчок левой кнопки мыши по кнопке  (вставка функции) стандартной панели инструментов (на экране диалоговое окно Мастер функций). В левом окне подведем курсор на категорию Математические и выделим ее щелчком кнопки мыши. В поле Функция этого окна с помощью кнопок прокрутки найдем функцию МУМНОЖ ивыделим ее щелчком по мыши и нажмем кнопку ОК (рис. 10.4).
(вставка функции) стандартной панели инструментов (на экране диалоговое окно Мастер функций). В левом окне подведем курсор на категорию Математические и выделим ее щелчком кнопки мыши. В поле Функция этого окна с помощью кнопок прокрутки найдем функцию МУМНОЖ ивыделим ее щелчком по мыши и нажмем кнопку ОК (рис. 10.4).
Рис. 10.4. Диалоговое окно активизации команды умножения матриц
В поле Массив1 с мигающим курсором введем диапазон размещения элементов матрицы В – Е4: Н7, в поле Массив2 с мигающим курсором введем диапазон размещения элементов матрицы  - А9:А12 и нажмем клавиши <Ctrl>+<Shift>+<Enter> (рис.10.5.).
- А9:А12 и нажмем клавиши <Ctrl>+<Shift>+<Enter> (рис.10.5.).

Рис. 10.5. Диалоговое окно ввода данных инструмента МУМНОЖ.
На экране в выделенном диапазоне, в ячейках Е9:Е12, получим вектор-столбец произведения матриц. Это означает, что значения неизвестных:  ,
, 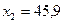 ,
,  ,
,  .
.
|
| Матрица (Е-А) |
|
| Матрица полных затрат | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,48 | -0,12 | -0,04 | -0,2 | 2,233073 | 0,451158 | 0,184553 | 0,658239 |
| -0,07 | 0,65 | -0,03 | -0,12 | 0,277656 | 1,60969 | 0,103653 | 0,329007 |
| -0,04 | -0,03 | 0,7 | -0,14 | 0,171212 | 0,113615 | 1,461256 | 0,315565 |
| -0,05 | -0,03 | -0,04 | 0,8 | 0,15854 | 0,094242 | 0,088484 | 1,319256 |
| Вектор-столбец конечного использования | Вектор-столбец валового выпуска | ||||||
| 40,3 |
|
|
| 101,3527 |
|
|
|
| 21 |
|
|
| 45,95028 |
|
|
|
| 1,3 |
|
|
| 11,9743 |
|
|
|
| 2,5 |
|
|
| 11,78139 |
|
|
|
Рис. 10.6. Результат применения инструмента.
Реализация в MatLab. Вычисления в MatLab можно выполнить в командном окне Command Window, вводя и выполняя последовательно команды. Но предпочтительней создать m-файл . Он создается в специальном окне Editor (реактор m- файлов), которое вызывается командой File ® New ® M - File. Для сохранения созданного m-файла можно воспользоваться командой File ® Save As . Для выполнения набранной программы необходимо выполнить команду Run из меню Debug или нажать клавишу <F5>. Результаты выполнения программы или сообщения об ошибках отображаются в командном окне.
Для задания вектора-строки (матрицы-строки, т. е. матрицы 1´n) используют квадратные скобки, в которых числовые данные отделяются друг от друга запятыми иди пробелами. Для задания вектора-столбца (матрицы- столбца, т. е. матрицы n´1) используют также квадратные скобки, но в них числовые данные отделяются друг от друга точками с запятыми. Для формирования матрицы необходимо скомбинировать оба варианта. Так матрица A примера 10.1 представляется как двумерный массив:
A=[0.52 0.12 0.04 0.2; 0.07 0.35 0.03 0.12; 0.04 0.03 0.3 0.14; 0.05 0.03 0.04 0.2].
Для задания вектора Y можно сначала сформировать матрицу-строку
Y=[40.3 21 1.3 2.5], а затем транспонировать используя символ ¢.
Построим матрицу E-A. Для генерирования единичной матрицы воспользуемся функцией eye(n), где n - порядок единичной матрицы. Вычислить матрицу E-A можно, написав всего одну строку: eye(4)-A. Здесь знак минус (-) определяет покомпонентное вычитание двух массивов одинаковой размерности.
Нахождение обратной матрицы. Обратная матрица находится с помощью функции inv(). Таким образом, матрица B=(E-A)-1 может быть вычислена с использованием следующего кода: B=inv(eye(4)-A).
Символом умножения матриц является традиционный знак *.
Приведем программу для решения данной задачи.
A=[0.52 0.12 0.04 0.2; 0.07 0.35 0.03 0.12; 0.04 0.03 0.3 0.14; 0.05 . . . 0.03 0.04 0.2]; %задаются коэффициенты матрицы системы
Y=[40.3 21 1.3 2.5]; %задаются правые части матрицы системы
B=inv(eye(4)-A) %вычисляется обратная матрица
X=B*Y' %находится решение системы.
В результате выполнения программы в командном окне получим
B =
2.2331 0.4512 0.1846 0.6582
0.2777 1.6097 0.1037 0.3290
0.1712 0.1136 1.4613 0.3156
0.1585 0.0942 0.0885 1.3193
X =
101.3527
45.9503
11.9743
11.7814
По умолчанию MatLab выводит на экран числа в формате short – 4 знака после запятой. Здесь использована функция vpa(var,n) для вывода на экран n значащих цифр для переменной или массива var. Применим ее для вывода на экран элементов матрицы и вектора содержащих семь значащих цифр.
A=[0.52 0.12 0.04 0.2; 0.07 0.35 0.03 0.12; 0.04 0.03 0.3 0.14; 0.05 . . . 0.03 0.04 0.2];
Y=[40.3 21 1.3 2.5];
B=inv(eye(4)-A);
B=vpa(B,7) %выводится на экран обратная матрица
X=B*Y';
X=vpa(X,7) %выводится на экран решение системы
Теперь после выполнения программы получим следующий результат
B =
[ 2.233073, .4511577, .1845532, .6582387]
[ .2776558, 1.609690, .1036531, .3290067]
[ .1712117, .1136155, 1.461256, .3155651]
[ .1585397, .9424151e-1, .8848439e-1, 1.319256]
X =
101.3527
45.95028
11.97430
11.78139
Если использовать операцию левого матричного деления (символ \), то можно миновать операцию вычисления обратной матрицы и в этом случае программа примет следующий вид:
A=[0.52 0.12 0.04 0.2; 0.07 0.35 0.03 0.12; 0.04 0.03 0.3 0.14; 0.05 0.03 0.04 0.2];
Y=[40.3 21 1.3 2.5];
X=(eye(4)-A)\Y';
X=vpa(X,7)
Способ 2. Решение модели МОБ на основе решения системы одновременных линейных уравнений.
Реализация в Excel. Для решения системы линейных уравнений может быть использована команда Поиск решения из меню Сервис Excel, позволяющая решать оптимизационные задачи. Поскольку система n линейных уравнений с n неизвестными, при условии ее разрешимости, имеет единственное решение, то введение любой целевой функции не оказывает влияния на решение системы, т.к. область допустимых значений системы – единственная точка. Поэтому целевая функция имеет формальный характер и необходима лишь для того, чтобы активизировать команду Поиск решения.
Методику решения системы линейных уравнений продемонстрируем для рассмотренного примера:

или в развернутом виде:




Предварительно введем в таблицу Excel исходные данные задачи: будем предполагать, что переменные модели (  ) находятся соответственно в ячейках А1-D1. В ячейку А2 вводим левую часть первого ограничения:
) находятся соответственно в ячейках А1-D1. В ячейку А2 вводим левую часть первого ограничения:
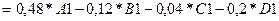 ,
,
А3 – левую часть второго ограничения:
 ,
,
А4 – третьего:
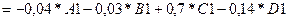 ,
,
А5 – четвертого:
 .
.
В ячейке А6 договоримся, что находится линейная функция любого вида, выраженная через переменные А1-D1, например:

Диалоговое окно ввода данных представлено на рис.10.7.

Рис.10.7. Подготовка данных для активизации инструмента Поиск решения.
Далее вызываем команду Поиск решения из меню Сервис, щелкнув М1 последовательно по их названиям (рис.10.8). На экране –

Рис.10.8. Диалоговое окно активизации инструмента Поиск решения.
диалоговое окно Поиск решения. В поле Установить целевую ячейку занесем название ячейки А6. После слова Равной можно выделять Максимальное значение или Минимальное значение – это не имеет значения, т.к. целевая функция в данном случае имеет формальный характер и не оказывает влияния на решение. Еще раз повторим, что целевая функция в данном случае должна быть выделена лишь для того, чтобы активизировать команду Поиск решения. В поле Изменяя ячейки: занесем диапазон переменных модели А1-D1, т.к. именно эти ячейки отведены под значения вычисляемых переменных, щелкнув М1 по красной стрелке в этом поле. Далее занесем ограничения задачи в поле Ограничения: для чего щелкнем М1 по кнопке Добавить. На экране диалоговое окно Добавление ограничения. В поле Ссылка на ячейку заносим ячейку А2, где располагается левая часть первого ограничения, в среднее поле занесем равенство, выделив его в открывшемся окне. В правое поле занесем правую часть первого ограничения - число 40,3. Далее занесем второе ограничение в поле Ограничения, для чего проделаем аналогичную процедуру со вторым ограничением, которое располагается в ячейке А3, в правой части равенства указываем значение 21. Аналогично для последующих третьего и четвертого ограничений. Так как все условия задачи введены, щелкнем М1 по ОК. На экране - диалоговое окно Поиск решения (рис.10.9).
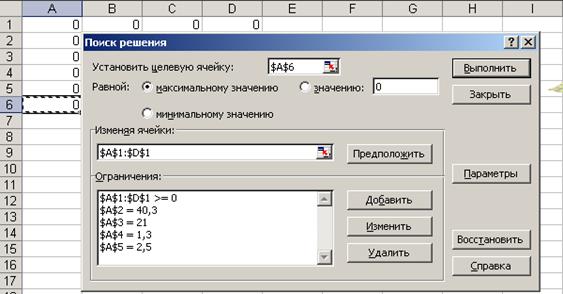
Рис.10.9. Диалоговое окно активизации инструмента Поиск решения.
Щелкнем М1 по кнопке Выполнить. На экране в ячейках А1-D1 полученные результаты решения (рис. 10.10): 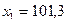 ,
,  ,
,  ,
,  .
.

Рис. 10.10. Результат применения инструмента.
Реализация в MatLab. В состав MatLab входит расширение Symbolic Math ToolBox, которое добавляет возможность символьных вычислений, в частности, решать системы линейных уравнений. Для решения систем уравнений применяется функция solve(expr1, expr2, … exprN , var1, var1, … varN). Функция возвращает значения переменных var1, var1, … varN, при которых выражения expr1, expr2, … exprN равны нулю или удовлетворяются равенства expr1, expr2, … exprN. Результат выполнения функции solve, записывается в рабочее пространство (Workspace ) в виде структуры с полями var1, var1, … varN, каждое из которых содержит символьное представление решения.
Для реализации символьных вычислений нужно создать символьные объекты. Для создания символьных объектов служит команда syms. После этого можно выполнять алгебраические преобразования над символьными объектами.
Приведем программу для решения системы линейных уравнений.
A=[0.52 0.12 0.04 0.2; 0.07 0.35 0.03 0.12; 0.04 0.03 0.3 0.14; 0.05 0.03 0.04 0.2];
Y=[40.3; 21; 1.3; 2.5];
B=eye(4)-A;
syms x1 x2 x3 x4 %создаются символьные объекты
X1=[x1; x2; x3; x4]; %создается вектор символьных объектов
b=B*X1-Y; %создаются левые части системы AX-Y=0 в символьном виде
vpa(b,7)
S=solve(b(1), b(2),b(3),b(4),x1, x2, x3, x4) %решается система уравнений
R=[S.x1,S.x2,S.x3,S.x4]; %формируется массив R, %представляющий решение системы уравнений
vpa(R,7)
Примеры построения моделей МОБ. Приведем примеры, иллюстрирующие алгоритм построения моделей, их решения и интерпретации.
Пример 10.4. Пусть технологические процессы в экономике описываются матрицей коэффициентов прямых затрат А из примера 10.3. Определить валовую продукцию отраслей при условии, что в прогнозном периоде выраженный в сопоставимых ценах конечный платежеспособный спрос на продукцию отраслей составит соответственно: 40,3 млрд. д.е., 21 млрд. д.е., 1,3 млрд. д.е.., 2,5 млрд. д.е. Дать экономический анализ полученного решения.
Решение. В задаче известны показатели конечного спроса на продукцию отраслей 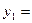 40,3,
40,3,  21,
21,  1,3,
1,3,  2,5, а также матрица прямых затрат А. При подстановке этих данных в базовую прогнозную модель вида (
2,5, а также матрица прямых затрат А. При подстановке этих данных в базовую прогнозную модель вида (  ), искомая система балансовых уравнений примет следующий вид:
), искомая система балансовых уравнений примет следующий вид:




 .
.
После решения системы уравнений получим:  101, 3,
101, 3,  46,
46,  12,
12,  11,8. Т.е. для обеспечения конечного спроса на продукцию отраслей
11,8. Т.е. для обеспечения конечного спроса на продукцию отраслей 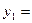 40,3 млрд.д.е.,
40,3 млрд.д.е.,  21 млрд.д.е.,
21 млрд.д.е.,  1,3 млрд.д.е.,
1,3 млрд.д.е.,  2,5 млрд.д.е. в рамках технологических процессов, описываемых матрицей прямых затрат А, необходимо обеспечить производство валового выпуска отраслей в сопоставимых ценах в объемах:
2,5 млрд.д.е. в рамках технологических процессов, описываемых матрицей прямых затрат А, необходимо обеспечить производство валового выпуска отраслей в сопоставимых ценах в объемах:  101, 3 млрд.д.е.,
101, 3 млрд.д.е.,  46 млрд.д.е.,
46 млрд.д.е.,  12 млрд.д.е.,
12 млрд.д.е.,  11,8 млрд.д.е.
11,8 млрд.д.е.
Пример 10.5. Пусть, в дополнение к условиям задачи 10.4, предполагается, что в прогнозном периоде конечный спрос на продукцию сельского хозяйства (отрасль 2) должен увеличиться на 30%, а в других отраслях останется неизменным. Как измениться модель МОБ. Дать экономический анализ полученного решения.
Решение. В задаче известны показатели конечного спроса на продукцию отраслей 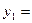 40,3,
40,3,  21*1,3=27,3,
21*1,3=27,3,  1,3,
1,3,  2,5, а также матрица прямых затрат А. После подстановки этих данных в базовую прогнозную модель вида (
2,5, а также матрица прямых затрат А. После подстановки этих данных в базовую прогнозную модель вида (  ), искомая система балансовых уравнений модели примет следующий вид:
), искомая система балансовых уравнений модели примет следующий вид:




 .
.
После решения системы уравнений получим: 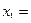 104, 2,
104, 2,  56,1
56,1  12,7
12,7  12,4.
12,4.
Если конечный спрос на продукцию сельского хозяйства увеличится на 30%, то, как показывает реализация модифицированной модели, объемы валовых выпусков в отраслях изменятся следующим образом: 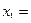 104,2 млрд.д.е.,
104,2 млрд.д.е.,  56,1 млрд.д.е.,
56,1 млрд.д.е.,  12,7 млрд.д.е.,
12,7 млрд.д.е.,  12,4 млрд.д.е. Сравнивая валовые выпуски промышленности в обоих случаях 104,2 млрд.д.е. и 101, 3 млрд.д.е. можно определить ожидаемый темп прироста производства промышленной продукции
12,4 млрд.д.е. Сравнивая валовые выпуски промышленности в обоих случаях 104,2 млрд.д.е. и 101, 3 млрд.д.е. можно определить ожидаемый темп прироста производства промышленной продукции  =2,9%, сельского хозяйства
=2,9%, сельского хозяйства  = 22%, прочих отраслей материального производства 5,8%, услуг 5%, который ожидается при условии неизменных технологических процессов.
= 22%, прочих отраслей материального производства 5,8%, услуг 5%, который ожидается при условии неизменных технологических процессов.
Пример 10.6. Пусть технологические процессы в экономике описываются матрицей коэффициентов прямых затрат А из примера 10.3. Построить модель для расчета ВВП при условии, что валовые выпуски отраслей в прогнозном периоде составят соответственно: 102 млрд. д.е., 57 млрд. д.е., 15 млрд. д.е., 20 млрд. д.е. Дать экономический анализ полученного решения.
Решение. В задаче известны показатели валового выпуска отраслей  102,
102,  57,
57,  15,
15,  20, а также матрица прямых затрат А. Подставляя эти данные в базовую прогнозную модель вида (
20, а также матрица прямых затрат А. Подставляя эти данные в базовую прогнозную модель вида (  ), получаем следующую систему балансовых уравнений модели:
), получаем следующую систему балансовых уравнений модели:





