 |
Главная |
Теорема 1. Формула Грина.
|
из
5.00
|
Пусть в области  , граница которого - замкнутый контур
, граница которого - замкнутый контур  , являющийся односвязным множеством, задано плоское векторное поле
, являющийся односвязным множеством, задано плоское векторное поле  .
.
Тогда верна такая формула:  .
.
То есть, работа силы по границе области равна двойному интегралу от величины  по этой плоской области.
по этой плоской области.
Доказательство (ДОК 1). Спроецируем область на ось Ох, обозначим границы проекции: точки  . Сама граница области тогда условно подразделяется на две линии, снизу
. Сама граница области тогда условно подразделяется на две линии, снизу  , а сверху
, а сверху  . Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по
. Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по  двигаться слева направо, а по
двигаться слева направо, а по  справа налево.
справа налево.

Рассмотрим подробнее интеграл от функции  по границе области. В соответствии со всем сказанным, он может быть записан так:
по границе области. В соответствии со всем сказанным, он может быть записан так:  . Но во втором интеграле можно изменить
. Но во втором интеграле можно изменить  на
на  , сменив знак.
, сменив знак.
 и их можно объединить
и их можно объединить
 =
= 
разность, которая внутри интеграла, является результатом применения формулы Ньютона-Лейбница по переменной  :
:
запишем это в виде:  .
.
Но если формула Ньютона-Лейбница применяется к  , значит,
, значит,  это первообразная по
это первообразная по  , а она очевидно, является первообразной от своей производной
, а она очевидно, является первообразной от своей производной 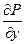 . То есть:
. То есть:
 =
=  а этой как раз и есть двойной интеграл по области D.
а этой как раз и есть двойной интеграл по области D.
 =
=  .
.
Аналогично можно спроецировать область D на ось Оу, допустим проекция займёт некоторый отрезок  . Левую и правую линии, составляющие замкнутый контур, обозначим
. Левую и правую линии, составляющие замкнутый контур, обозначим  и
и  . Правая здесь будет
. Правая здесь будет  (она дальше от оси Оу).
(она дальше от оси Оу).

Тогда  =
= 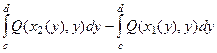 =
=  =
=
 =
= 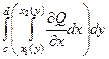 =
= 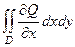 .
.
Сложим два полученных равенства и получается двойной интеграл
 .
.
Пример. Решим тот же самый пример, что рассматривали недавно, работа поля  при движении точки по единичной окружности, но сделаем это теперь по формуле Грина.
при движении точки по единичной окружности, но сделаем это теперь по формуле Грина.
 . Тогда
. Тогда  =
=  =
=  где D - круг радиуса 1. Тогда интеграл от 1 это его площадь.
где D - круг радиуса 1. Тогда интеграл от 1 это его площадь.  =
=  =
=  .
.
Потенциальные поля
Скалярное поле, или скалярная функция:  .
.
Векторная функция, которая отображает  называется векторным полем.
называется векторным полем.
Заметим, что градиент скалярной функции - это векторная функция:
 ,
,  ,
, 
То есть, по скалярному полю всегда можно построить некоторое векторное.
Пример:  . Тогда
. Тогда  .
.
Обратная задача: если даны некоторые 3 скалярные функции, т.е. векторное поле, всегда ли они являются частными производными какой-то единой скалярной функции? Оказывается, нет.
Определение. Если существует такая скалярная функция  , что выполняется
, что выполняется  ,
,  ,
,  , (то есть их общая первообразная), то векторное поле называется потенциальным, а функция
, (то есть их общая первообразная), то векторное поле называется потенциальным, а функция  называется потенциалом поля
называется потенциалом поля  .
.
Кстати, если  - потенциал, то
- потенциал, то 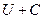 - тоже потенциал, ведь
- тоже потенциал, ведь  ,
,  ,
, 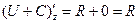 .
.
Потенциал определяется с точностью до константы (точно так же как и первообразная). Именно поэтому в физике важна именно разность потенциалов, а не сам потенциал.
Примеры.
Пример не потенциального поля.
 . Первообразная от 1 компоненты по
. Первообразная от 1 компоненты по  это
это 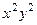 , однако первообразная по
, однако первообразная по  от второй компоненты совсем другая:
от второй компоненты совсем другая:
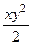 , они не совпадают.
, они не совпадают.
Пример потенциального поля.
 . Его потенциал:
. Его потенциал:  .
.
Далее нам надо научиться выяснять 2 вопроса:
1) выяснять, является ли поле потенциальным.
2) вычислять потенциал, если оно потенциально.
Теорема 2. Криволинейный интеграл 2 рода не зависит от пути  циркуляция по замкнутому контуру равна 0.
циркуляция по замкнутому контуру равна 0.
|
из
5.00
|
Обсуждение в статье: Теорема 1. Формула Грина. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

