 |
Главная |
Доказательство. (ДОК 12).
|
из
5.00
|
Запишем 2 условия Коши-Римана. Одно продифференцируем по переменной 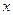 , а второе по
, а второе по  :
:




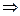
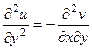 .
.
Сложим теперь эти 2 равенства, но при этом смешанные производные 2 порядка от  при этом совпадают, они вычитаются и дают 0.
при этом совпадают, они вычитаются и дают 0.
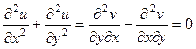 . Итак,
. Итак,  .
.
Теперь снова запишем условия Коши-Римана, 1-е дифференцируем по  , а второе по
, а второе по 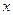 .
.

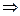



 .
.
Теперь вычтем из 1-го равенства 2-е.
 , тогда
, тогда  .
.
ЛЕКЦИЯ 4. 23.09.2019
Пример.  =
=  . Здесь для
. Здесь для  не верно уравнение Лапласа:
не верно уравнение Лапласа: 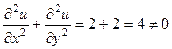 .
.
Пример.  =
=  . Уравнение Лапласа для обеих частей функции:
. Уравнение Лапласа для обеих частей функции:
1)  ,
, 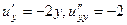 , в сумме 0.
, в сумме 0.
2) 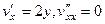 ,
, 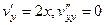 , 0+0=0.
, 0+0=0.
Теорема 4. Условия Коши-Римана эквивалентны условию  .
.
Доказательство (ДОК 13). Вспомним, что  можно выразить через
можно выразить через  таким образом:
таким образом: 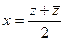 ,
,  . Сделаем это в функциях
. Сделаем это в функциях  .
.
 =
=  .
.
Таким образом, функция стала выражена через два аргумента 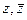 , а значит, можно искать частную производную по
, а значит, можно искать частную производную по  .
.
Вспомним формулу полной производной (из 1 семестра) для случая композиции типа  :
:  . Найдём производные от
. Найдём производные от  по
по  этим методом, причём здесь тоже промежуточные переменные
этим методом, причём здесь тоже промежуточные переменные  .
.
 ,
,  .
.
При этом такие компоненты как  и
и  можно найти
можно найти
из формул  ,
,  , а именно :
, а именно :
 =
= 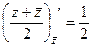 ,
,  =
=  . Таким образом,
. Таким образом,
 ,
,  .
.
Тогда  =
=  =
=
 =
=  =
=
 =
=  .
.
Выполнение условий Коши-Римана 

в данном случае как раз и эквивалентно тому, что в обеих скобках нули, то есть  .
.
□
Итак, как видим, наличие  в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии
в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии  или
или 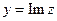 , в составе которых есть элемент
, в составе которых есть элемент  .
.
Алгоритм восстановления аналитической функции по её действительной или мнимой части.
Поскольку действительная и мнимая части взаимосвязаны условиями Коши-Римана, то достаточно одной её части, чтобы восстановить вторую часть, и далее всю функцию  .
.
Например, нам известна  . Тогда
. Тогда  =
=  , это криволинейный интеграл 2 рода для векторного поля
, это криволинейный интеграл 2 рода для векторного поля 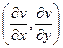 от фиксированной точки, например (0,0) до произвольной
от фиксированной точки, например (0,0) до произвольной  . Нам неизвестны эти частные производные, как и сама функция
. Нам неизвестны эти частные производные, как и сама функция 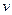 , однако их можно заменить на известные, по условиям Коши-Римана.
, однако их можно заменить на известные, по условиям Коши-Римана.
 =
=  и далее вычислить.
и далее вычислить.
Итак, алгоритм:
1. Проверить выполнение уравнения Лапласа (иначе  или
или 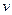 не может быть частью какой-то единой комплексной функции).
не может быть частью какой-то единой комплексной функции).
2. Вычислить криволинейный интеграл.
3. В полученной функции  выразить
выразить  по формулам:
по формулам: 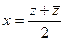 ,
,  . При правильном вычислении сократятся все
. При правильном вычислении сократятся все  и останется только
и останется только  .
.
Пример. Дано  . Узнать мнимую часть и восстановить вид функции
. Узнать мнимую часть и восстановить вид функции  .
.
Сначала проверяем уравнение Лапласа.
 ,
,  , сумма 2-й производных равна 0, то есть
, сумма 2-й производных равна 0, то есть  является одной из компонент комплексной функции.
является одной из компонент комплексной функции.
 =
=  =
=  , где
, где  .
.
Итак, найдём криволинейный интеграл 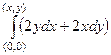 . Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля.
. Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля.  =
=  =
=  .
.
Далее, в выражение  подставим
подставим  ,
, 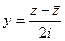 .
.
 =
=  =
=
 =
=  =
=  =
=  . Итак,
. Итак,  .
.
|
из
5.00
|
Обсуждение в статье: Доказательство. (ДОК 12). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

