 |
Главная |
Доказательство (ДОК 4).
|
из
5.00
|
1) Необходимость. Пусть поле потенциально. Тогда 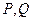 являются производными от какой-то общей функции
являются производными от какой-то общей функции  , т.е.
, т.е.  ,
,  . тогда
. тогда  ,
,  . Но смешанные частные производные 2-го порядка совпадают, значит,
. Но смешанные частные производные 2-го порядка совпадают, значит,  =
=  .
.
а следовательно, 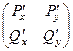 =
= 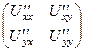 .
.
2) Достаточность. Здесь мы будем использовать формулу Грина, которую доказали ранее, а там фактически неявно это и предполагали при записи двойного интеграла, когда для 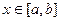 рассматривался отрезок
рассматривался отрезок  , то есть такая ситуация, как для кольца, не рассматривается, а только множества без внутренних пустот.
, то есть такая ситуация, как для кольца, не рассматривается, а только множества без внутренних пустот.
Если производная матрица симметрична, то  (в других обозначениях
(в других обозначениях  =
=  ). Тогда
). Тогда 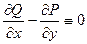 , и двойной интеграл по любой плоской области равен 0:
, и двойной интеграл по любой плоской области равен 0:  .
.
Но ведь тогда для любого замкнутого контура получается, что по формуле Грина, если двойной интеграл по его внутренней области 0, то и циркуляция по границе тоже 0:
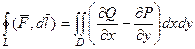 = 0,
= 0,
а если для любого контура циркуляция 0, то поле потенциально, что следует из теорем 1 и 2, доказанных ранее.
В 3-мерном случае требуется совпадение трёх пар производных, доказательство показано пока для 2-мерного случая, чтобы использовать формулу Грина.
Алгоритм нахождения потенциала.
1. Выяснить потенциальность поля, проверив симметричность производной матрицы (она сотоит из всех частных производных: от всех компонент векторного поля по всем переменным).
2. Найти потенциал, как скалярную функцию, равную криволинейному интегралу от фиксированной точки до произвольной.
Как правило, в качестве «начальной» фиксированной точки рассматривают начало координат, если же в функциях присутствуют к примеру  или
или  , то можно взять в качестве начальной точку (1,1) а не (0,0).
, то можно взять в качестве начальной точку (1,1) а не (0,0).
Путь от начальной точки до может быть по любой кривой, но практически лучше по ломаной, состоящей из отрезков, параллельных осям координат. Сначала от (0,0) к (x,0) а затем 2-е звено до точки (x,y).

Пример. Доказать, что поле  потенциально и найти потенциал.
потенциально и найти потенциал.
Решение. Шаг 1. Сначала найдём производную матрицу, вычислив все частные производные по всем переменным:
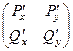 =
= 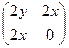 . Мы видим, что она симметрична. Значит, поле потенциально.
. Мы видим, что она симметрична. Значит, поле потенциально.
Шаг 2. Найдём криволинейный интеграл от (0,0) до  , соединив с помощью ломаной. Лучше всего даже обозначить конечную точку
, соединив с помощью ломаной. Лучше всего даже обозначить конечную точку  , чтобы не путать обозначение переменной, по которой ведётся интегрирование, и верхнего предела. Вычислив
, чтобы не путать обозначение переменной, по которой ведётся интегрирование, и верхнего предела. Вычислив 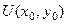 , затем мы учтём тот факт, что эта точка была произвольной, и сможем записать уже просто
, затем мы учтём тот факт, что эта точка была произвольной, и сможем записать уже просто  .
.
 разбивается на сумму двух интегралов, по каждому участку ломаной, причём на каждом из них обнуляется один из двух дифференциалов: на горизонтальном отрезке меняется только
разбивается на сумму двух интегралов, по каждому участку ломаной, причём на каждом из них обнуляется один из двух дифференциалов: на горизонтальном отрезке меняется только  , а тогда
, а тогда  , на вертикальном меняется
, на вертикальном меняется  , тогда
, тогда  .
.
 =
= 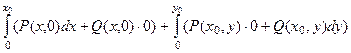
в обоих интегралах формально присутствуют оба слагаемых, но одно из них обнуляется, поэтому выглядит далее так, как будто распределилось по одному слагаемому в каждый интеграл.
 в первом фиксировано
в первом фиксировано  , а на втором участке переменная
, а на втором участке переменная  уже достигла
уже достигла  и далее не меняется, поэтому там
и далее не меняется, поэтому там  .
.
Для данного конкретного примера получается
 =
=  =
=  =
=  .
.
Итак,  , тогда можно сказать, что
, тогда можно сказать, что  .
.
Проверка.  ,
,  .
.
Глава 2.
|
из
5.00
|
Обсуждение в статье: Доказательство (ДОК 4). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

