 |
Главная |
Биномиальное распределение.
|
из
5.00
|
На практике оно возникает при следующих условиях. Проводится  независимых испытаний. В каждом из опытов, событие А может появиться с вероятностью p и не появится с вероятностью
независимых испытаний. В каждом из опытов, событие А может появиться с вероятностью p и не появится с вероятностью  .
.
Вероятность того что событие  появиться ровно
появиться ровно  раз в серии из
раз в серии из  опытов вычисляют по формуле Бернулли
опытов вычисляют по формуле Бернулли
 , где
, где  ;
;
m = 0,1, 2,… n (9)
Такое распределение называют биномиальным. Биномиальное распределение имеет вид, представленный в таблице 4:
Таблица 4 – Закон распределения вероятностей в случае 1.2.2
| Х | 0 | 1 | 2 | … | m | … | n |
| P | 
| 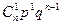
| 
| 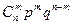
| 
|
Доказано, что для биномиального распределения
 ;
;  ;
;  . (10)
. (10)
Обратимся к примеру 1. Поскольку вероятность появления каждого значения случайной величины Х определяется по формуле Бернулли, то имеет место биномиальное распределение. Тогда математическое ожидание и дисперсию можно вычислить по формулам (10):
М(Х) = 2 · 0,89 = 1,78; D(X) = 2 · 0,89 · 0,11 = 0,1958.
Результаты вычисления по формулам (4), (6), и (7) совпадают с результатами вычисления по формулам (10). Поэтому в данном распределении для вычисления выбираем более простые формулы (10).
Распределение Пуассона.
При больших значениях  и малых значениях р (пишут:
и малых значениях р (пишут:  ;
;  ) вычисление по формуле Бернулли становится весьма затруднительным и тогда применяют приближенную формулу Пуассона
) вычисление по формуле Бернулли становится весьма затруднительным и тогда применяют приближенную формулу Пуассона
 , где a = n p; m = 0,1, 2 …n,… (11)
, где a = n p; m = 0,1, 2 …n,… (11)
Это распределение зависит только от одного параметра  , что является преимуществом закона Пуассона. Распределение Пуассона представлено в таблице 5.
, что является преимуществом закона Пуассона. Распределение Пуассона представлено в таблице 5.
Таблица 5 – Закон распределения вероятностей в случае 1.2.3
| Х | 0 | 1 | 2 | … | m | … |
| Р | 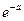
| 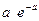
| 
| … | 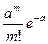
| … |
Применение формулы Пуассона оправдано, если  , иначе она дает большую погрешность.
, иначе она дает большую погрешность.
Пример 2
В банк было доставлено 2000 пакетов с денежными знаками. Вероятность несовпадения наличной денежной массы с документальной по каждому пакету равна 0,001. Составить закон распределения случайной величины Х - числа пакетов с денежной наличностью, несоответствующей документам и построить многоугольник распределения и функцию F(x) (ограничившись 5-тью случаями). Найти M(x), D(x),  (x).
(x).
Решение
Возможно, что несовпадение не обнаружится вовсе или обнаружится в одном пакете, двух, трёх и т.д. Поскольку п - велико, а р - мало, то вероятности этих значений посчитаем по формуле Пуассона. Пусть значения m изменяются от 0 до 5. Найдем параметр а. Он будет равен:
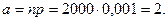
Распределение в случае  представлено в таблице 5а.
представлено в таблице 5а.
Таблица 5а – Закон распределения вероятностей в примере 2.
| Х | 0 | 1 | 2 | 3 | 4 | 5 |
| Р | 

|  =0,27
=0,27
| 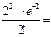 =0,27 =0,27
| 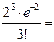 =0,18 =0,18
|  =0,09 =0,09
| 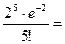 =0,036 =0,036
|
На рисунке 3 изображен многоугольник распределения в случае  .
.
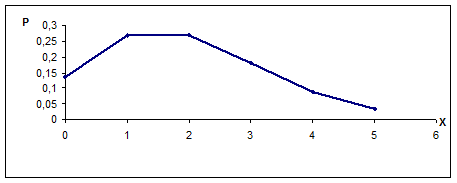 Рисунок 3 – Многоугольник распределения вероятностей в примере 2
Рисунок 3 – Многоугольник распределения вероятностей в примере 2
Очевидно, что значения функции F(х) будут на каждом последующем шаге вычисления приближаться к единице, достигая её лишь в пределе при 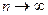 .
.

В пуассоновском распределении М (Х)= D(Х)=а=пр. (12)
В этом примере М (Х)= D(Х)=2.
|
из
5.00
|
Обсуждение в статье: Биномиальное распределение. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

