 |
Главная |
Основные законы распределения дискретной случайной величины
|
из
5.00
|
ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Методические указания и задания
для модульного контроля и практических занятий
по дисциплине
«Теория вероятностей и математическая статистика»
для студентов экономических спеціальностей
дневной формы обучения
Севастополь
2010
УДК 519.24
Теория вероятностей. Случайные величины. Методические указания и задания для модульного контроля и практических занятий по дисциплине «Теория вероятностей и математическая статистика» / Разраб. Л.Т. Потепалова.- Севастополь: Изд-во СевНТУ, 2010. – 60 с.
Методические указания предназначены для студентов экономических специальностей дневной формы обучения. Пособие содержит 30 вариантов заданий, охватывающих такие разделы дисциплины как случайные величины, основные законы их распределения и двумерные случайные величины. В методических указаниях приведены подробные решения типовых задач и теоретические сведения, приведен список учебной литературы, необходимой для углубленного изучения предмета.
Методические указания могут быть использованы студентами других специальностей и форм обучения.
Варианты заданий могут быть использованы как для модульного контроля, так и для практических занятий.
Методические указания рассмотрены и утверждены на заседании кафедры высшей математики, протокол № 2
от 28 сентября 2010 г.
Рецензент: Ледяев С.Ф., доцент кафедры высшей математики, кандидат технических наук
СОДЕРЖАНИЕ
1 ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ………………………...4
1.1 Основные понятия и вероятностные характеристики……………4
1.2 Основные законы распределения дискретной случайной величины…………………………………………………………………..9
1.2.1 Равномерное распределение…………………………………...9
1.2.2 Биномиальное распределение………………………………….9
1.2.3 Распределение Пуассона……………………………………...10
1.2.4 Геометрическое распределение………………………………13
1.2.5 Урезанное геометрическое распределение…………………..14
1.2.6 Гипергеометрическое распределение………………………..15
2 НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ……………………..16
2.1 Основные понятия и вероятностные характеристики…………..16
2.2 Равномерное распределение……….……………………...............21
2.3 Нормальное распределение……………………………….............24
2.4 Показательное распределение………………………….…………29
3 ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА……..…………………..31
3.1 Основные понятия и вероятностные характеристики…………..31
3.2 Коэффициент корреляции………………………………………...36
4 ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ…………………………………...41
4.1 Дискретная случайная величина………………………….............41
4.2 Непрерывная случайная величина……………………………......45
4.3 Нормальное распределение……………………………….............49
4.4 Равномерное и показательное распределения…………………...50
4.5 Двумерная случайная величина…………………………………..51
Приложение А…………………………………………………………..56
Приложение Б…………………………………………………………..57
Приложение В…………………………………………………………..58
Библиографический список……………………………………………60
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной величиной называется величина, которая в результате испытания примет одно и только одно возможное значение, заранее неизвестное.
Случайные величины обозначают большими буквами: X, Y, Z и др.
Различают дискретные случайные величины и непрерывные случайные величины.
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Основные понятия и вероятностные характеристики
Случайная величина X, принимающая конкретные числовые значения x i с вероятностью 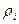 называется дискретной случайной величиной.
называется дискретной случайной величиной.
Законом распределения вероятностей называют последовательность (конечную или бесконечную) возможных значений случайной величины и соответствующих им вероятностей.
Простейшей формой задания закона распределения является таблица 1.
Таблица 1 – Закон распределения дискретной случайной величины
| Возможные значения случайной величины X | 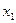
| 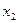
| … | 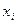
| … |
| Вероятности P, соответствующие этим значениям | p1 | p2 | … | pi | … |
Эту таблицу называют рядом распределения случайной величины. Графическое представление ряда распределения называется многоугольником распределения. Он дает наглядное приближенное представление о характере распределения случайной величины Х. Для его построения по оси ОХ откладывают значения случайной величины Х, а по оси ОУ соответствующие вероятности (рисунок 1).
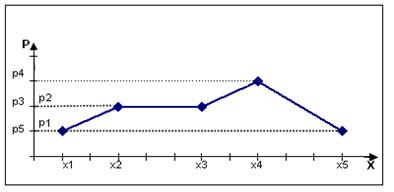
Рисунок 1 – Многоугольник распределения вероятностей.
Тот факт, что случайная величина Х в результате опыта обязательно примет одно из своих возможных значений 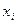 является достоверным событием, поэтому
является достоверным событием, поэтому 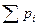 =1. Случайную величину Х можно задать и с помощью функции распределения.
=1. Случайную величину Х можно задать и с помощью функции распределения.
Функцией распределения случайной величины X называется функция F( x), выражающая вероятность того, что X примет значение меньшее, чем x:
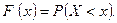 (1)
(1)
Для дискретной случайной величины функция распределения может быть найдена по формуле:
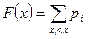 . (2)
. (2)
Вероятность того, что случайная величина X принимает значение в заданном числовом промежутке (а, b) определяется равенством:
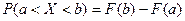 . (3)
. (3)
Характеристикой среднего значения случайной величины Х, около которого группируются все её возможные значения ,является математическое ожидание. Его обозначают М(X) или mх. Математическим ожиданием дискретной случайной величины X или её средним значением называется сумма произведений её возможных значений на соответствующие им вероятности:
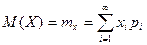 . (4)
. (4)
Характеристикой рассеяния возможных значений случайных величин вокруг математического ожидания служит дисперсия. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания: 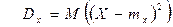 . (5)
. (5)
Дисперсия определяется равенством:
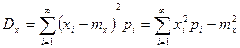 . (6)
. (6)
Дисперсия имеет размерность квадрата случайной величины, что не позволяет указать её на оси случайной величины, поэтому в качестве показателя рассеяния используют так же величину 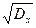 , размерность которой аналогична размерности случайной величины Х. Средним квадратическим отклонением дискретной случайной величины Х называется корень квадратный из дисперсии:
, размерность которой аналогична размерности случайной величины Х. Средним квадратическим отклонением дискретной случайной величины Х называется корень квадратный из дисперсии:
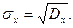 (7)
(7)
Все свойства математического ожидания, дисперсии и среднего квадратического отклонения для дискретных случайных величин переносятся и на случай непрерывных случайных величин.
Пример 1.
Оптовая база закупает компьютеры в равных количествах у трех производителей. Вероятность того, что компьютеры отличного качества для каждой фирмы соответственно равна 0,84; 0,9; 0,93. Составить закон распределения количества компьютеров отличного качества среди купленных двух. Построить многоугольник распределения такой случайной величины Х.
Решение
Вероятность покупки компьютера отличного качества определим по формуле полной вероятности:
р = 0,84 · 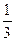 + 0,9 ·
+ 0,9 · 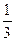 + 0,93 ·
+ 0,93 · 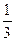 = 0,89.
= 0,89.
Среди купленных двух (n = 2) могут быть два отличного качества или один, или ни одного. Это значения случайной величины Х. Вероятности просчитаем по формуле Бернулли.
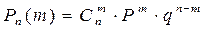 .
.
Р2(0) = С 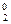 · 0,89
· 0,89 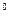 · 0,112 = 0,0121; P2(1) = C
· 0,112 = 0,0121; P2(1) = C 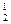 · 0,89 · 0,11 = 0,1958;
· 0,89 · 0,11 = 0,1958;
P2(2) = C 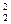 · 0,892 · 0,110 = 0,7921.
· 0,892 · 0,110 = 0,7921.
Проверим правильность составления закона распределения. Сумма этих вероятностей должна быть равной единице.
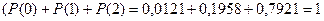 .
.
Тогда ряд и многоугольник распределения будут иметь вид, представленный таблицей 2 и рисунком 2 соответственно.
Таблица 2 – Закон распределения в примере 1
| Х | 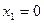
| 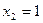
| 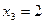
|
| Р | 0,0121 | 0,1958 | 0,7921 |
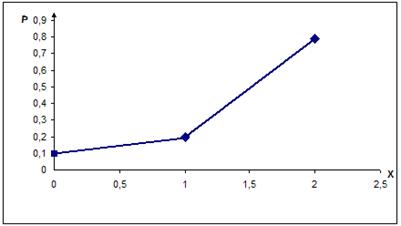
Рисунок 2 – Многоугольник распределения вероятностей в примере 1
Построим функцию распределения для данной случайной величины:
 F(x) =
F(x) = 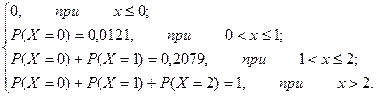
Построим график функции распределения. Он будет иметь вид, представленный на рисунке 2а.
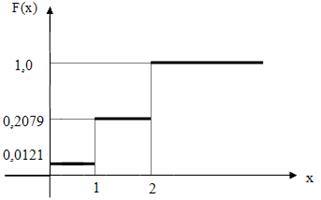
Рисунок 2а – Функция распределения в примере 1.
Таким образом, график функции распределения дискретной случайной величины имеет разрывы с конечным скачком (величиной равной вероятности pi ) в точках, где случайная величина принимает свои значения xi .
Найдем числовые характеристики рассматриваемой случайной величины: М(Х), D(Х), s (Х).
М(Х) = 0·0,0121 + 1·0,1958 + 2·0,7921 = 0,1958 + 1,5842 = 1,78.
D(Х) = 02·0,0121 + 12·0,1958 + 22·0,7921 – 1,782 = 0,1958 + 3,1684 – 3,1684 = 0,1958.
s(Х) = 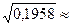 0,44.
0,44.
Основные законы распределения дискретной случайной величины
1.2.1 Равномерное распределение.
Равномерное распределение имеет дискретная случайная величина Х если:
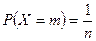 , m =1, 2, … n. (8)
, m =1, 2, … n. (8)
Распределение вероятностей имеет вид, представленный в таблице 3.
Таблица 3 – Закон распределения вероятностей в случае 1.2.1
| Х | 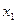
| 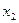
| … | 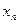
|
| Р | 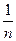
| 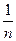
| … | 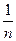
|
|
из
5.00
|
Обсуждение в статье: Основные законы распределения дискретной случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

